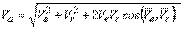Теорема о скоростях точек плоской фигуры.

Плоское (плоскопараллельное) движение твердого тела − это движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости.

Теорема.Скорость любой точки тела при плоском движении находится как сумма скорости полюса 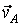и скорости данной точки во вращательном движении вокруг полюса :

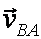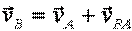
Было отмечено, что движение плоской фигуры можно рассматривать как слагающееся из поступательного движения, при котором все точки фигуры движутся со скоростью 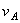полюса А, и из вращательного движения вокруг этого полюса. Покажем, что скорость любой точки М фигуры складывается геометрически из скоростей, которые точка получает в каждом из этих движений.

В самом деле, положение любой точки М фигуры определяется по отношению к осям Оху радиусом-вектором 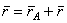(рис.30), где 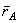- радиус-вектор полюса А, 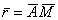- вектор, определяю­щий положение точки М относительно осей 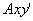, перемещающих­ся вместе с полюсом А поступательно (движение фигуры по отноше­нию к этим осям представляет собой вращение вокруг полюса А). Тогда

.

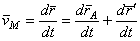В полученном равенстве величина 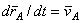есть скорость полюса А; величина же 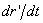равна скорости 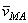, которую точка М получает при 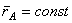, т.е. относительно осей , или, иначе говоря, при вращении фигуры вокруг полюса А. Таким образом, из предыдущего равенства действительно следует, что

.

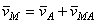Скорость 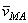, которую точка М получает при вращении фигуры вокруг полюса А:

,

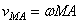
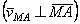где 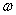- угловая скорость фигуры.

Таким образом, скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление скорости находятся построением соответствующего параллело­грамма (рис.31).

40.

41. 41 Условия равновесия плоской системы сил

Необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента. Для плоской системы сил эти условия получают вид F_o=åF_k=0, М_Оz=åМ_oz(F_k)=0, (5.15), где О– произвольная точка в плоскости действия сил. Получим: F_ox=åF_kx=F_1x+F_2x+…+F_nx=0, P_ox=åF_ky=F_1y+F_2y+…+F_ny=0, М_Оz=åM_Oz(F_k)=M_oz(F₁)+M_oz(F₂)+…+M_oz(F_n)=0, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой; åM_Az(F_k)=0, åM_Bz(F_k)=0, åM_Cz(F_k)=0, (5.17), где A, В и С– указанные точки. Необходимость выполнения этих равенств вытекает из условий (5.15). Докажем их достаточность. Предположим, что все равенства (5.17) выполняются. Равенство нулю главного момента при центре приведения в точке А возможно, либо если система приводится к равнодействую­щей (R≠0) и линия ее действия проходит через точку А, либо R=0; аналогично равенство нулю главного момента относительно точек В и С означает, что либо R≠0 и равнодействующая проходит через обе точки, либо R=0. Но равнодействующая не может про­ходить через все эти три точки А, В и С (по условию они не лежат на одной прямой). Следовательно, равенства (5.17) возможны лишь при R=0, т. е. система сил находится в равновесии. Заметим, что если точки А, В и С лежат на одной прямой, то выполнение условий (5.17) не будет достаточным условием равнове­сия, — в этом случае система может быть приведена к равнодейст­вующей, линия действия которой проходит через эти точки.

42\ пара сил и момент силы

Две параллельные силы, равные по величине и направленные в противоположные стороны, называются парой сил (фиг.30, а). Расстояние d между линиями действия сил пары называется плечом пары. Пару сил нельзя заменить и уравновесить одной силой. Уравновесить пару сил можно только другой парой. Пара сил, при­ложенная к твердому телу, вызывает его вращение, характеризую­щееся моментом пары. Моментом пары сил называется взятое со знаком (+) или (-) произведение величины одной из сил на ее плечо: m = ±Pd. Момент пары считается положительным, если пара стремится вращать тело против вращения часовой стрелки. Пару сил принято изображать изогнутой стрелкой (фиг.30, б). Буква у конца стрелки обозначает момент пары. Условие равновесия пар: для равновесия нескольких пар необхо­димо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

43)абсолютное движение — это движение точки/тела в базовой СО.

относительное движение — это движение точки/тела относительно подвижной системы отсчёта.

переносное движение — это движение подвижной СО всеми неизменно связанными с нею точками пространства относительно неподвижной СО.

Зависимость между абсол относит и переносной скоростями точки при сложном движении устанавливает ТЕОРЕМА о сложении скоростей

теорема о сложении скоростей: абсолютная скорость точки равна геометрической сумме переносной и относительной скоро­стей

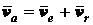
где 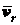- относительная скорость. 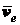- переносная скорость

Модуль определяем по теореме косинусов