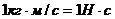Теорема об изменении кинетической энергии материальной точки.

Для доказательства теоремы запишем дифференциальное уравнение движения точки в виде mdV / dt = F. Умножая обе части уравнения скалярно на вектор элементарного действительного перемещения точки dr и учитывая, что dr / dt = V, имеем

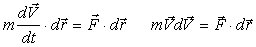(1)

Зная, что F - равнодействующая сил, приложенных к точке, обозначим δA скалярное произведение в правой части и назовем его элементарной работой сил, приложенных к точке:

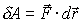(2)

Находя дифференциал от mV² / 2, имеем

Подставляя последнее выражение и выражение (2) в уравнение (1), получаем математическую запись теоремы в дифференциальной форме:

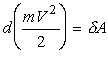(3)

Половину произведения массы точки на квадрат ее скорости под знаком дифференциала в левой части уравнения (3) называют кинетической энергией точки.

Это замечание позволяет по математической записи сформулировать теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал от кинетической энергии материальной точки равен элементарной работе сил, приложенных к точке.

Отметим, что кинетическая энергия - это еще одна, но уже скалярная, мера движения материальной точки, что дает ей определенные преимущества перед векторными мерами движения - количеством движения и моментом количества движения. В системе СИ единицей измерения кинетической энергии является джоуль, 1 Дж = кг·(м²/с²) = (кг·м/c²)·м = 1 Н·м.

Предположим, что при переходе точки из начального положения M₀ в конечное (или текущее) положение M ее скорость изменилась от начального значения V₀ до текущего (или конечного) значения V, и при этих предположениях проинтегрируем выражение (3). Тогда

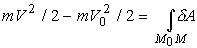
Интеграл в правой части этого выражения обозначим A и назовем полной работой или просто работой сил, приложенных к материальной точке:

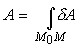(4)

Учитывая введенное обозначение, получаем математическую запись теоремы об изменении кинетической энергии материальной точки в интегральной форме:

mV2 / 2 - mV02 / 2 = A

(5)

то есть: изменение кинетической энергии материальной точки при ее переходе из начального положения в текущее (или конечное) положение равна работе сил, приложенных к точке, совершенной при этом переходе.

Теорема в интегральной форме в основном применяется, когда интеграл в правой части можно взять и вычислить полную работу сил. Тогда можно найти соотношение между перемещением и скоростью материальной точки. Теорема в дифференциальной форме удобна для составления дифференциальных уравнений движения материальной точки.

При практическом применении теоремы вычисление кинетической энергии точки обычно не вызывает трудностей, нужно только помнить о том, что ее нужно вычислять в абсолютном движении. Основной интерес и трудности представляют выражение элементарной работы и вычисление работы.

16.Количество движения точки

Количеством движения материальной точки 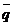называется вектор, равный произведению массы точки 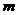на ее скорость .

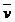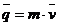
Количество движения точки в физике часто называютимпульсом материальной точки.

Проекции количества движения точки на прямоугольные декартовы оси координат равны:

, ,

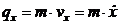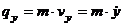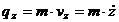
Единицей измерения количества движения в СИ является –