Свойства ковариационной матрицы

1. Ковариационная матрица является симметричной.

2. На главной диагонали ковариационной матрицы стоят дисперсии ком-

понент p -мерной случайной величины.

3. Ковариационная матрица является положительно определенной.

Наряду с ковариационной матрицей p -мерной случайной величины час-

то рассматривают её корреляционную матрицу.

Определение 7.11. Корреляционная матрица p -мерной случайной величины – квадратная матрица порядка p , составленная из коэффициен-

тов корреляций всевозможных пар компонент этой величины:

⎛ 1 r12

⎜

K r1 p ⎞

⎟

⎜r21

R = ⎜

1 K r2 p ⎟

⎠

⎟, где

rij

= ρ(X i , X j ).

⎜ M M O M ⎟

r

⎜

⎝ p1

rp 2 K ⎟

Определение 7.12. Говорят, что p -мерная случайная величина

X = (X1 , X 2 ,...,X p )

распределена по многомерному нормальному закону,

если её плотность вероятности имеет вид:

f ( X ) =

1

(2π) p ⋅det S

− 1 ( X −µ )⋅S −1 ⋅( X −µ )T

⋅e 2 ,

где µ – математическое ожидание, S – ковариационная матрица p -мерной

случайной величины X .

Замечание. Можно доказать, что если p -мерная случайная величина распределена по многомерному нормальному закону, то каждая ее компонента имеет нормальное распределение. Обратное утверждение, вообще говоря,

неверно.

Пример 7.1. Двумерная случайная величина задана законом распреде-

ления:

Y X
	0,1	0,2	0,1
	0,3	0,1	0,2

Найдите: a) законы распределения компонент X и Y , а также их числовые характеристики; б) условный закон распределения величины Y при условии

X =1; в) ковариационную и корреляционную матрицы двумерной случай-

ной величины ( X , Y ).

Y p 0,4 0,3 0,3

Решение. Законы распределения компонент имеют вид:

X
p	0,4	0,6

Найдем теперь числовые характеристики X и Y :

M ( X ) =1⋅0,4 + 2 ⋅0,6 =1,6 ;

M ( X 2 ) =12 ⋅0,4 + 22 ⋅0,6 = 2,8 ;

D( X ) = M ( X 2 ) −(M ( X ))2 = 0,24 ;

σ( X ) =

0,24 = 0,49 .

M (Y ) = 0 ⋅0,4 +1⋅0,3 + 2 ⋅0,3 = 0,9 ;

M (Y 2 ) = 02 ⋅0,4 +12 ⋅0,3 + 22 ⋅0,3 =1,5 ;

D(Y ) = M (Y 2 ) −(M (Y ))2 =1,35 ;

σ(Y ) =

1,35 =1,16 .

Составим теперь условный закон распределения величины Y при усло-

вии

X =1. Для этого найдем вероятности:

PX =1 (Y = 0) =

P(( X

=1)(Y = 0))

=

0,1

= 0,25 ;

P( X

= 1)

0,4

PX =1 (Y =1) =

P(( X

=1)(Y =1))

=

0,2

= 0,5 ;

P( X

= 1)

0,4

PX =1 (Y = 2) =

P(( X

=1)(Y = 2))

=

0,1

= 0,25 .

P( X

= 1)

0,4

Таким образом, условный закон распределения величины Y при условии

X =1:

Y
p	0,25	0,5	0,25

Для определения ковариационной матрицы вычислим

M ( X ⋅Y ) :

M ( X ⋅Y ) =1⋅0 ⋅0,1 +1⋅1⋅0,2 +1⋅2 ⋅0,1 + 2 ⋅0 ⋅0,3 + 2 ⋅1⋅0,1 + 2 ⋅2 ⋅0,2 =1,4 .

Таким образом, ковариация случайных величин X и Y равна

K ( X , Y ) = M ( X ⋅Y ) − M ( X ) ⋅ M (Y ) =1,4 −1,6 ⋅0,9 = −0,04 ,

следовательно, ковариационная матрица имеет вид

⎜

S = ⎛

0,24

−0,04 ⎞

⎟,

а корреляционная –

⎛

⎜

0,24

⎝−0,04

−0,04

1,35 ⎠

⎞

⎟

⎜0,49⋅0,49

0,49⋅1,16 ⎟ ⎛ 1

−0,07⎞

R = ⎜

⎟ = ⎜ ⎟ .

⎜ − 0,04

1,35

⎟ ⎝− 0,07 1 ⎠

⎝ 0,49⋅1,16

1,16⋅1,16 ⎠

Теоретические вопросы и задания

1. Что называется дискретной (непрерывной) многомерной случайной величиной?

2. Дайте определение функции распределения многомерной случайной ве-

личины.

3. Сформулируйте определение плотности распределения двумерной непре-

рывной случайной величины.

4. Что называется условным распределением случайной величины?

5. Какие характеристики используются для оценки связи между двумя случайными величинами? Приведите примеры.

6. Какие две случайные величины называются независимыми? некоррелиро-

ванными? Какая связь между этими понятиями?

7. Что называется ковариационной (корреляционной) матрицей многомер-

ной случайной величины?

1. Пусть

( X ,Y )

Задачи и упражнения

– двумерная случайная величина задана законом

распределения:

Y X	-1
	0,04	0,07	0,2	0,1
	0,05	0,1	0,05	0,1
	0,03	0,05	0,06	0,15

а) Найдите законы распределения одномерных случайных величин X и Y ,

их математические ожидания и дисперсии. б) Найдите условные законы

распределения случайной величины X при условии Y = 0

и случайной ве-

личины Y при условии

X =1. в) Определите ковариационную и корреля-

ционную матрицы двумерной величины

( X ,Y ) . г) Вычислите

p( X

<Y ) .

2. Найдите плотность вероятности непрерывной двумерной случайной вели-

чины, заданной функцией распределения:

⎧1 − 2− x −2− y +2− x− y

F ( x, y) = ⎨

⎩0

при x ≥ 0, y ≥ 0,

при x < 0 или y < 0.

3. Имеются две случайные величины X и Y , связанные соотношением

Y = 2 −3X . Известно, что

M ( X ) = −1,

D( X ) = 4 . Найдите:

а) математическое ожидание и дисперсию случайной величины Y ;

б) ковариацию и коэффициент корреляции случайных величин X и Y .

4. Трёхмерная случайная величина принимает значения:

(−1, 0, 0) ,

(−1, 1, 1) ,

(0, 0, 1) ,

(1, 0, 1) ,

(1, 1, −1) . Считая все значения равновероятными, найдите

ковариационную и корреляционную матрицы этой трёхмерной случайной величины, а также её обобщённую дисперсию.

Домашнее задание

1. Двумерная случайная величина определяется следующим образом. Если при подбрасывании игральной кости выпадает четное число очков, то

X =1, в противном случае

X = 0 ;

Y =1, когда число очков кратно трём, в

противном случае

Y = 0 . Найдите: а) законы распределения двумерной

случайной величины

( X , Y )

и ее одномерных компонент; б) условные за-

коны распределения X и Y ; в) коэффициент корреляции

ρ( X , Y ) .

2. Найдите плотность вероятности непрерывной двумерной случайной вели-

чины, заданной функцией распределения:

⎧(1 −e−4 x )(1 −e−2 y )

F ( x, y) = ⎨

⎩0

при x ≥ 0, y ≥ 0,

при x < 0 или y < 0.

3. Имеются две случайные величины X и Y , связанные соотношением

Y = 2X −1. Известно, что

M ( X ) = 2 ,

D( X ) = 4 . Найдите:

а) математическое ожидание и дисперсию случайной величины Y ;

б) ковариацию и коэффициент корреляции случайных величин X и Y .

Занятие 8. Случайные процессы. Контрольная работа

Случайные процессы позволяют изучать случайные явления в динамике их развития.

Определение 8.1. Случайным процессом (функцией)

X (t )

называет-

ся процесс, значение которого при любом значении аргумента t является случайной величиной – сечением случайного процесса.

Определение 8.2. Математическим ожиданием случайного про-

Цесса

X (t )

называется функция

a(t ) , которая при любом значении t равна

математическому ожиданию соответствующего сечения случайного про-

цесса

X (t ) .

Определение 8.3. Дисперсией случайного процесса

X (t )

называется

функция

D(t ) , которая при любом значении t равна дисперсии соответст-

вующего сечения случайного процесса

X (t ) .

Определение 8.4. Средним квадратическим отклонением

σ(t )

Слу-

Чайного процесса

X (t )

называется функция σ(t ) =

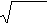D(t ) .

Определение 8.5. Корреляционной функцией случайного процесса

X (t )

называется функция

K (t1 , t2 )

двух переменных t1

и t2 , которая при ка-

ждой паре переменных t1

и t2

равна ковариации соответствующих сечений

X (t1 ) и

X (t2 )

случайного процесса:

K (t1 , t2 ) = M [(X (t1 ) − a(t1 ))⋅(X (t2 ) − a(t2) )].

Замечание. Математическое ожидание случайного процесса характе-

ризует среднюю траекторию всех возможных его реализаций, дисперсия или среднее квадратическое отклонение – разброс реализаций относительно сред-

ней траектории, корреляционная функция – степень тесноты линейной зависимости между двумя сечениями и разброс этих сечений относительно

математического ожидания процесса.

Определение 8.6. Случайный процесс, протекающий в некоторой

системе S с возможными состояниями

S1 ,

S 2 ,…, называется марковским,

если для любого момента времени t0

вероятностные характеристики про-

цесса в будущем ( t > t0 ) зависят только от его состояния в данный момент

t0 и не зависят от того, когда и как система пришла в это состояние.

Определение 8.7. Цепью Маркова называется марковский случайный

процесс, имеющий конечное или счётное число возможных состояний, при- чём переход из одного состояния в другое происходит мгновенно и в опреде- ленные моменты времени.

Пусть цепь Маркова имеет ровно m различных состояний и

pij

– веро-

ятности перехода системы из i -го состояния в j -е. Тогда её полностью мож-

но охарактеризовать матрицей перехода

⎛ p11

⎜

⎜ p21

p12

p22

...

...

p1m ⎞

⎟

p2m ⎟

P = ⎜

⎜

...

...

...

... ⎟ .

⎟

⎝ pm1

pm 2

...

pmm ⎠

Вероятность

pij (n)

перехода системы из i -го состояния в j -е за n ша-

гов равна элементу i -й строки j -го столбца матрицы P n

матрицы P ).

( n -й степени

Пример 8.1. Семьи некоторого региона можно разделить на три груп- пы: 1) не имеющие автомобиля и не собирающиеся его покупать; 2) не имею- щие автомобиля, но намеревающиеся его приобрести; 3) имеющие автомо- биль. Статистическое обследование показало, что матрица перехода в один год имеет вид:

⎛ 0,8

⎜

0,1

0,1⎞

⎟

P = ⎜ 0

⎜

0,7

0,3⎟.

⎟

⎝ 0 0 1 ⎠

Найдите вероятность того, что: а) семья, не имевшая автомобиля и не соби-

равшаяся его покупать, будет находиться в такой же ситуации через два года;

б) семья, не имевшая автомобиля, но намеривавшаяся его приобрести, будет иметь автомобиль через два года.

Решение. Найдем матрицы

P 2 :

⎛0,8

⎜

0,1

0,1⎞

⎟

⎛0,8

⎜

0,1

0,1⎞

⎟

⎟

⎛0,64

⎝

⎜

0,15

0,21⎞

⎟

⎟

P 2 =⎜ 0

0,7

0,3⎟⋅⎜ 0

0,7

0,3⎟= ⎜ 0

0,49

0,51⎟.

⎜ ⎟ ⎜

⎝ ⎠ ⎝

0 1 ⎠ ⎜

0 1 ⎠

Таким образом, искомые вероятности

p11 (2) = 0,64 ,

p23 (2) = 0,51.

Теоретические вопросы и задания

1. Что называется случайным процессом?

2. Дайте определения основным характеристикам случайного процесса.

3. Какой случайный процесс называется марковским? цепью Маркова?

Задачи и упражнения

1. Случайный процесс определяется формулой

X (t ) = X ⋅ e−t

( t > 0 ), где X –

случайная величина, распределенная по нормальному закону с параметра-

ми a и

σ 2 . Найдите математическое ожидание, дисперсию и корреляци-

онную функцию случайного процесса.

2. В моменты времени

t1 ,

t2 , t3

производится аудиторская проверка предпри-

ятия. Возможные заключения:

S1 – нет замечаний,

S2 – имеются несущест-

венные замечания, S3

– имеются существенные замечания,

S4 – по резуль-

татам проверки предприятие прекращает деятельность. Матрица перехода имеет вид:

0,2 0,5 0,5

⎛ 0,2

⎜

⎜

P = ⎜

⎜

0,5

0,2

0,1 ⎞

⎟

0,3⎟

0,5⎟.

⎟

⎝ 1 ⎠

В начальный момент времени предприятие не имеет замечаний. Опреде-

лите вероятность состояний предприятия после трёх проверок.

Домашнее задание

1. Случайный процесс определяется формулой

X (t ) = X ⋅cos 2t , где X – слу-

чайная величина, причем

M ( X ) = 5 ,

D( X ) = 6 . Найдите математическое

ожидание, дисперсию и корреляционную функцию случайного процесса.

2. По результатам года фирма может быть признана: 1) существенно увеличившей товарооборот; 2) существенно уменьшившей товарооборот;

3) не изменившей существенно товарооборот. Опыт показывает, что

матрица перехода из одного состояния в другое за один год имеет вид:

⎛ 0,4

⎜

⎜

P = ⎜0,2

⎝0,3

0,1

0,4

0,3

0,5⎞

⎟

⎠

0,4⎟.

0,4⎟

Найдите вероятность того, что фирма, у которой в этом году товарооборот не изменился, существенно его увеличит через три года.

Образец контрольной работы

1. Трое рабочих изготавливают однотипные изделия. Первый рабочий изго- товил 40 изделий, второй – 35, третий – 25. Вероятность брака у первого рабочего 0,03, у второго – 0,02, у третьего – 0,01. Взятое наугад изделие оказалось бракованным. Определите вероятность того, что это изделие сделал второй рабочий.

2. Магазин заказал 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка разобьётся, равна 0,003. Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение числа разби- тых бутылок.

3. Случайная величина X задана плотностью

p(x) = 2cos2x

в интервале

(0;π /4);

вне этого интервала

p(x) = 0. Найдите математическое ожидание

M(X ).

4. Двумерная случайная величина определяется следующим образом. Если при подбрасывании игральной кости выпадает четное число очков, то

X =1, в противном случае

X = 0 ;

Y =1 , когда число очков кратно трём, в

противном случае Y = 0 . Найдите коэффициент корреляции

ρ( X , Y ) .

Занятие 9. Статистические методы обработки экспериментальных данных. Оценивание и проверка статистических гипотез

Пусть требуется изучить некоторую совокупность однородных объектов относительно некоторого количественного признака (показателя) X .

Определение 9.1. Генеральной совокупностью называется множе-

ство всех подлежащих изучению объектов.

Понятие генеральной совокупности аналогично понятию случайной ве- личины, поэтому можно говорить о виде распределения генеральной сово- купности.

Определение 9.2. Выборочной совокупностью (выборкой) называ- ется множество случайно отобранных объектов из генеральной совокупно- сти, а количество объектов в выборке – объёмом выборки.

Определение 9.3. Наблюдаемые значения признака в выборке назы-

ваются вариантами.

Определение 9.4. Вариационным рядом (статистическим распреде- лением выборки) называется ряд вариантов, расположенных в порядке воз- растания с соответствующими им частотами (или относительными час- тотами).

Определение 9.5. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным(интервальным), если варианты могут отличаться друг от друга сколь угодно мало.

Определение 9.6. Эмпирической функцией распределения называется

функция

F * ( x) , которая для каждого действительного числа x равна отно-

сительной частоте того, что признак примет значение, меньшее x :

X < x .

Все свойства функции распределения случайной величины справедливы и для эмпирической функции распределения.

Для графического представления вариационных рядов наиболее часто используют полигон и гистограмму.

Определение 9.7. Полигоном частот дискретного вариационного

ряда называется ломаная, соединяющая точки

( x1 , n1 ) , …,

( xk , nk ) , где

xi –

варианты, а ni

– соответствующие им частоты.

Определение 9.8. Гистограммой относительных частот интервального вариационного ряда называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы

k

длины h значений признака, а высоты равны величинам

ni , где

n = ∑ni –

объём выборки.

nh i=1