Понятие о центральной предельной теореме и законе больших чисел

Определение 6.1. Непрерывная случайная величина X имеет нор-

мальный закон распределения с параметрами aи σ, если её плотность ве-

роятности имеет вид:

p( x) =

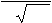σ

( x−a)2

1 e− 2σ2 .

2π

Свойства случайных величин, распределенных по нормальному закону

1. Математическое ожидание

M( X)

случайной величины X, распределен-

ной по нормальному закону, равно параметру a , а дисперсия

раметру σ2 .

D( X )

– па-

2. Вероятность попадания случайной величины Xв промежуток [α; β] равна

P(α≤ X

≤β) =Φ⎛= β−a⎞−Φ⎛α=

− a⎞.

σ

⎜ ⎟ ⎜ ⎟

⎝ ⎠ ⎝ σ ⎠

3. Вероятность отклонения случайной величины X от её математического

ожидания не более чем на ε> 0

равна

⎛ ε⎞

P(| X

− M( X) | ≤ ε)= 2Φ⎜ ⎟ .

⎝σ⎠

Важность случайных величин, имеющих нормальное распределение,

обусловлена одной из центральных предельных теорем – теоремой Ляпуно- ва7, суть которой заключается в следующем: если случайная величина X представляет собой сумму достаточно большого количества попарно незави- симых случайных величин, влияние каждой из которых на всю сумму ни- чтожно мало, то есть основания предположить, что X имеет распределение, близкое к нормальному.

7 Александр Михайлович Ляпунов (1857 – 1918) – русский математик.

Под законом больших чисел понимается общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит при некоторых условиях к результату, почти не зависящему от случая. Важно отметить, что закон больших чисел справедлив как для дискретных, так и для непрерывных случайных величин.

К закону больших чисел относятся следующие теоремы.

Теорема 6.1 (неравенство Маркова8). Если случайная величина X

принимает только неотрицательныезначения и имеет математическое

ожидание

M( X) , то для любого положительного числа εверно неравенство

P( X

>ε) ≤ M( X) .

ε

Замечание. Из неравенства Маркова следует

P( X

≤ε) ≥1 − M( X) .

ε

Теорема 6.2 (неравенство Чебышева9). Если случайная величина

Xимеет математическое ожидание

M( X)

и дисперсию

D( X) , то для лю-

бого положительного числа εверно неравенство

P(| X

− M( X) |>ε) ≤ D( X) .

ε2

Замечание. Другая форма неравенства Чебышева:

P(| X− M(X) |≤ε) ≥1− D(X) .

ε2

Из последнего неравенства, в частности, следует правило трёх сигм:

P(| X− M(X) |≤3σ) ≥1−

σ

9σ2

= 8 ≈ 0,889.

Теорема 6.3 (теорема Чебышева). Если попарно независимые слу-

чайные величины

X1 ,

X2 , …,

Xn, … имеют конечные математические

ожидания и их дисперсии равномерно ограничены (не превышают постоян- ного числа С ), то средняя арифметическая этих случайных величин сходит- ся по вероятности к среднему арифметическому их математических ожи-

даний, т.е. для любого положительного числа ε

⎛ 1 n

⎝

i

lim P⎜ ∑ X

1 n

i

− ∑ M( X

) < ε

⎞

⎠

⎟ = 1.

n→∞

⎜ ni=1

ni=1 ⎟

Теорема 6.4 (теорема Бернулли). Частота случайного события в n

повторных независимых испытаниях, в каждом из которых оно может про-

изойти с одной и той же вероятностью p, при неограниченном увеличении

8 Андрей Андреевич Марков (1856 – 1922) – русский математик.

9 Пафнутий Львович Чебышев (1821 – 1894) – русский математик и механик.

числа испытаний n сходится по вероятности к вероятности p , т.е. для

любого положительного числа ε

⎜

limP⎛

m− p

⎞

<ε⎟ =1.

n→∞ ⎝ n ⎠

Пример 6.1. В среднем 10% работоспособного населения некоторого региона – безработные. Оцените с помощью неравенства Чебышева вероят- ность того, что уровень безработицы среди обследованных 10 000 работоспо- собных жителей региона будет в пределах от 9 до 11% (включительно). Опре- делите эту вероятность точно с помощью интегральной теоремы Муавра- Лапласа.

Решение. По условию вероятность того, что наугад выбранный работо-

способный житель региона будет безработным, равна

p= 0,1 . Так как слу-

чайная величина X – число безработных среди обследованных

n=10 000

жителей – распределена по биномиальному закону, то

M( X) = np=1000 ,

D( X) = npq= 900 . Таким образом, вероятность отклонения X от среднего

значения на 1%, т.е. на 100 жителей, может быть оценена с помощью нера-

венства Чебышева:

P(| X− M(X) |≤100) ≥1−

= 0,91.

Уточним теперь эту вероятность с помощью интегральной теоремы

Муавра-Лапласа:

⎞

⎛

P(| X− M(X) |≤100) = 2Φ⎜

⎟ = 2Φ(3,33)= 2⋅0,4996 = 0,9992.

⎝ 900 ⎠

Теоретические вопросы и задания

1. Какая случайная величина называется нормальной? Приведите примеры таких величин.

2. Сформулируйте свойства случайных величин, имеющих нормальное рас-

пределение.

3. В чем заключается суть теоремы Ляпунова?

4. Что понимается под законом больших чисел? Какие теоремы, относящие-

ся к закону больших чисел, Вы знаете?

5. Какой вид имеют неравенства Маркова и Чебышева? При каких условиях они применимы?

6. Сформулируйте теоремы Чебышева и Бернулли.

Задачи и упражнения

1. Случайная величина X имеет плотность распределения вероятностей

p(x) =

2 ⎛

exp⎜ −

(x−1)2 ⎞

⎟

⎟ . Найдите: а) математическое ожидание X ;

⎜

18π ⎝

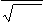
4,5 ⎠

б) дисперсию X ; в) вероятность того, что X примет значение, мень-

шее 0,5; г) вероятность того, что X примет значение, большее 2;

д) вероятность того, что X примет значение из интервала

(1; 2) ;

е) вероятность того, что абсолютная величина отклонения X от матема-

тического ожидания не превысит 3.

2. Завод выпускает детали, стандартная длина которых

a=114

мм. Длина де-

тали – случайная величина, распределенная по нормальному закону со

средним квадратическим отклонением σ=8

мм и математическим ожида-

нием a. Определите: а) вероятность того, что длина наудачу выбранной

детали будет больше α=106

мм и меньше

β=117

мм; б) вероятность от-

клонения длины детали от стандартного размера не более чем на δ= 2

мм;

в) вероятность того, что из трёх выбранных деталей у двух отклонение

длины от стандартного размера будет не более δ= 2

мм.

3. Предположим, что в течение года цена на акции некоторой компании есть

нормально распределенная случайная величина с параметрами

a= 49

у.е. и

σ= 4

у.е. Определите вероятность того, что в случайно выбранный день года

цена за акцию составила: а) более 57 у.е.; б) менее 57 у.е.; в) между 45 и 59 у.е.

4. Автоматически изготовленные детали по длине распределены нормально и расположены в интервале от 29,7 до 30,3 см. Какой длины проектирова- лась деталь и с каким допуском?

5. Суточное потребление электроэнергии исправной печью является случай-

ной величиной, распределенной по нормальному закону со средним значе-

нием 1000 кВт и средним квадратическим отклонением

σ= 35

кВт. Если

суточное потребление превысит 1100 кВт, то по инструкции печь отклю- чают и ремонтируют. а) Найдите вероятность ремонта печи. б) Каким должно быть превышение по инструкции, чтобы вероятность ремонта печи была равна 0,02?

6. Отделение банка обслуживает в среднем 100 клиентов в день. Оцените ве- роятность того, что сегодня в отделении банка будет обслужено: а) не бо- лее 200 клиентов; б) более 150 клиентов.

7. Дневная выручка магазина является нормально распределенной случайной величиной со средним значением 10000 руб. и средним квадратичным от- клонением 2000 руб. Оцените с помощью неравенства Чебышева вероят- ность того, что дневная выручка будет находиться в пределах от 6000 до

14000 руб. Уточните ответ, учитывая, что дневная выручка магазина явля-

ется случайной величиной, распределенной по нормальному закону.

Домашнее задание

1. Ошибка взвешивания – случайная величина, распределенная по нормаль- ному закону с математическим ожиданием, равным нулю, и среднеквадра- тическим отклонением, равным 2 г. Найдите вероятность того, что взве- шивание проведено с ошибкой, не превышающей по модулю 4 г.

2. Средняя масса плодов в одном ящике равна 10 кг. Фактическая масса пло- дов в ящике – случайная величина со средним квадратическим отклонени- ем 0,6 кг. Найдите: а) вероятность того, что фактическая масса отклонится от средней не более чем на 1 кг; б) массу, ниже которой фактическая мас- са не опустится с вероятностью 0,97.

3. Телефонная станция обслуживает

n=100

абонентов. Вероятность того,

что любой абонент позвонит в течение часа, равна р=0,9. а) Найдите сред- нее и дисперсию числа вызовов. б) С помощью неравенства Чебышева оцените вероятность отклонения числа вызовов от среднего не более чем на 5. в) Уточните ответ, воспользовавшись интегральной теоремой Муав- ра-Лапласа.

4. Самый популярный размер мужской обуви – 42. Известно также, что 91% мужчин носят обувь до 44 размера включительно. Считая, что случайная величина – размер обуви – подчиняется нормальному закону распределе- ния, найдите вероятность того, что из четырёх мужчин хотя бы один будет иметь размер обуви, меньший 41.

Занятие 7. Системы случайных величин.