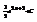В какой точке касательная к графику функции
В какой точке касательная к графику функции
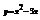 образует с осью
образует с осью  угол 450? (2;−2)
угол 450? (2;−2)
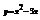 образует с осью
образует с осью 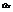 угол 1350?(1;−2)
угол 1350?(1;−2)
Векторы 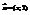 и
и 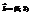 коллинеарны. Найти число х. 4
коллинеарны. Найти число х. 4
Векторы
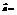 (3; −2) и
(3; −2) и 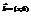 перпендикулярны. Найти х. 4
перпендикулярны. Найти х. 4
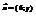 и
и 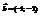 перпендикулярны. Найти y.−3
перпендикулярны. Найти y.−3
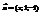 и
и 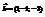 перпендикулярны. Найти х.−2
перпендикулярны. Найти х.−2
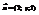 и
и 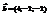 перпендикулярны. Найти y.3
перпендикулярны. Найти y.3
Вычислить интеграл
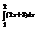 .6
.6
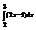 .4
.4
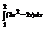 .4
.4
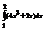 .18
.18
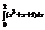 .8
.8
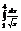 .2
.2
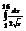 . 3
. 3
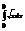 .18
.18
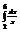 .
. 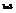
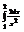 .1
.1
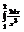 .
. 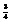
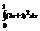 . 7
. 7
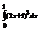 .10
.10
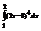 .0,2
.0,2
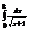 .4
.4
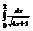 .1
.1
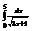 .2
.2
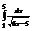 .
. 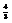
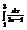 .
. 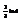
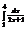 .
. 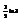
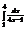 .
. 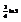
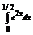 .
. 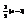
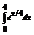 .
. 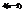
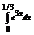 .
. 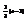
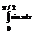 .1
.1
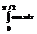 .1
.1
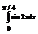 .0,5
.0,5
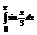 .1,5
.1,5
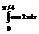 .0,5
.0,5
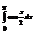 .2
.2
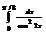 0,5
0,5
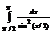 .2
.2
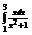 .
. 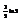
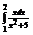 .
. 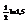
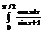 .
. 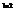
Вычислить площадь фигуры, ограниченной линиями
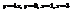 .16
.16
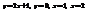 . 4
. 4
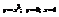 .0,25
.0,25
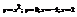 .3
.3
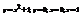 .
. 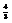
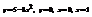 .4
.4
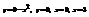 .18
.18
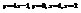 .5
.5
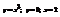 .4
.4
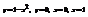 .
. 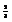
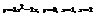 .4
.4
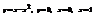 .
. 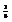
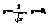
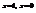 . 4
. 4
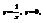
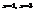 .
. 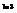
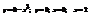 .12
.12
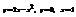 .
. 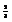
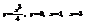 . 5
. 5
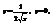
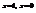 . 2
. 2
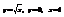 .
. 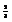
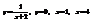 .
. 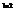
Вычислить ранг матрицы
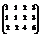 . 1
. 1
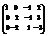 .2
.2
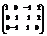 . 3
. 3
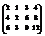 . 1
. 1
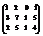 . 2
. 2
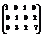 . 3
. 3
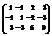 .1
.1
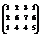 .2
.2
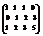 . 3
. 3
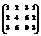 . 1
. 1
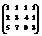 . 2
. 2
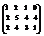 . 3
. 3
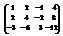 . 1
. 1
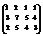 . 2
. 2
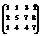 .3
.3
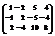 .1
.1
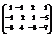 .2
.2
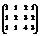 .3
.3
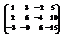 .1
.1
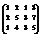 . 2
. 2
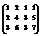 . 3
. 3
Вычислить определитель
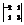 .−7
.−7
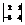 .11
.11
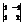 .3
.3
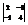 .5
.5
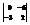 .0
.0
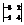 .−10
.−10
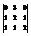 . −3
. −3
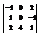 . 4
. 4
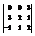 . 15
. 15
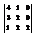 .10
.10
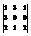 .−15
.−15
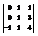 . −2
. −2
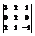 .−10
.−10
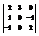 . −3
. −3
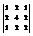 .0
.0
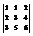 .0
.0
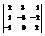 .−15
.−15
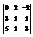 .−4
.−4
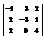 . 6
. 6
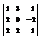 .−10
.−10
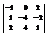 .20
.20
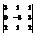 . −15
. −15
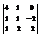 . 20
. 20
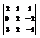 . −8
. −8
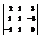 . 15
. 15
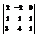 .−10
.−10
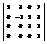 .–15
.–15
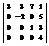 .–24
.–24
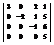 .30
.30
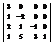 .6
.6
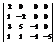 .–20
.–20
График функции 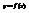 будет выпуклым
будет выпуклым
вверх на интервале 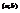 , если для всех значений
, если для всех значений 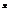 из этого интервала выполняется условие:
из этого интервала выполняется условие: 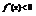
вниз на интервале 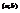 , если для всех значений
, если для всех значений 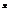 из этого интервала выполняется условие:
из этого интервала выполняется условие: 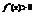
Дана прямая
x−5y+2=0. Какие из точек M(3; 1), N(1; 5), P(1; 3), Q(8; 2) лежат на этой прямой? M, Q
2x+y−3=0. Какие из точек M(1; 1), N(1; −1), P(2; −1),Q(1; 2) лежат на этой прямой? M, P
Дана система уравнений
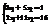 . Вычислить
. Вычислить 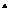 .23
.23
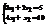 . Вычислить
. Вычислить 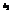 .−15
.−15
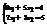 . Вычислить
. Вычислить 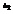 .33
.33
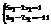 . Вычислить
. Вычислить 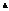 . –29
. –29
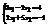 . Вычислить
. Вычислить 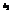 . 18
. 18
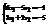 . Вычислить
. Вычислить 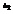 .–27
.–27
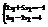 . Найти
. Найти 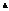 .–19
.–19
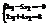 . Найти
. Найти 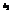 .4
.4
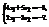 . Найти
. Найти 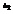 .–22
.–22
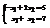 . Найти x1. 3
. Найти x1. 3
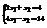 . Найти x2.−2
. Найти x2.−2
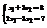 . Найти
. Найти 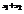 .6
.6
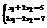 . Найти
. Найти 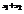 .4
.4
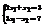 . Найти
. Найти 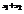 . 1
. 1
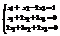 . Найти
. Найти 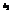 . −5
. −5
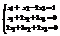 . Найти
. Найти 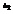 .4
.4
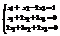 . Найти
. Найти 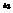 .−1
.−1
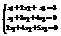 . Найти
. Найти 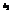 .−3
.−3
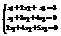 . Найти
. Найти 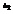 .9
.9
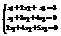 . Найти
. Найти 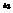 .-6
.-6
Дана функция
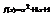 . Вычислить
. Вычислить 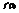 . 5
. 5
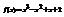 . Вычислить
. Вычислить 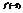 .6
.6
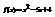 . Вычислить
. Вычислить 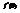 .−5
.−5
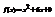 . Вычислить
. Вычислить 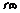 .10
.10
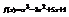 . Вычислить
. Вычислить 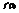 .2
.2
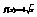 . Вычислить
. Вычислить 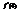 . 1
. 1
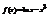 . Вычислить
. Вычислить 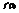 .−2
.−2
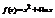 . Вычислить
. Вычислить 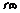 . 6
. 6
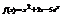 . Вычислить
. Вычислить 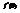 .−3
.−3
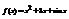 . Вычислить
. Вычислить 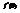 .4
.4
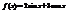 . Вычислить
. Вычислить 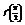 . −3
. −3
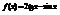 . Вычислить
. Вычислить 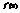 .3
.3
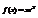 . Вычислить
. Вычислить 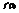 .
. 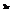
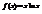 . Вычислить
. Вычислить 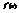 .2
.2
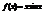 . Вычислить
. Вычислить 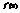 .
. 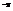
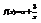 . Вычислить
. Вычислить 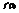 . –2
. –2
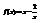 . Вычислить
. Вычислить 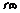 . 1,5
. 1,5
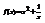 . Вычислить
. Вычислить 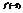 . –3
. –3
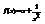 . Вычислить
. Вычислить 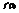 . –1
. –1
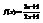 . Вычислить
. Вычислить 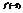 . 1
. 1
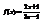 . Вычислить
. Вычислить 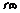 . –0,2
. –0,2
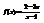 . Вычислить
. Вычислить 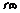 . 1
. 1
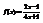 . Вычислить
. Вычислить 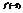 .
. 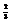
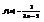 . Вычислить
. Вычислить 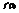 . −3
. −3
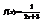 . Вычислить
. Вычислить 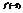 . −2
. −2
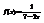 . Вычислить
. Вычислить 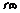 .
. 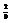
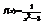 . Вычислить
. Вычислить 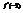 . 4
. 4
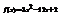 . Найти
. Найти 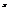 , если
, если 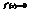 . 2
. 2
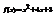 . Найти
. Найти 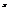 , если
, если 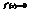 . −2
. −2
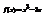 . Найти
. Найти 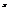 , если
, если 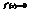 . −1; 1
. −1; 1
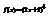 . Вычислить
. Вычислить 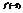 .−8
.−8
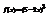 . Вычислить
. Вычислить 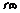 .−6
.−6
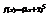 . Вычислить
. Вычислить 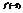 . 15
. 15
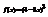 . Вычислить
. Вычислить 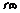 . −36
. −36
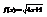 . Вычислить
. Вычислить 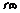 .
. 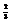
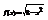 . Вычислить
. Вычислить 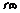 . −1
. −1
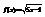 . Вычислить
. Вычислить 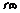 .
. 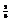
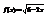 . Вычислить
. Вычислить 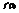 .–0,5
.–0,5
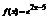 . Вычислить
. Вычислить 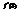 .2е
.2е
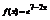 . Вычислить
. Вычислить 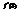 .−2е
.−2е
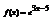 . Вычислить
. Вычислить 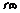 .
. 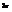
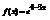 . Вычислить
. Вычислить 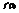 . –3е
. –3е
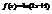 . Вычислить
. Вычислить 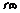 .0,4
.0,4
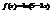 . Вычислить
. Вычислить 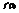 .–1,5
.–1,5
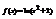 . Вычислить
. Вычислить 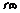 .
. 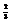
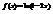 . Вычислить
. Вычислить 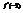 . –0,4
. –0,4
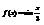 . Вычислить
. Вычислить 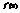 .
. 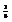
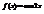 . Вычислить
. Вычислить 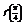 . −2
. −2
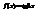 . Вычислить
. Вычислить 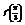 .3
.3
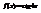 . Вычислить
. Вычислить 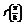 .−4
.−4
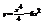 . Найти
. Найти 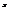 , если
, если 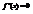 .−2; 2
.−2; 2
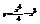 . Найти
. Найти 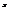 , если
, если 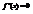 .0; 2
.0; 2
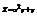 . Найти
. Найти 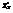 .
. 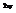
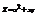 . Найти
. Найти 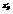 .
. 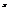
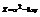 . Вычислить
. Вычислить 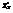 в точке (1; 1).−1
в точке (1; 1).−1
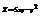 . Вычислить
. Вычислить 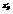 в точке (1;−2).9
в точке (1;−2).9
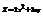 . Вычислить
. Вычислить 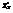 в точке (−1; 1).−1
в точке (−1; 1).−1
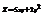 . Вычислить
. Вычислить 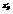 в точке (−1; 2).3
в точке (−1; 2).3
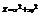 . Вычислить
. Вычислить 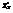 в точке (1; −2). 6
в точке (1; −2). 6
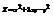 . Вычислить
. Вычислить 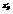 в точке (2; 1).4
в точке (2; 1).4
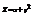 . Найти
. Найти 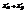 в точке (1; 1).3
в точке (1; 1).3
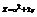 . Найти
. Найти 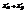 в точке (2; 1).6
в точке (2; 1).6
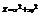 . Найти
. Найти 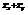 в точке (−1; −2). 6
в точке (−1; −2). 6
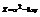 . Найти
. Найти 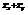 в точке (1; −1). 2
в точке (1; −1). 2
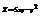 . Найти
. Найти 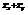 в точке (1; −2). –1
в точке (1; −2). –1
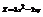 . Найти
. Найти 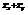 в точке (1; −1). 6
в точке (1; −1). 6
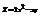 . Найти
. Найти 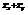 в точке (−1; 2). –5
в точке (−1; 2). –5
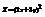 . Вычислить
. Вычислить 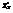 в точке (1; −1). −4
в точке (1; −1). −4
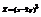 . Вычислить
. Вычислить 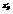 в точке (3; 1). −6
в точке (3; 1). −6
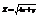 . Вычислить
. Вычислить 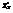 в точке (2; 1).
в точке (2; 1). 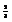
 . Вычислить
. Вычислить 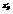 в точке (5; 1).
в точке (5; 1). 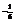
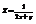 . Вычислить
. Вычислить 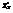 в точке (1; −1).−2
в точке (1; −1).−2
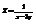 . Вычислить
. Вычислить 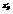 в точке (6; 1).
в точке (6; 1). 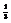
 . Вычислить
. Вычислить 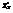 в точке (0; 0).3
в точке (0; 0).3
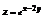 . Вычислить
. Вычислить 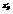 в точке (0; 0).−2
в точке (0; 0).−2
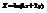 . Вычислить
. Вычислить 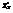 в точке (1; 1).
в точке (1; 1). 
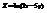 . Вычислить
. Вычислить 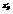 в точке (3; 1).−5
в точке (3; 1).−5
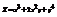 . Найти
. Найти 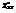 .
. 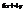
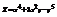 . Найти
. Найти 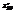 .
. 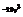
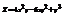 . Найти
. Найти 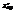 .
. 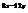
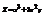 . Найти
. Найти 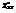 в точке (1; 2).18
в точке (1; 2).18
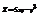 . Найти
. Найти 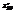 в точке (2; −1) .6
в точке (2; −1) .6
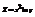 . Найти
. Найти 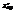 в точке (−1;2) .−1
в точке (−1;2) .−1
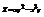 . Найти
. Найти 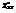 в точке (1; −2).12
в точке (1; −2).12
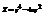 . Найти
. Найти 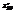 в точке (2; 1) .−4
в точке (2; 1) .−4
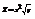 . Найти
. Найти 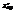 в точке (6; 4).3
в точке (6; 4).3
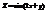 . Найти
. Найти 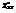 в точке
в точке 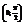 .−4
.−4
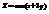 . Найти
. Найти 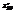 в точке (π; 0) .9
в точке (π; 0) .9
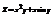 . Найти
. Найти 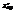 в точке (1; 0). 3
в точке (1; 0). 3
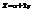 . Найти
. Найти 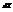 .
. 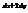
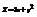 . Найти
. Найти 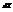 .
. 
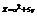 . Найти
. Найти 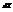 .
. 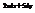
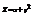 . Найти
. Найти 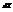 .
. 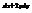
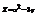 . Найти
. Найти 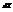 .
. 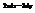
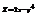 . Найти
. Найти 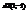 .
. 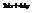
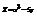 . Найти
. Найти 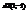 .
. 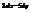
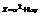 . Найти
. Найти 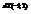 .
. 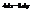
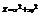 . Найти
. Найти 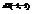 .
. 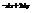
Даны векторы
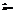 (−1; 2) и
(−1; 2) и 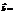 (2; −3) . Найти вектор
(2; −3) . Найти вектор 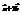 .(3; −4)
.(3; −4)
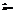 (4; 5) и
(4; 5) и 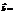 (2; 3). Найти вектор
(2; 3). Найти вектор 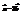 .(−2; −4)
.(−2; −4)
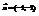 ,
, 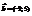 . Найти вектор
. Найти вектор 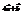 .(−6; −3)
.(−6; −3)
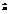 (3; −2) и
(3; −2) и 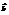 (1; 1). Найти вектор
(1; 1). Найти вектор 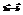 .(5; −5)
.(5; −5)
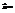 (−1; 1) и
(−1; 1) и 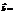 (−3; 2). Найти вектор
(−3; 2). Найти вектор 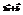 .(−5; 4)
.(−5; 4)
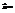 (2; 2; −1) и
(2; 2; −1) и 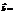 (0; 4; 1). Найти вектор
(0; 4; 1). Найти вектор 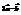 .(6;2; −4)
.(6;2; −4)
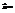 (−1; 1; 1) и
(−1; 1; 1) и 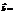 (0; 2; 1). Найти вектор
(0; 2; 1). Найти вектор 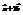 . (−1;5;3)
. (−1;5;3)
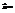 (4; −1; 2) и
(4; −1; 2) и 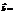 (2; 1; −1). Найти вектор
(2; 1; −1). Найти вектор 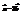 . (−2;−4;5)
. (−2;−4;5)
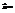 (3; 4; 1) и
(3; 4; 1) и 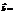 (−1; −2; −1). Найти вектор
(−1; −2; −1). Найти вектор 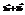 .(3; 2; −1)
.(3; 2; −1)
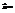 (3; 0; 2) и
(3; 0; 2) и 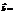 (1; −2; −1). Найти вектор
(1; −2; −1). Найти вектор 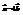 .(−1; 8; 6)
.(−1; 8; 6)
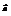 =(8; −4) и
=(8; −4) и 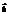 = (−4; 1). Найти длину вектора
= (−4; 1). Найти длину вектора 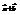 .5
.5
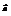 =(8; −4) и
=(8; −4) и 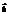 = (−4; 1). Найти длину вектора
= (−4; 1). Найти длину вектора 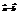 .13
.13
Две плоскости 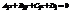 и
и 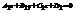
параллельны, если выполняется условие: 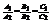
перпендикулярны, если выполняется условие: 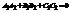
Достаточным условием
минимума дифференцируемой функции 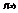 в критической точке
в критической точке 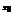 является: изменение знака производной с минуса на плюс в точке
является: изменение знака производной с минуса на плюс в точке 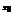
максимума дифференцируемой функции 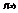 в критической точке
в критической точке 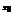 является: изменение знака производной с плюса на минус в точке
является: изменение знака производной с плюса на минус в точке 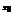
Если скалярное произведение векторов 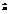 и
и 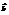 равно
равно
0, то угол между этими векторами: 900
2, то угол между этими векторами: острый
−5, то угол между этими векторами тупой
Если угол между векторами 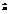 и
и 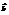 равен
равен
900, то скалярное произведение этих векторов равно: 0
00, то скалярное произведение этих векторов равно: 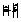
1800, то скалярное произведение этих векторов равно: 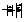
Имеет ли функция 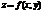 экстремум в критической точке, если в этой точке
экстремум в критической точке, если в этой точке
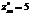 ,
, 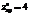 ,
, 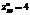 ?минимум
?минимум
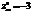 ,
, 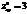 ,
, 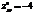 ?максимум
?максимум
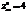 ,
, 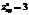 ,
, 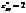 ?нет экстремума
?нет экстремума
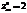 ,
, 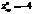 ,
, 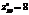 ? экстремум может быть, а может и не быть
? экстремум может быть, а может и не быть
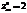 ,
, 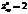 ,
, 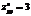 ? минимум
? минимум
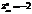 ,
, 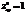 ,
, 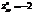 ?максимум
?максимум
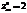 ,
, 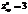 ,
, 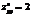 ?нет экстремума
?нет экстремума
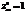 ,
, 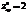 ,
, 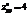 ? экстремум может быть, а может и не быть
? экстремум может быть, а может и не быть
Найти дифференциал функции
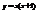 .
. 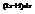
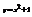 .
. 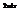
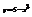 .
. 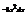
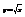 .
. 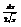
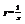 .
. 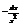
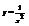 .
. 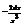
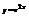 .
. 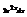
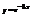 .
. 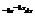
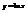 .
. 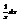
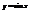 .
. 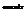
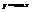 .
. 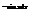
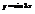 .
. 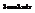
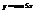 .
. 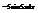
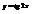 .
. 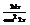
Найти точку перегиба кривой
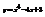 .нет точек перегиба
.нет точек перегиба
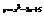 .(0; 5)
.(0; 5)
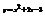 .нет точек перегиба
.нет точек перегиба
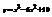 .(2; −6)
.(2; −6)
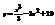 . (3; 2)
. (3; 2)
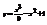 .(3; −5)
.(3; −5)
Найти градиент функции
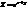 в точке (0;0).(1; −3)
в точке (0;0).(1; −3)
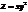 в точке (1; 1).(1; 2)
в точке (1; 1).(1; 2)
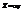 в точке (3;4). (4; 3)
в точке (3;4). (4; 3)
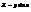 в точке (
в точке ( 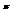 ; 1).(−1; 0)
; 1).(−1; 0)
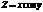 в точке
в точке 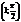 .(0; −1)
.(0; −1)
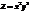 в точке (1; −1).(−2; 3)
в точке (1; −1).(−2; 3)
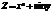 в точке (1;
в точке (1;  ).(4; −1)
).(4; −1)
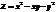 в точке (1;1).(1; −3)
в точке (1;1).(1; −3)
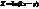 в точке (2; 3).(2; −1)
в точке (2; 3).(2; −1)
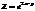 в точке (0; 0).(2; −1)
в точке (0; 0).(2; −1)
Найти длину вектора
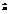 =(1;−1;−1).
=(1;−1;−1). 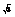
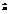 =(2;−1;2). 3
=(2;−1;2). 3
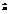 =(6;−2;−3). 7
=(6;−2;−3). 7
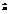 =(8; −4; −1).9
=(8; −4; −1).9
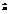 =(4; 2;−4).6
=(4; 2;−4).6
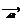 , если A(4; 0) и B(1; 4).5
, если A(4; 0) и B(1; 4).5
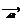 , если A(1; 2) и B(−3;−1). 5
, если A(1; 2) и B(−3;−1). 5
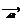 , если A(−2; 1) и B(6;−5).10
, если A(−2; 1) и B(6;−5).10
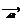 , если A(−2; 1; 3) и B(−1; 3; 1).3
, если A(−2; 1; 3) и B(−1; 3; 1).3
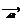 , если A(−2; −1; 2) и B(6; −5; 3). 9
, если A(−2; −1; 2) и B(6; −5; 3). 9
Найти интеграл
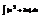 .
. 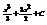
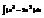 .
. 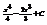
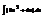 .
. 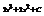
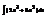 .
. 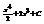
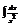 .
. 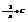
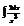 .
. 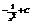
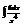 .
. 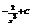
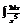 .
. 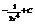
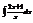 .
. 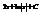
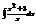 .
. 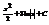
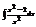 .
. 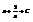
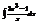 .
. 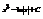
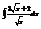 .
. 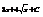
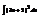 .
. 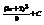
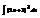 .
. 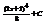
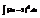
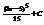
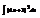 .
. 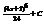
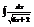 .
. 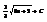
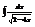 .
. 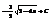
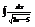 .
. 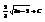
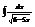 .
. 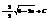
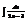 .
. 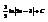
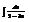 .
. 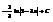
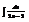 .
. 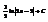
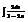 .
. 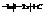
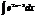 .
. 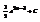
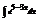 .
. 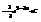
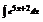 .
.