Понятие о системном подходе и системном анализе

Понятие о системном подходе и системном анализе

Системные исследования

1.1. Раздробление наук

Современной особенностью развития науки является возрастающая дифференциация фундаментальных и прикладных направлений. В науке возникла очень сложная иерархия специализированных дисциплин: математика, физика, биология, психология и многие другие. На место древнего ученого, такого как Аристотель, пришли поколения ученых, обладающих все большей глубиной знаний и все большей узостью интересов и компетенций. По мнению известного американского ученого системолога Дж. Клира основной причиной, породившей тенденцию к разделению науки на узкие специальности, является ограниченная возможность человеческого разума. Поскольку объем знаний стал больше того, который человек в состоянии воспринять, всякое увеличение знаний необходимо приводит к тому, что человек может охватить все меньшую ее часть. Чем глубже это знание, тем уже специализированно оно должно быть. Углубление специализации присуще не только естественным наукам. В других областях человеческой деятельности, например, технике, медицине, искусстве наблюдается та же тенденция.

1.2.Появление системных исследований

Одной из главной особенностей науки второй половины XXв. является появление ряда родственных научных направлений, обобщающих и интегрирующих специализированные знания, ведущих работу на общем поле исследований, которое получило название «Системные исследования». Это поле схематично представлено на рис.1.1.

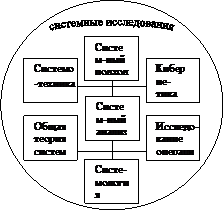Рис.1.1 Системные исследования

Все эти системные дисциплины взаимосвязаны и тесно переплетаются, пересекаются, имея много общего, но в то же время и много специфических особенностей.

Системный подход

В литературе по системной методологии термин «системный подход» трактуется как одна из форм методологического знания, непосредственно связанная с исследованием и проектированием объекта как системы, как методологическое основание системного анализа. При этом признаками системного подхода считаются следующие особенности исследований и разработок:

1. Рассмотрение изучаемого или разрабатываемого объекта как целого (системы);

2. Представление его как множество членений с установлением взаимосвязи между ними;

3. Проведение анализа отношений и связи элементов системы между собой, а также данной системы с другими системами;

4. Установление структуры исследуемой системы;

5. Изучение ее иерархического строения;

6. Определение цели системы;

7. Выделение и описание информационных потоков в системе;

8. Применение информационных технологий.

Системный подход – направление методологии научного познания, в основе которого лежит рассмотрение объектов как систем.

Системный анализ

Термин «системный анализ» в общей системологии понимается как теоретическая дисциплина, развивающая методы проектирования сложных технических и экономических систем. Системный анализ считается развитием теории исследования операции, которое включает в себя последнюю со всем арсеналом средств, созданных в ее рамках.

Системный анализ – совокупность методологических средств, используемых для подготовки и обоснования решений по сложным проблемам научного и технического характера.

Определение системы

Основные понятия, входящие в определение системы

2.1.Элемент

Под элементом принято понимать простейшую неделимую часть системы. Однако ответ на вопрос «Что является такой частью?» может быть неоднозначным. Поэтому примем следующее определение:

Элемент – предел членения системы с точки зрения аспекта рассмотрения системы, решения конкретной задачи, поставленной цели.

Систему можно расчленить на элементы различными способами в зависимости от формулировки задачи и цели. При многоуровневом членении сложной системы используют другой термин – «подсистема». Названием «подсистема» подчеркивается, что такая часть должна обладать свойствами системы (целостность, наличие цели). Этим подсистема отличается от группы элементов, для которых не определяется цель, не выполняется свойство целостности

2.2.Отношения (связь)

Связь – ограничение степени свободы элементов. Связи можно характеризовать направлением, силой, характером, местом приложения и др. Особенно важной характеристикой отношений и связей является их сила или мощность. Система существует как некоторое целостное образование тогда и только тогда, когда мощность (сила) существенных связей между элементами больше мощности связи этих элементов с окружающей средой.

2.3.Цель

Понятие «цель» и связанные с ним понятия «целесообразности», «целенаправленности» лежит в основе развития системы. В зависимости от стадии познания объекта (этапа системного анализа) в понятие «цель» вкладываются различные оттенки от идеальных, философских (цель – выражение активности сознания) до конечных результатов процесса, формируемых в терминах конечного продукта деятельности. В энциклопедии дается такое определение.

Цель – это заранее мыслимый результат сознательной деятельности человека.

2.4.Целостность

Если каждая часть системы так соотносится с другой каждой ее частью, что изменение в некоторой части вызывает изменение во всех других частях и во всей системе в целом, то говорят, что система ведет себя как целостность или как некоторое связанное образование. Объект называется целостным в тех случаях, когда он рассматривается как состоящий из частей, которые не существуют и не могут быть зафиксированы по отдельности вне их соотношения друг с другом.

Классификация системы

Системы разделяют на классы по различным признакам и в зависимости от решаемой задачи можно выбирать разные принципы классификации:

1. По виду отображаемого объекта: технические, биологические, экономические, космические и т.д.;

2. По виду научного направления: математические, физические, химические, информационные;

3. По виду обмена со средой: открытые и закрытые;

4. По сложности: простые (малые) и сложные (большие).

Понятие о системе качества

Определение этого понятия приведено в международном стандарте ИСО 9000:2000. На рис.2.2 показана схема формирования этого понятия.

Рис.2.2 Схема формирования понятия системы менеджмента качества

Понятие о структуре

В литературе встречается большое число различных определений структуры. Рассмотрим наиболее типичные из них:

а. «структура есть форма представления некоторого объекта в виде составных частей»;

б. «структура – это множество всех возможных отношений между подсистемами и элементами внутри системы»;

в. «структура – это то, что остается неизменным в системе при изменении ее состояния и поведения».

В совокупности данные определения достаточно хорошо отражают то главное, что присутствует в любой структуре. Мы будем далее использовать следующее определение.

«Структура – это то, что отражает взаимосвязи, взаиморасположения составных частей системы, ее устройство (строение, конфигурацию)»

Следует учитывать, что для одной и той же системы можно построить различные структуры, т.к. в зависимости от целей изучения исследователей могут интересовать различные инвариантные (неизменные) во времени свойства системы. Рассмотрим теперь основные методы описания структур системы.

Структурные схемы

Если изобразить систему как совокупность блоков, осуществляющих некоторые функциональные преобразования и связи между ними, то получим структурную схему в обобщенном виде, описывающую структуру системы. Структурные блок-схемы наглядны и вмещают в себя информацию о большом числе структурных свойств системы. На рис.3.1 показано для примера структурная схема системы менеджера качества, которая в виде модели представлена ГОСТ Р ИСО 9001-2001.

Рис.3.1 Структурная блок-схема системы менеджмента качества

- деятельность, добавляющая ценность продукции;

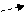- поток информации.

Графы структуры

Структурная блок-схема системы с трудом поддается формализации и анализу, поэтому для формализованного описания структурной системы и осуществления их математического анализа применяется теория графов.

3.1.Определение графов

Графом называют пару G=(А, В), где

А – множество вершин (элементов системы);

В – множество ребер (дуг) их соединяющих.

Различают следующие виды графов:

отмеченный граф – это граф с пронумерованными вершинами (обозначенными). Если граф отмечен, то ребро задается парой (i, j), в которой i и j – номера (имена) смежных вершин.

ориентированный граф – если все ребра графа заданы упорядоченными парами (i, j), в которых порядок расположения номеров смежных вершин имеют значение.

Геометрически графы изображают в виде диаграмм, на которых вершины отображаются точками (кружочками), а ребра – отрезками, соединяющими смежные вершины.

Ориентированное (i, j) задают отрезком со стрелкой, направленной из вершины i в вершину j ( i j ).

3.2.Построение графа по структурной схеме

Методика построения графа по структурной схеме проста: с вершинами графа сопоставляют блоки, а с ребрами связи между блоками. На рис.3.2 приведен граф, соответствующий блок-схеме, показанной на рис.3.1

Рис.3.2 Граф структуры системы менеджмента качества

Анализ структуры системы

Описание структуры системы в виде графа дает возможность провести анализ структуры системы и оценить ее качество. Рассмотрим следующие основные задачи анализа структур.

Анализ элементов

При исследовании структуры особое значение имеет выделение элементов, соответствующих изолированным, висячим и тупиковым вершинам графа. Изолированные вершины не инцидентны ни одному из ребер графа; висячие соответствуют вершинам, в которые нельзя попасть ни из одной другой вершины графа; тупиковые соответствуют вершинам, из которых нельзя попасть в другие вершины графа. В качестве примера рассмотрим граф на рис.4.1.

Рис.4.1 Фрагмент структуры системы

Граф на рис.4.1 содержит изолированную вершину 12, висячие вершины 1, 2, 3 и ни одной тупиковой вершины. Если соединить вершину 12 с вершинами 11 и 8, то она превратиться в тупиковую. Изолированные, висячие и тупиковые вершины на графе отыскиваются следующим образом:

Берется матрица смежности графа V = ||v_ij||;

По этой матрице для каждой вершины k (k = 1, 2, … , n), где n – число вершин в графе, определяется вектор v(k) = (v_k, v^k) с компонентами

v_k = 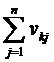, v^k = 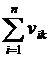, где

v_k – сумма элементов k-ой строки матрицы V, определяющее число ребер, выходящих из вершины k,

v^k – сумма элементов k-го столбца матрицы V, определяющее число ребер, входящих в вершину k

v_k = v^k = 0, то вершина k изолированная;

Если v_k = 0, то вершина k тупиковая;

v^k = 0, то вершина k висячая.

Что дает анализ элементов?

а. Наличие в графе изолированных вершин обычно свидетельствует об ошибках, допущенных при формировании или описании структуры, ведь система всегда целостный объект, все элементы которого взаимосвязаны;

б. Висячие вершины должны соответствовать входным элементам системы (вход системы);

в. Тупиковые вершины должны соответствовать выходным элементам системы (выход системы);

г. Через висячие и тупиковые вершины осуществляется процесс взаимодействия системы с внешней средой, поэтому очень важно, чтобы путем исследования графа они были правильно интерпретированы.

Анализ связи

Исследование связи между элементами структуры направлено, прежде всего, на выявление в соответствующем графе петель, контуров и сильносвязаных подграфов. Например, граф на рис.4.1 имеет петлю у вершины 11 и два контура, образованные ребрами, соединяющие вершины (4, 5, 6, 9) и (6, 9, 10, 11).

Подграф называется сильносвязным, если все входящие в него вершины взаимодостижимы, т.е. из любой вершины подграфа можно попасть в любую другую его вершину.

2.1.Выделение из графа сильносвязного подграфа

Пусть Q_i – множество вершин графа, достижимых из вершины , а Qⁱ – множество вершин графа, из которых можно достичь вершину .

Из определения сильносвязного подграфа следует, что пересечение множеств Q(i) = Q_i∩Qⁱ содержит вершины, принадлежащие одному сильносвязному подграфу, поэтому нахождение пересечения Q(i) равносильно определению сильносвязного подграфа, включающего в себя вершину .

Последовательно перебирая 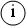и определяя множества Q(i) до тех пор, пока в эти множества не войдут все вершины графа, можно найти его разбиение на сильносвязные подграфы.

2.2.Пример определения сильносвязного графа

Для графа на рис.4.1 найдем его сильносвязные подграфы путем определения следующих пересечений множеств.

Q(1) = {1, 4, 5, 6, 9, 10, 11} ∩ {1} = {1}

Q(2) = {2, 5, 4, 6, 9, 10, 11, 7} ∩ {2} = {2}

Q(3) = {3, 7, 6, 9, 10, 11, 8} ∩ {3} = {3}

Q(4) = {4, 5, 6, 9, 10, 11} ∩ {1,…,11} = {4, 5, 6, 9, 10, 11}

Q(6) = Q(5) = Q(4)

Q(7) = {4, 5, 6, 7, 9, 10, 11,} ∩ {2, 3, 7, 8} = {7}

Q(8) = {8}

Теперь исходный граф можно разбить на сильносвязные подграфы: G(1), G(2), G(3), G(4), G(7), G(8), G(12), из которых только G(4) является нетривиальным (содержит больше одной вершины).

2.3.Граф-конденсация

Представим найденные сильносвязные подграфы как вершины нового графа, показанного на рис.4.2

Рис.4.2. Граф-конденсация

В результате получим граф, называемый конденсацией, который значительно проще исходного и в котором отсутствуют контуры и петли. Построение конденсаций рекомендуется для сложных структур, содержащих большое число элементов. Непосредственное исследование таких структур затруднено, а выделение конденсаций позволяет сосредоточить внимание на анализе существенных связей в наибольшей степени характеризующих особенности взаимодействия элементов системы.

Диаметр структуры

Если I и J – множество висячих и тупиковых вершин графа соответственно, то диаметр структуры определяется следующей формулой

d = 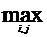d_ij,

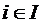
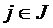, где

d_ij – длина минимального пути между висячей вершиной 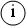и тупиковой вершиной 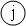равный числу ребер, составляющих этот путь.

Диаметр структуры характеризует максимальное число связей, разделяющих входные и выходные элементы структуры. По значению диаметра d можно косвенно судить о ряде предельных параметров системы, в частности о ее надежности, длительности, задержках сообщений, идущих от висячих вершин к тупиковым, инерционности. Определение значений d_ij сводится к стандартной задаче поиска кратчайшего пути на графе для каждой пары (i,j) такой, что , .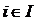

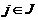Анализ структуры системы

Описание структуры системы в виде графа дает возможность провести анализ структуры системы и оценить ее качество. Рассмотрим следующие основные задачи анализа структур.

Связность

В теории графов под связностью графов понимается наименьшее число вершин, удаление которых из графов приводит а несвязному (содержащему изолированные вершины) или тривиальному (состоящему из одной вершины) графу. Используется также понятие реберной связности - наименьшего числа ребер, удаление которых приводит к несвязному или тривиальному графу. Обе характеристики достаточно сложно вычислить, еще сложнее дать им подходящую физическую интерпретацию, поэтому ограничимся только определением понятия «связность».

Степень централизации

Эта характеристика (критерий качества) структуры применяется для оценки неравномерности загрузки элементов структуры путем вычисления индекса центральности β. Пример показан на рис.4.3

Рис.4.3.а) связи в структуре распределены равномерно β = 0

Рис.4.3.б) структура с максимальной степенью централизации β = 1

Индекс центральности для неориентированного графа вычисляется по следующим формулам

β = (n-1)(2∙z_max-n)/z_max(n-2), где

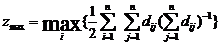
причем для всех i = j естественным образом длина минимального пути d_ij = 0

Сложность

Понятие сложности структуры с трудом поддается формализации и имеет субъективный оттенок. Сложность структуры будем определять сложностью анализа ее свойств. Если функционирование системы представить себе как процесс переработки входных воздействий в выходные, направленные соответственно от входных элементов системы к входным, то можно предположить, что изучать свойства этого процесса будет тем труднее, чем разнообразнее пути, ведущие от входа к выходу системы. Взяв это предположение за основу, показатель (критерий сложности) можно вычислить по следующей формуле.

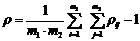
m₁ и m₂ – число висячих и тупиковых вершин в графе структуры;

ρ_ij –число различных путей, ведущих от i-ой висячей в j-ую тупиковую

Определение функций системы

Важнейшим понятием в системном анализе является понятие функции системы. Единого общепринятого определения функции нет. Анализ понятий функций, используемых в литературе, позволяет сгруппировать их по двум категориям:

1. включает определения, в которых функция идентифицируется с понятием «назначения объекта»;

2. ориентирована на рассмотрение функции как «зависимости».

Мы будем применять понятие функции, тяготеющее к первой категории – «назначение».

Функция – это проявление свойств системы (объекта) в виде действия или состояния.

В таблице 6.1. приведены примеры функций, выполненных различными объектами и процессами.

Табл.6.1

Объект (процесс)	Выполняемая функция
Экскаватор	Зачерпывать, транспортировать от забоя до отвала и выгружать грунт
Лампа	Освещать окружающий объект
Трансформатор	Изменять величину напряжения переменного тока
Сварка (склеивание)	Неразъемно соединять элементы
Упаковка	Предохранять продукцию при транспортировке и хранении

Описание функций

Различается качественное (словесное) и формализованное (математическое) описание функций. При проектировании системы стремятся к формализованному описанию. Формализованное описание функций обладает следующими преимуществами:

1. обеспечивается четкое определение самой функции;

2. устраняются потери важной информации при формулировании функций;

3. создается возможность автоматизации (компьютеризации) функционального анализа и синтеза системы, ускоряется процесс их проектирования.

Рассмотрим форму представления функций в порядке повышения степени их формализованного анализа.

3.1.Описание функции в слабо формализованном виде.

Такое описание представляет собой описание потребности в системе

F = P = (D, G, H, C) (6.1), где

Р – потребность в системе общепринятое и краткое описание на естественном языке назначения системы или цели ее существования;

D – действие, производимое системой и приводящее к желаемому результату, т.е. удовлетворению потребности;

G – описание объекта или предмета обработки, на которое направлено действие;

Н – описание особых условий и ограничений, при которых выполняется действие;

С – описание желаемых целей, к которым приводит (должно приводить) функционирование системы.

Возможно применение неполных образованных из формулы 6.1. описаний:

F = (D, G, H) (6.2)

F = (D, G) (6.3)

F = (D, H) (6.4)

Примеры описания функций (потребностей) приведены в табл. 6.2.

Словесное описание D, G и H приводит к неоднозначному пониманию функции разными специалистами, что затрудняет использование формулы (6.1) при автоматизации, поэтому предпочтительнее более формализованное описание функций.

3.2.Описание функций в более формализованном виде

Для более формализованного описания D, G и H в формуле (6.1) используются специальные словари, классификаторы, специальная терминология, установленная в данной предметной области. Например, в табл. 6.3. приведено такое описание двух виброзащитных систем (удалена компонента G – объект, на который направлено действие).

Табл.6.3

Наименование системы	D (действие)	H (условия)
Виброзащитная система 1	виброизоляция	В диапазоне частот 0,5-100 Гц твердых объектов массой до 100кг
Виброзащитная система 2	виброизоляция	В диапазоне частот 0,5-10 Гц продольных колебаний твердых объектов массой до 50кг

3.3.Описание функций на уровне физических операций

Описание функций отождествляется в данном случае с понятием физической операции

F = Q = (Am, E, Cm ) (6.5), где

Q – физическая операция;

Am, Cm – соответственно входной, выходной поток (фактор) вещества, энергии или сигналов;

Е – наименование операции по превращению Am в Cm (операция Коллера).

Описание в форме (6.5) отвечает на вопросы: «что (Am)», «как (Е)», «во что (Cm)» преобразуется с помощью функции F.

В таблице 6.4. приведены примеры описания функций в форме (6.5).

Табл.6.4

Наименование системы	Am (вход)	E (операция)	Cm (выход)
Светильник	Электрический ток	Преобразование	Световой поток
Электроплитка	Электрический ток	Преобразование	Теплота
Мельница	Зерно + механическая энергия	Соединение	Мука
Грузовой автомобиль	Топливо	Преобразование	Движение груза
Зеркало	Луч света	Изменение направления луча света	Отраженный луч света

Описание входного Am и выходного Cm потоков должно содержать следующую информацию:

а. наименование потоков вещества, энергии или символов, либо другого фактора;

б. качественную характеристику потока (фактора), например, для потока «электрический ток» качественная характеристика может означать переменный;

в. основную физическую величину, характеризующую поток (фактор), ее стандартное обозначение, единицу измерения;

г. количественную характеристику потока (фактора) – значение физических величин или диапазон их изменения.

Для описания компонент Е при описании функции в виде (6.5) используется таблица Коллера, в которой описано 12 пар операций, позволяющих формализовано описать физические процессы любой системы.

Табл.6.5

№ п/п	Прямая операция	Обратная операция
	Излучение	Поглощение
	Проводимость	Изолирование
	Сбор	Рассеивание
	Увеличение	Уменьшение
	Соединение	Разъединение
	Накопление	Выдача
	Изменение направления	Изменение направления

и т.д. 12 операций

Для более подробного формализованного описания функций используются более «тонкие» понятия:

а. физико-технический эффект;

б. физический принцип действия.

Эти понятия используются для описания физических законов и результатов их действия, они применяются при решении задач автоматизации технического творчества (решения изобретательских задач).

Истоки методологии SADT

SADT (Structured Analysis and Design) – методология структурного анализа и технического проектирования. Основное назначение SADT – облегчить описание и понимание искусственных сложных систем. Эта методология была предложена Дугласом Россом и сначала применялась в США (1969 – 1973) как методика системного проектирования программного обеспечения автоматизированных систем. Начиная с 1973г. сфера методологии САПР существенно расширилась: ее стали применять при проектировании аэрокосмических систем, в банковском деле и различных отраслях промышленности. В 1984г. эта методология министерством обороны США была стандартизирована и стала называться IDEF (Inteqrated DE Finition) и активно распространяется в Европе и Азии. С 1984г. IDEF вошла в семейство международных стандартов CALS и насчитывает сейчас около десяти модификаций. В данном курсе лекций нами будет использоваться модификация IDEF 0.

SADT-модель системы

SADT-модель системы – это набор взаимосвязанных диаграмм в виде древовидной структуры.

SADT-модель любой системы (процесса) строится в следующей последовательности: общая функция системы, указанная на верхней (корневой) диаграмме, последовательно детализируется на нижних диаграммах, каждая из диаграмм состоит из блоков и дуг. Блок графически изображается в виде схемы, показанной ранее в лекциях (рис.5.1) в виде упрощенной информационной модели процесса.

Блоки на SADT-диаграмме не располагаются случайным образом, а размещаются с учетом их важности (доминирования). Доминирование понимается как влияние, которое один блок оказывает на другие блоки. Наиболее доминирующий блок размещается в верхнем левом углу диаграммы, а наименее доминирующий – в правом нижнем углу. В одной диаграмме рекомендуется размещать не менее 3-х и не более 6-ти блоков. Дуги изображают связи между блоками. В SADT-диаграммах применяются следующие типы взаимосвязи блоков для описания их отношений:

1. Выход одного блока на вход другого или нескольких других блоков;

2. Обратная связь от выхода на вход этого блока или других блоков;

3. Выход одного блока на управление других блоков;

4. Обратная связь от выхода на управление этого или других блоков;

5. Выход одного блока на ресурсы других блоков;

6. Обратная связь от выхода на ресурсы этого или других блоков;

7. Один и тот же вход на несколько блоков;

8. Выходы нескольких блоков на выход одного блока;

9. Одно и то же управление на несколько блоков;

10. Один ресурс на несколько блоков.

Декомпозиция SADT-модели

SADT-модель развивается в процессе структурной декомпозиции сверху вниз.

Декомпозиция – это процесс создания диаграммы, детализирующей определенный блок и связанные с ним дуги.

Декомпозиция прекращается, когда нижний уровень достаточно детализирован для достижения цели моделирования (получены ответы на все поставленные вопросы).

SADT-диаграмма («потомки» с «родителями») стыкуется иногда с помощью кодов ICOM (по первым буквам английского алфавита): I – вход, C – управление, O – выход, М – ресурсы. На рис.7.1 показана схема декомпозиции SADT-диаграммы.

Анализ иерархии системы

Построение иерархии

Формируется решаемая проблема (задача). Для решения этой проблемы строится иерархия, включающая цель, расположенную в вершине (фокус), промежуточные уровни (критерии, процессы) и альтернативы (искомые решения), формирующие самый низкий иерархический уровень. На рис.8.2 в качестве примера приведена иерархия, построенная с целью определения значимости основных процессов организации с точки зрения удовлетворения нужд и ожидания всех заинтересованных сторон.

Рис.8.2. Иерархия для оценки значимости процессов организации

По международному стандарту ИСО 9004:2000 степень удовлетворенности всех заинтересованных сторон является глобальным критерием эффективности системы качества любой организации. Поэтому на рис.8.2 первый уровень иерархии (фокус) имеет одну цель: – эффективность и конкурентоспособность организации располагается на вершине иерархии (в фокусе), на втором (промежуточном) уровне располагаются заинтересованные стороны организации: – потребители; 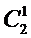– работники; 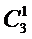– поставщики; 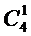– владельцы; 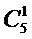– общество. На последнем (третьем) уровне иерархии располагаются альтернативы – основные группы (классы) существующих в организации процессов: 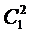– подразделения; 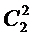– менеджмента качества; 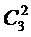– бизнес-процессов; 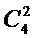– безопасности труда; – охраны окружающей среды. Целями третьего уровня являются удовлетворение нужд и ожиданий заинтересованных сторон, помещенных на втором уровне иерархии.

Рис.8.3. Иерархия задачи выбора оптимальной стратегии предприятия в области качества

Матрицы парных сравнений

Шкала отношений

Для определения оценок a_ij будем использовать шкалу отношений, представленную в виде таблицы 9.1. Данная шкала позволяет аналитику ставить в соответствие степеням предпочтения (доминирования) одного сравниваемого элемента иерархии перед другим некоторые числа от 1 до 9

Шкала отношений (степени значимости действий) Табл.9.1

Логический анализ систем

Логический анализ систем – это проведение исследований принципов построения систем методами математической логики. В основе такого анализа лежит понятие «формальная система».

2.1. Формальная система

Под формальной (дедуктивной) системой будем понимать совокупность четырех основных множеств (Т, Р, А, В) и двух дополнительных (Г, Д):

Ф = {<Т, Р, А, В> и <Г, Д>} (11.1)

а также четырех процедур П(Т), П(Р), П(А), П(В)

В этой формуле обозначены:

Т – множество базовых элементов, состоящее из элементов х, которые не могут быть расщеплены на более мелкие элементы. Например, буквы алфавита, слова из некоторого словаря, процессы, функции и т.п. Из базовых элементов будут строиться остальные элементы формальной системы. При этом декларируется, что существует процедура П(Т), которая за конечное число шагов должна дать положительный или отрицательный ответ на вопрос: «Является ли х элементом Т?».

Р – множество синтаксических правил, с помощью которых из элементов множества Т образуются синтаксически правильные совокупности, называемые «правильно построенные формулы» (ППФ). Например, из слов строятся синтаксически правильные фразы, из процессов формируются система менеджмента качества, из операций складывается процесс, из переходов складывается технологическая операция. При этом декларируется существование процедуры П(Р), с помощью которой за конечное число шагов можно получить ответ на вопрос: «Является ли совокупность х синтаксически правильно построенной формулой?».

А – множество аксиом, представляет собой подмножество ППФ произвольно выделенное из множества производных элементов формальной системы. Слово «аксиома» здесь не следует связывать с понятием истинности или ложности ППФ. При этом должна существовать процедура П(А), с помощью которой для любой ППФ можно получить ответ на вопрос о принадлежности ее к множеству А.

В – множество правил вывода, которые служат для того, чтобы с их помощью из множества аксиом можно было получить другие ППФ. Если имеется процедура П(В), с помощью которой можно определить для любой ППФ, является ли она выводимой, то соответствующая формальная система называется разрешимой. Правила вывода имеют общую форму записи

К => Q, (11.2) где

К – соответствует некоторой совокупности ППФ, которые либо принадлежат А, либо уже были получены из А с помощью правил вывода;

Q – совокупность ППФ, которые выводятся на данном шаге процесса вывода.

<Г,Д> – процедура интерпретации формальной системы, которая определяется двумя множествами;

Г{γ_i} – множество значений при интерпретации;

Д{γ_i} – множество правил интерпретации, где γ_i – значения (смысл), присваиваемые элементам множеств Т, Р, А, В (11.1) и элементам множества К и Q (11.2). Для решения задач логического моделирования в формальной системе применяются методы исчисления высказываний и методы исчисления предикатов.

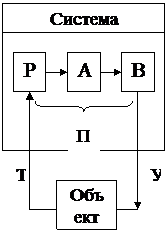
Пример интерпретации формальной системы

Рассмотрим пример интерпретации формальной системы при описании процесса управления. Систему управления объектом можно представить в виде схемы

Т – базовое множество информационных сигналов, поступающих от датчиков объекта;

Р – блок синтаксических правил, формирующих совокупности сигналов (по времени, по подобию и др.), необходимых для принятия решения;

А – блок аксиом, отображающих некоторые утверждения о соотношении значений сигналов, верные для всего периода функционирования объекта управления;

Классификация моделей

Рассмотрим кратко возможные методы математического моделирования систем. Прежде всего, введем классификацию моделей систем. Чаще всего классификация моделей систем основывается либо на природе связи между элементами в моделируемой системе (вещественные, энергетические и информационные модели), либо на способах моделирования (например, вероятностный или детерминированный, дискретные или непрерывные, с последействием или без последействия). Мы будем использовать классификацию методов моделирования систем в зависимости от усложнения (интеллектуализации) поведения моделируемой системы. Схема такой классификации приведена на рис. 11.1.

Рис.11.1 Классификация моделей систем

Схема классификации показана на рис. 11.1 является неполной, т.к. охватывает только наиболее распространенные виды моделей. Кроме того, между основными классами нет жесткой границы, они могут частично пересекаться. Рассмотрим основные классы моделей систем.

Задача принятия решений

Задача принятия решений содержательно может быть сформулирована следующим образом: «имеется множество вариантов решений (альтернатив), реализация каждой альтернативы приводит к наступлению некоторых последствий (исходов), анализ и оценивание исходов по набору показателей эффективности (критериев) однозначно характеризует альтернативы. Требуется, изучив предпочтения ЛПР, построить модель выбора альтернативы, лучшей в некотором конкретном смысле».

Морфологические таблицы

Морфологическое множество вариантов описания функциональных систем представляется морфологической таблицей на рис.15.1.

Рис. 15.1. Морфологическая таблица

В морфологической таблице (рис.15.1) цепочкой связанных альт