Плоское движение твердого тела.
Плоским называют такое движение тела, при котором все его точки движутся в плоскостях, параллельных заданной неподвижной. Проведем связанную с телом нормаль АА к заданной неподвижной плоскости и, как показано на рис. 13, двигаясь вместе с телом, через промежуток времени dt нормаль занимает положение A1А1. Очевидно, что все точки тела, лежащие на этой нормали, движутся одинаково, в частности, так же, как и точка O пересечения нормали с сечением тела плоскостью, параллельной заданной неподвижной. То же можно сказать о точках тела, лежащих на любой другой нормали. Поэтому для изучения плоского движения тела достаточно рассмотреть движение его сечения плоскостью, параллельной заданной, т.е. решить задачу кинематики в плоской системе координат.
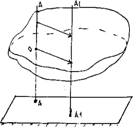
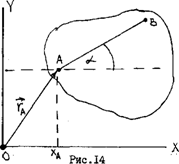
рис 13
Для определения положения сечения в пространстве в любой момент времени необходимо прежде всего задать положение произвольной точки А (полюса) этого сечения векторным или координатным способом. Кроме того, необходимо провести в сечении произвольную прямую АВ и указать угол a (альфа), который она образует с одной из осей координат (рис. 14). Движение сечения считается
заданным, если для любого момента времени известны зависимости:
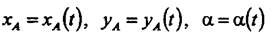
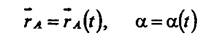 или
или
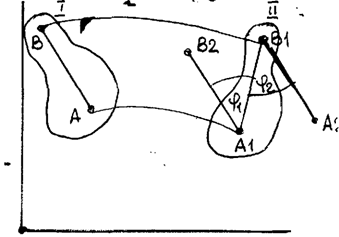 рис 15
рис 15
Соотношения (28), (29) задают кинематический закон плоского движения тела в векторном и координатном виде соответственно.
Осуществим плоское перемещение тела (его сечения) из положения 1 в положение 2 (рис. 15). В сечении выберем произвольную прямую AB. Выберем также в качестве полюса точку А. Если переместить сечение поступательно вместе с полюсом А, то полюс займет положение A1, а прямая АB - положение A1B2. Для приведения сечения в конечное положение 2 его необходимо повернуть вокруг полюса на угол j1. Таким образом, плоское перемещение тела можно рассматривать как одновременно происходящие поступательное перемещение вместе с полюсом и вращение вокруг этого полюса.
Если выбрать в качестве полюса точку B то после поступательного перемещения вместе с ним прямая AB займет положение A2B1. Для совмещения сечения с его конечным положением 2 его надо повернуть на угол j2. Следовательно, и в этом случае плоское перемещение можно представить как одновременно происходящие поступательное перемещение вместе с полюсом и вращение вокруг него. Очевидно, что и направление, и угол поворота в обоих случаях совладают. Поэтому кинематические характеристики поступательной части движения зависят от выбора полюса, а вращательной - не зависят.
7.1. Сила. ОПРЕДЕЛЕНИЯ:
Изменение состояния тела происходит в результате взаимодействий, которые приводят к изменению, как внутреннего состояния тел, так и состояния их движения. Количественной мерой взаимодействий, приводящих к изменению состояний тел, является сила.
Сила - векторная величина, она характеризуется следующими элементами: величиной, направлением в пространстве и точкой приложения силы.
Линия, вдоль которой направлена сила, называется линией действия силы.
Совокупность сил, приложенных к телу, называют системой сил.
Если под действием системы сил, приложенных к телу, оно может пребывать в состоянии покоя, система называется уравновешенной
Если одну систему сил, приложенных к телу, можно заменить другой, не изменяя его состояние, системы называются эквивалентными.
Сила, эквивалентная системе сил, называется равнодействующей этой системы.
Сила, равная по величине равнодействующей и противоположно ей направленная, называется уравновешивающей.
Силы взаимодействия между телами одной и той же системы называются внутренними.
Силы взаимодействия с телами, не входящими в состав данной системы называются внешними.
Силы, приложенные в одной точке тела, называются сосредоточенными.
Силы, приложенные ко всем точкам поверхности или объема тела, называются распределенными.
