Определение положения точки в пространстве.

Определение положения точки в пространстве.

Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени ука­зать ее местоположение координатным или векторным способом. Оба способа задания положения тела в пространстве эквивалентны, т.е. зная координаты точки, можно указать ее радиус-вектор, и наоборот. Из рис. 1 видно, что радиус-вектор представить можно 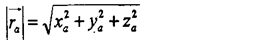диагональю прямоугольного параллелепипеда со сторонами, численно равными координатам точки Х_а, Y_a и Z_a. Отсюда очевидна связь модуля радиус-вектора точки с ее координатами:

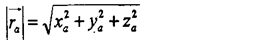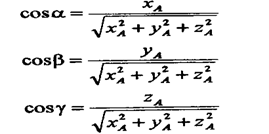Для определения направления радиус-вектора в пространстве можно определить углы a, b, g, которые радиус-вектор образует с координатными осями OX, OY, и OZ соответственно. Тогда:

Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4).

При движении точки ее координаты и радиус-вектор с течением времени изменяются, для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения.

ВЕКТОР ПЕРЕМЕЩЕНИЯ.

Для определения перемещения точки в пространстве вводят вектор перемещения.

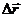
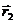
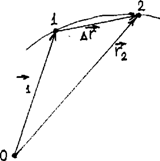
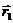Например, за промежуток времени Dt точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и ; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки.Наряду с изменением радиус-вектора точки происходит изменение ее координат, т.е. перемещение точки вдоль отдельных координатных направлений. Из рис.3 видно, что

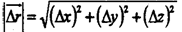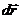
Вектор перемещения за конечный промежуток времени в общем случае не совпадает с направлением движения (направлением касательной к траектории движения). Очевидно, что эти направления будут совпадать в общем случае движения только для бесконечно малых перемещений точки .

ВЕКТОР СКОРОСТИ.

Вектором скорости называют вектор, определяющий быстроту и направление движения.

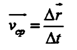Вектором средней скорости называют отношение вектора перемещения к промежутку времени, за который это перемещение происходит:

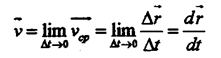Так как в произвольном случае движения вектор перемещения за конечный промежуток времени не определяет точно направление движения, это не может сделать и вектор средней скорости. Следо­вательно, необходимо рассматривать перемещения за бесконечно ма­лые промежутки времени.

Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:

Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость дви­жения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:

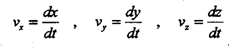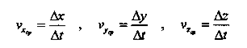
­ Компоненты же мгновенной скорости определяются как…

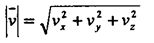Вектор скорости с его компонентами связан такими же по виду соотношениями, как радиус-вектор с

координатами точек:

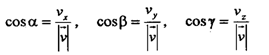
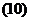2.2 ВЕКТОР УСКОРЕНИЯ.

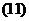Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора

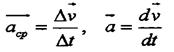скорости. Аналогично определени­ям для вектора скорости вводятся понятия среднего и мгновенного

ускорения:

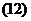При движении точки по произвольной траектории вектор изме­нения скорости ΔJ и, следовательно, вектор ускорения направлены в сторону вогнутости траектории независимо от того, увели­чивается или уменьшается величина скорости (рис. 4, 5):

Рис. 4. Ускоренное движение Рис. 5. Замедленное движение

Как видно из рисунков, в обоих случаях вектор dJ направлен в сторону вогнутости траектории. При ускоренном движении он отклоняется в сторону движения, при замедленном - в противоположную

Для определения мгновенного ускорения надо рассматривать бесконечно малые перемещения, т.е. векторы скорости J₁ и J₂ в соседних точках траектории. Поэтому вектор ускорения лежит в плоскости, содержащей касательную к траектории в данной точке и прямую, параллельную касательной в соседней точке траектории. Такая плоскость называется соприкасающейся. Поэтому наряду с представлением вектора ускорения компонентами

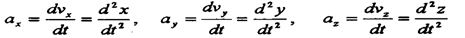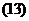можно рассматривать составляющие вектора в соприкасающейся плос­кости (т.е. только две компоненты). Для определения этих составляющих в любой точке траектории проводят соприкасавшуюся плос­кость и в ней две оси - нормальную O_n. в сторону вогнутости тра­ектории и касательную O_t по касательной к траектории. Изменение скорости и, соответственно, ускорение можно рассматривать в про­екциях на эти оси (рис. 6).

Двигаясь вдоль траектории, за промежуток времени Dt точка про­ходит путь DS скорость ее изменяется от J до J₁, при этом J₁ составляет угол Da (альфа) с осью O_t. По определению мгновенного ускорения:

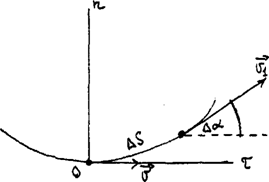Рис. 6

Преобразуем выражение предела, умножив и разделив его на Da и DS:

Отметим, что при Dt=0 бесконечно убывает и пройденный путь, и угол (DS=0, Da=0). При этом условии значения пределов равны:

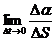Предел же называется кривизной траектории К. Кривизна траектории обратно

пропорциональна радиусу кривизны траектории:

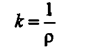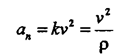С учетом этих замечаний выражение для нормальной составляющей вектора ускорения принимает вид

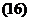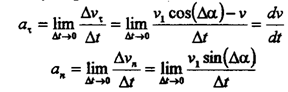
Для выяснения физического смысла ускорения рассмотрим два частных случая движения.

Равномерное криволинейное движение (V=const, k<>0). В этом случае, как видно из (14) и (16),

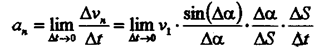
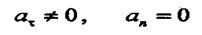Неравномерное прямолинейное движение (V<>соnst , K=0). При таком движении

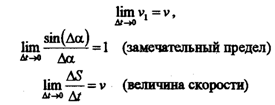
Следовательно, касательная составляющая ускорения определяет

изменение вектора скорости по величине, а нормальная - по направлению.

Кинематика твердого тела.

Для нахождения кинематического закона движения, т.е. r=r(t) или х = х(t), у=y(t), z=z(t) надо найти закон движения каждой точки тела, т.е. решить бесконечно большое число уравнений, что сопряжено с непреодолимыми математическими трудностями.

Однако особенности самого твердого тела и особенности его движения могут значительно упростить задачу.

ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ .

Числом степеней свободы называют число независимых механичес­ких координат полностью и однозначно определяющих положение тела в пространстве. Или: число независимых механических движений, которые одновременно может совершать тело.

Из таких определений следует, что число степеней свободы для свободной материальной точки равно 3. Для совокупности из n невзаимодействующих между собой точек число степеней свободы равно 3n.

Любые связи (взаимодействия) ограничивают число степеней сво­боды. Например, точка двигается по поверхности, задаваемой уравнением F(x,y,z)=0. В этом случае необходимо задать независимо 2 координаты, третья же не является независимой - она определяет­ся из уравнения поверхности, по которой движется точка. Иначе говоря, для точки, движущейся по поверхности, число степеней сво­боды равно 2. Для точки, движущейся вдоль линии, число степеней свободы равно 1. Действительно, любую линию можно пересечением двух поверхностей, т.е. для определения положения точки в пространстве нужно указать независимо только одну координату, две другие же определяются из уравнения линии.

Рассмотрим теперь систему точек, связанных жесткими связями. Пусть таких точек 2 (рис. 7). Для определения положения одной из точек системы в пространстве нужно указать 3 координаты, т.е. эта часть системы обладает 3-мя степенями свободы. Если эту точ­ку закрепить неподвижно, у системы будет отнято 3 степени свободы. Вторая точка при этом может двигаться только по поверхности сферы, т.е. обладает 2-мя степенями свободы. Следовательно, вся система обладает 5-ю степенями свободы.

Рис. 7 Рис. 8

Аналогично определяется число степеней свободы для системы, состоящей из трех жестко связанных между собой точек (рис. 8). Если одну из точек системы закрепить, у системы отнимается 3 степени свободы При закреплении второй точки дополнительно отнимается еще а степени свободы При этом третья точка сможет двигать­ся только вдоль линии, т.е. обладает одной степенью свободы. поэтому вся система обладает 6-ю степенями свободы. Легко убедиться» что добавляя к такой системе 4-ю, 5-ю и т.д. точки, мы не увеличим число степеней свободы, т.е. максимальное число степеней свободы для системы жестко связанных между собой точек равно. Абсолютно твердое тело как раз представляет собой такую систему, следовательно, обладает 6-ю степенями свободы.

3.3. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА.

Поступательным называют такое движение твердого тела, при котором любая прямая, проведенная в теле, при движении тела остается параллельной самой себе. Будем рассматривать движение абсолютно твердого тела. Выделим в теле произвольно т. т. А₁ и В₁. Через промежуток времени Dt они займут положения А₂ и В₂ соответственно (рис. 9).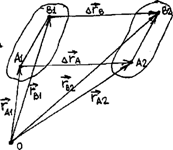

Рис. 9

Эти положения можно задать векторным способом, указав радиус-векторы r_a1, r_b1, r_a2, r_b2. Перемещения точек равны Dr_a, и Dr_b . Векторы (A₁B₁)и (A₂B₂) равны между собой, так как равны их модули (тело абсолютно твердое) и одинаковы направления (тело перемещается поступательно). Поэтому перемещения точек А и В равны (Dr_a = Dr_b) Поскольку точ­ки выбирались произвольно, можно сделать вывод, что при поступательном движении тела все его точки совершают одинаковые перемещения. По определению:

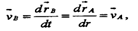
т.е. и скорости всех точек тела одинаковы. Аналогично можно пока­зать, что и ускорения всех точек тела одинаковы. Следовательно, при поступательном движении все точки тела движутся одинаково и для описания движения тела достаточно рассмотреть движение только одной его точки (чаще всего центра масс тела). Пример поступа­тельного движения - движение кузова автомобиля на прямолинейном участке дороги.

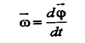4.ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ .

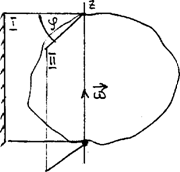Рис. 10

Вращательным называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными в пространстве. Прямая, проходящая через не­подвижные точки тела, называются осью вращения. При вращательном движении все точки тела движутся в параллельных плоскостях, описывая концентрические окружности, центры которых лежат на оси вра­щения.

Пусть тело вращается вокруг неподвижной оси Z (рис. 10). Для определения положения этого тела в пространстве через ось вращения проведем две плоскости: 1 - неподвижную и 2 - связанную с телом и вращающуюся вместе с ним. Положение тела задается углом j между плоскостями (угловой координатой). Изменение угловой координаты задает угловое перемещение Dj. Кинематический закон движения тела задан, если известна угловая координата в любой момент времени: j=j(t).

Быстрота вращения определяется угловой скоростью.

Средней угловой скоростью называют величину:а мгновенной:

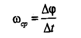для определения w как вектора необходимо угол поворота (угловое перемещение) также определять как вектор. Вектором угло­вого перемещения называют вектор, направленный вдоль оси вращения в ту сторону, откуда вращение тела видно происходящим против хо­да часовых стрелок. По такому определению вектор угловой скорос­ти

равен:

В случае вращения тела, показанном на рис. 10, вектор угловой скорости направлен вверх вдоль оси вращения.

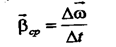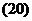Вектором среднего углового ускорения называют вектор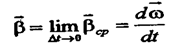

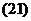а мгновенного

Легко видеть, что при ускоренном вращении твердого тела вектор углового ускорения направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости, а при замедленном - вдоль оси вращения противоположно вектору угловой скорости.

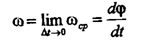
Постулаты Эйнштейна.

В основе специальной теории относительности, прежде всего, лежит факт постоянства скорости света в различных системах отсчета, что противоречит классическому закону сложения скоростей. Кроме того, нет никаких оснований считать, что механические опьггы позволят отличить одну инициальную систему отсчета от другой. Это позволило Эйнштейну сформулировать исходные постулаты специальной теории относительности.

Постулат о постоянстве скорости света: скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источника и приемника света.

Постулат относительности (общефизический принцип относительности): Никакими физическими опытами нельзя отличить одну инерциальную систему отсчета от другой. Наряду с этими постулатами Эйнштейн ввел принцип синхронизации часов, имеющий такое же значение в теории относительности, как и сформулированные выше постулаты.

Для того, чтобы одинаковые по устройству часы А и В (рис.31)

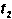
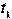шли одинаково, необходимо их синхронизировать. Пусть в момент времени , отсчитанный по часам А, в том месте, где они находятся, осуществляется световая вспышка. Сигнал от нее достигает часов В, мгновенно отражается и поступает к часам А в момент времени , отсчитанный по ним. Часы А и В считаются синхронизированными, если в момент отражения сигнала в т. В показания часов равны:

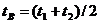
По сути дела в принципе синхронизации постулируется утверждение, что прямой и отраженный сигналы движутся с одинаковой скоростью, а само отражение происходит мгновенно, что не следует из сформулированных ранее постулатов.

Исходя из указанных постулатов, можно получить все основные выводы специальной теории относительности.

17.2. "Радиолокационный" метод (метод коэффициента "k ").

Движение тел можно графически представлять диаграммами x=x(t). В случае скоростей, сравнимых со скоростью света, масштаб х и t выбирается таким, что траектория светового сигнала ("световая линия") делит координатный угол пополам. Если же тело движется со скоростью, меньшей скорости света, угол наклона его траектории к оси t меньше 45°.

Предположим, что две инерциальные системы отсчета А и В находятся в относительном движении. Систему А условно считаем неподвижной. В исходный момент времени системы полностью совпадали. В этот момент осуществляется синхронизация подвижных и неподвижных часов и на них устанавливаются нулевые показания. Далее система В удаляется от А со скоростью v<c (рис.32).

Рис.32

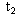
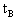
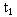Затем в системе А производится вторая вспышка в момент времени t, измеренный по часам А. Сигнал от нее догоняет систему В в момент времени , измеренный по часам В в подвижной системе, а показания неподвижных часов А для этого события равны . Сигнал мгновенно отражается и приходит в систему А в момент времени , отсчитанный по часам А.

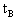
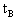Предположим, что показания подвижных часов в момент отражения сигнала в k раз отличаются от показаний неподвижных часов t в момент посылки сигнала:

= kt (148)

Системы равноправны, поэтому с момента отражения неподвижной можно считать систему В, а систему А - подвижной. Тогда показания часов А в момент приема сигнала равны:

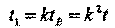
С момента синхронизации до отражения сигнала система В и световой сигнал, посланный в момент времени t (по часам А), проходят одинаковый путь:

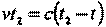
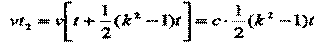т.е.

откуда получаем значение коэффициента k:

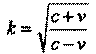Следовательно, показания подвижных часов в момент приема сигнала всегда больше показаний неподвижных часов в момент посылки сигнала:

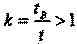Силы инерции.

Как уже отмечалось, существуют такие системы отсчета, в которых ускорение тел вызывается не только действием сил, но и самим движением системы отсчета.

Рассмотрим поведение свободного тела, находящегося в покое относительно неподвижной системы. В этой системе выполняются законы Ньютона: равнодействующая приложенных к телу сил равна нулю и тело, как следствие, находится в покое. Если же другая система отсчета движется относительно первой с ускорением a, то в подвижной системе тело получает ускорение - а, равное по величине ускорению системы и противоположно ему направленное. Следовательно, в подвижной системе законы Ньютона не выполняются: равнодействующая приложенных сил равна нулю, а тело приобретает ускорение.

Чтобы и в таких системах выполнялись законы Ньютона, приходится вводить дополнительные фиктивные силы, называемые силами инерции. В рассмотренном примере в подвижной системе вводится сила инерции:

объясняющая появление ускорения тепа в подвижной системе отсчета. Т.е. сила инерции равна произведению массы тела на ускорение системы и противоположно ему направлена.

Если связать систему отсчета с ускоренно движущимся телом, то геометрическая сумма всех сил, приложенных к телу, включая силу инерции, равна нулю (принцип Даламбера).

Силы инерции Кориолиса.

Пусть система вращается равномерно с угловой скоростью ω. Вдоль радиуса системы равномерно со скоростью v движется тело (рис. 36).

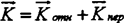Абсолютный импульс тела определяется относительным и переносным движением

Со временем будут изменяться обе составляющие абсолютного импульса. Рассмотрим сначала изменение относительного импульса.

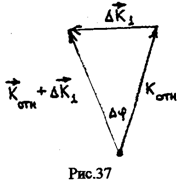Поскольку тело движется равномерно относительно подвижной системы, будет изменяться только направление импульса. За промежуток времени система (и ее радиус) поворачивается на угол Dj = wDt (рис. 37).

При малых углах поворота вращение относительного импульса равно:

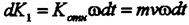Направлено это изменение в сторону вращения перпендикулярно к радиусу. Переносный импульс направлен все время в сторону вращения перпендикулярно к радиусу, величина его, пропорциональная линейной скорости вращения системы, зависит от удаления от центра вращения (рис.38)

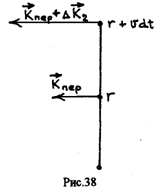Изменение величины переносного импульса за время dt равно

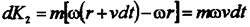Как видно, изменения относительного и переносного импульсов одинаковы по величине и направлению, поэтому полное изменение импульса тела равно

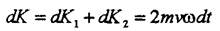С другой стороны, из основного закона динамики следует: , где F - равнодействующая приложенных к телу сил.

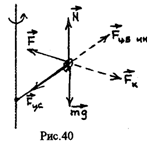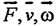Таким образом, наблюдаемые изменения импульса вызываются внешними силами, равными по величине:

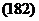F=2mnw

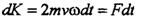
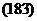Учитывая направления (рис. 39) векторов в векторном виде можно записать

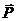
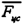
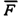
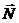
Для рассмотренного случая движения на рис.40 представим все действующие на тело силы. Пусть стержень вращается равномерно в горизонтальной плоскости, вдоль него равномерно движется небольшая муфточка. Относительно неподвижного наблюдателя на тело должны действовать следующие силы (отмеченные на рисунке сплошными линиями). Т.к. тело движется в горизонтальной плоскости, сила тяжести уравновешена реакцией стержня . Поскольку траектория тела криволинейная, на него должна действовать центростремительная сила , обеспечивающая нормальное ускорение. Наконец, на тело действует рассмотренная выше сила , приложенная со стороны стержня.

В системе, связанной с вращающимся стержнем, тело движется равномерно и прямолинейно, т.е. сумма приложенных к нему сил должна быть равной нулю. Как видно из рисунка, в горизонтальной плоскости силы не уравновешены, поэтому необходимо для выполнения законов динамики ввести силы инерции (на рисунке показаны пунктиром). Вдоль стержня действует центробежная сила инерции, уравновешивающая центростремительную силу.

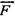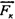Силу уравновешивает сила инерции Кориолиса :

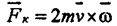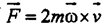
Как видно из (184), сила Кориолиса возникает во вращающейся системе отсчета при относительном движении тел. Исключением является движение тела вдоль оси вращения системы - силы инерции Кориолиса в этом случае не возникают.

Силы трения качения.

Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает

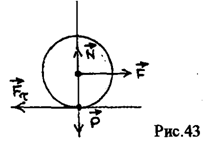
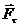сила препятствующая этому (рис. 43).

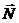Положим, что оба тела являются абсолютно твердыми, недеформируемыми, В этом случае нормальная составляющая реакции проходит через точку касания и центр масс катка (считаем его однородным симметричным телом, например, цилиндром). При такой модели любая по величине сила может вызвать качение катка, т.е. сопротивление движению.

не возникает. Более того, сила 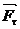должна вызывать угловое ускорение при любой по величине силе 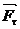, что противоречит опыту.

Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.

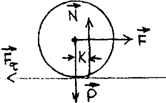Рис.44

Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра.

Положим, что сила 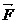вызывает равномерное качение катка, т.е.

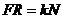
Откуда

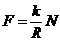(190)

Здесь 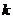(коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.

24. 1Вязкое трение

Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём.

Ньютон установил, что если под действием силы площадка 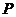площади 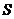движется равномерно со скоростью 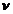относительно площадки 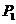(рис.45),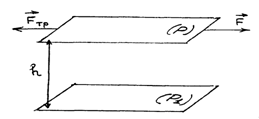

Рис.45

На подвижную площадку действуют силы сопротивления движению (силы вязкого трения):

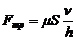
где 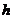- расстояние между площадками (слоями), 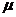- коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.

При движении тел в вязкой среде на них действуют силы сопротивления движению.

Стокс получил выражение для этих сил. При малых скоростях.

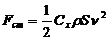(192)

где: 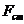- стоксова сила сопративления, 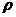- плотность среды, 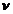- скорость тела, 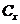-коэффициент, определяемый геометрией тела, 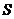- площадь проекции тела на плоскость, перпендикулярную направлению движения.

24.2Движение тел в сопротивляющейся среде.

При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорсти:

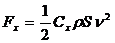
Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем:

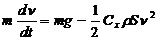
С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью 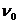. Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. Для этого сначала преобразуем (194):

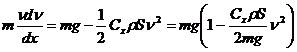
Обозначим: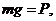

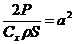
Тогда: 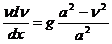Или: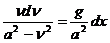

Интегрируя (195), получим: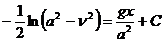

Константу интегрирования находим из начальных условий (x=0 и 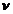=0):

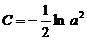
Подставив (197) в (196) получим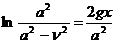

Или: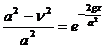

Откуда: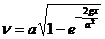

Через достаточно большой промежуток времени ( 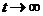) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно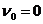

(178) и (179) и дают искомое решение поставленной задачи.

25.1 Упругие силы.

Упругостью называют свойство восстанавливать времменно утраченную форму и объём, а деформациями- само изменение формы и объёма тела. Причиной упругости является наличие одновременно присутствующих сил взаимодействия между частицами тела- притяжения ( 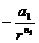) и отталкивания ( 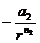). Равнодействующая этих сил равна:

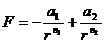(200)

На рис.46 представлены графики силы взаимного отталкивания (1), притяжения (2) и равнодействующая этих сил (3). На расстоянии 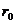между взаимодействующими частицами равнодействующая равна нулю (положение равновесия). При 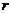< 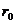преобладают силы отталкивания, а при 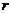> 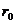силы притяжения.

Потенциальная энергия взаимодействия на расстоянии 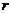между частицами:

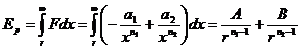(201)

где: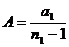

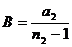
Графики потенциальной энергии сил отталкивания (1), притяжения (2) и равнодействующей (3) представлены на рис.47:

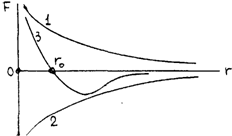
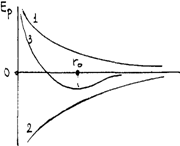
Рис.46 Рис.47

25.2Продольное сжатие и растяжение.

Закон Гука.

При продольном сжатии или растяжении одного упругого образца длинны 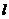и площади сечения 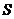удлинение образца 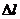определяется из опыта выражением:

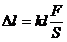(202)

где 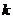- коэффициент упругости, определяемый свойствами материала образца.

Величина 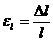называется относительной деформацией. Величина 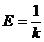, обратная коэффициенту упругости, называется модулем упругости Юнга.

С учётом этих обозначений закон Гука для деформации продольного сжатия или растяжения имеет вид:

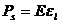(203)

где 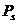- называется напряжением (отношение упругих сил в деформированном образце к площади его поперечного сечения).

При изменении продольных размеров одновременно и поперечные. Изменение 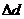диаметра 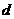образца (однородного цилиндра) также подчиняется закону Гука:

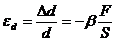(204)

где: 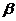-коэффициент поперечного сжатия при продольном растяжении.

Сравнивая (203) и (204) получим:

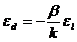(205)

Величина 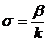называется коэффициентом Пуассона.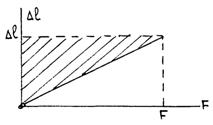

Рис.48

Если деформирующая сила изменяется от нуля до 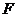, абсолютная деформация изменяется, соответственно, от нуля до 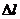то образец приобретает потенциальную энергию упругих деформаций, численно равную работе деформирующей силы. Эта работа равна площади заштрихованной фигуры (рис.48), т.е:

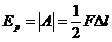
Используя закон Гука, получим:

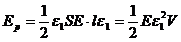
А плотность энергии, соответственно: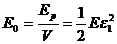

Деформация сдвига

Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила 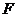, распределённая по грани площади