Стохастические модели управления запасами.
Рыночной среде присуща неопределенность, источником которой, в числе прочего, является произвольность и несогласованность решений рыночных агентов. В моделях управления запасами спрос, как правило, принимает случайные значения.
Случайный спрос характеризуется с помощью ряда распределения (дискретный спрос) или плотности вероятностей (непрерывный спрос). В данном пособии ограничимся рассмотрением дискретного случайного спроса. Непрерывный спрос в целях принятия решений можно представлять как дискретный.
Введем обозначения для показателей спроса, объемов запаса и частоты, с которой спрос принимает то или иное значение:
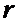 - значения спроса;
- значения спроса;
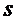 - показатели объема запаса;
- показатели объема запаса;
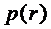 - частота, с которой спрос принимает соответствующее значение.
- частота, с которой спрос принимает соответствующее значение.
Издержки хранения запаса возникают при условии 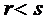 (запас превышает спрос). Штрафы за дефицит возникают при условии
(запас превышает спрос). Штрафы за дефицит возникают при условии 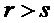 (спрос превышает дефицит).
(спрос превышает дефицит).
Поскольку соотношения между спросом и запасом становятся случайными, случайной величиной становится и значение издержек. Иными словами, в стохастических моделях минимизации подлежит математическое ожидание функции затрат:
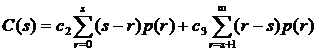
В теории управления запасами доказано, что математическое ожидание затрат, связанных с формированием и поддержанием запаса минимально при оптимальном размере запаса 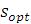 , который удовлетворяет соотношению
, который удовлетворяет соотношению 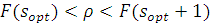 . В данном соотношении
. В данном соотношении 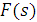 - функция распределения вероятностей, которая показывает частоту, с которой в ряду распределения случайная величина принимает значение меньшее, чем данное.
- функция распределения вероятностей, которая показывает частоту, с которой в ряду распределения случайная величина принимает значение меньшее, чем данное.
Рассмотрим определение оптимального размера запаса на примере. Предположим, предприятие приобретает агрегат с запасными блоками к нему. Стоимость одного блока 5 д.е. В случае выхода агрегата из строя из-за поломки блока убытки от простоя и расходы на срочный ремонт составят 100 д.е. Статистика эксплуатации аналогичных агрегатов представлена в виде таблицы, характеризующей ряд распределения (табл. 34).
Таблица 34 . Ряд распределения агрегатов по числу заменяемых блоков.
Число замененных блоков, 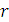 | |||||||
Доля агрегатов в выборке, которым потребовалась замена 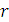 блоков, блоков, 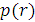 | 0,90 | 0,05 | 0,02 | 0,01 | 0,01 | 0,01 | 0,00 |
Решение основано на вычислении плотности убытков и определении значений функции распределения вероятностей. Так как 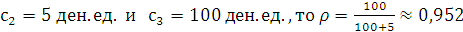 . Значения функции распределения вероятностей представлены в таблице 35.
. Значения функции распределения вероятностей представлены в таблице 35.
Таблица 35 . Функция распределения вероятностей.
Число замененных блоков, 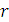 | |||||||
Доля агрегатов в выборке, которым потребовалась замена 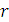 блоков, блоков, 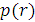 | 0,90 | 0,05 | 0,02 | 0,01 | 0,01 | 0,01 | 0,00 |
Функция распределения вероятностей 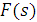 | 0,9 | 0,95 | 0,97 | 0,98 | 0,99 |
На основании проведенных вычислений определяем 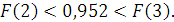 Следовательно,
Следовательно, 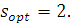
Раздел 7. Основы теории систем массового обслуживания.
Основные понятия теории систем массового обслуживания.
Практически любую хозяйственную деятельность можно рассматривать в виде системы, обслуживающей запросы потребителей – как внешних, так и внутренних по отношению к фирме (предприятию). Система массового обслуживания представляет собой систему, в которой возникают массовые запросы на выполнение каких-либо услуг ( работ) и происходит удовлетворение этих запросов. Она включает в себя следующие элементы: а) входящий поток требований (заявок); б) очередь; в) обслуживающие устройства (каналы обслуживания); г) выходящий поток требований.
Системы массового обслуживания (СМО) могут быть классифицированы по ряду признаков. Так, в зависимости от условий ожидания начала обслуживания выделяют: 1) СМО с отказами; 2) СМО с ожиданием (очередью). В СМО с отказами заявки, поступающие в систему в момент, когда все каналы обслуживания заняты, получают отказ и теряются. В СМО с ожиданием в такой же ситуации заявка становится в очередь (ограниченную или неограниченную) и ожидает начала обслуживания до тех пор, пока не освободится один из каналов.
По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.
В данном пособии будем рассматривать такие задачи теории СМО, в которых входящий поток требований является простейшим (пуассоновским). Простейший поток обладает тремя основными свойствами:1)ординарностью;2)стационарностью;3)отсутствием последействия. Ординарность потока означает практическую невозможность одновременного поступления в систему двух и более требований. Стационарным называется поток, для которого математическое ожидание числа требований, поступающих в систему в единицу времени, не меняется во времени. Отсутствие последействия означает, что число требований, поступивших в систему до определенного момента, не определяет того, сколько требований поступит в будущем.
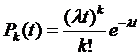 В простейшем потоке частота поступления требований в систему подчиняется закону Пуассона, который гласит, что вероятность поступления в систему за время
В простейшем потоке частота поступления требований в систему подчиняется закону Пуассона, который гласит, что вероятность поступления в систему за время 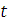 ровно
ровно 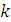 требований определяется по формуле
требований определяется по формуле
где 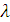 - интенсивность поступления потока заявок, то есть число заявок, поступающих в систему в единицу времени.
- интенсивность поступления потока заявок, то есть число заявок, поступающих в систему в единицу времени.
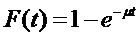 Важная характеристика СМО – время обслуживания заявки. Время обслуживания одной заявки является величиной случайной и описывается законом распределения. Наибольшее распространение в практических приложениях теории СМО получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид
Важная характеристика СМО – время обслуживания заявки. Время обслуживания одной заявки является величиной случайной и описывается законом распределения. Наибольшее распространение в практических приложениях теории СМО получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид
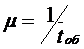 В данной формуле
В данной формуле 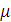 - интенсивность обслуживаний, то есть количество заявок, обслуженных в единицу времени, которое можно определить как единицу, деленную на среднее время обслуживания одной заявки
- интенсивность обслуживаний, то есть количество заявок, обслуженных в единицу времени, которое можно определить как единицу, деленную на среднее время обслуживания одной заявки
Смысл функции распределения времени обслуживания состоит в том, что она показывает вероятность того, что время обслуживания не превосходит величины 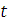 .
.
