Задача распределения ресурсов.

Рассмотрим ситуацию, в которой необходимо распределить некий ограниченный запас ресурса между пользователями или направлениями использования. Из всех возможных альтернатив распределения необходимо выбрать такую, которая обеспечит максимум полезного эффекта лицу или лицам, принимающим решение.

Предположим, некая корпорация распределяет 100 ден. ед. инвестиционных ресурсов между 4-мя подразделениями. В каждом подразделении на альтернативной основе можно выбрать для реализации один из 5-ти инвестиционных проектов, стоимость каждого из которых кратна 20. Известен прирост объема продаж, достигаемый в результате реализации соответствующего проекта в каждом подразделении. Требуется выбрать вариант распределения инвестиционных ресурсов, максимизирующий суммарный прирост объема продаж.

При решении задач такого типа в качестве шага процесса принятия решения следует рассматривать выделение той или иной суммы ресурсов конкретному подразделению. Последовательность шагов логическая, а не хронологическая. Ясно, что в данной ситуации очередность не важна. Управляемой системой является запас ресурса. Множество состояний системы будет характеризоваться конкретными вариантами распределения инвестиционных средств между получателями. Дадим содержательную трактовку другим ключевым понятиям метода динамического программирования в привязке в условиям данной задачи.

Множество состояний 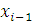- возможные варианты остатка запаса инвестиционных средств перед выделением его 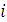-му подразделению. Поскольку возможны варианты распределения средств (от 0 до 100 ден. ед.) в кратных 20-ти суммах, то состояния системы пред 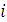-м шагом могут характеризоваться величинами: 0,20,40,60,80,100.

Принимаемое на 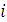-м шаге решение будет зависеть от остатка запаса, а потому оно может характеризоваться определенным набором элементов множества 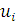. Данное множество образуют величины 0,20,40,60,80,100. Множество состояний 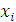– возможные варианты остатка запаса средств после их выделения 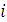- му подразделению. Возможные величины остатков, как можно предположить, также 0,20,40,60,80,100.

Целевая функция 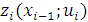отражает прирост объема продаж в 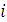-м подразделении при условии, что величина остатка средств перед выделением ему выбранной из множества 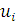суммы определялась элементом множества 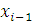. Выражение 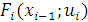означает максимальный суммарный прирост объема продаж, полученный в подразделениях, от 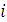-го до 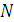-го включительно, при условии, что перед выделением ему суммы из множества 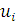остаток средств характеризовался соответствующим элементом множества .

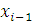В таблице 15 отражены показатели прироста объема продаж в каждом из 4-х подразделений в зависимости от величины выделенных инвестиций.

Таблица 15. Эффект инвестиций в подразделениях корпорации

	Прирост объема продаж (ден. ед.)
Инвестиционные затраты (ден. ед.)	1-ое подразделение	2-ое подразделение	3-е подразделение	4-е подразделение

Таким образом, решение основано на анализе 4-х шагов, осуществляемом вначале в обратном порядке (условная оптимизация), а затем в прямом (безусловная оптимизация). Хотя очередность подразделений в данном случае не важна, договоримся, что номер шага будет соответствовать номеру подразделения, указанному в таблице 15. Следовательно, первым шагом будет выделение средств 1-ому подразделению, вторым – 2-ому, третьим – 3-ему, четвертым – 4-ому.

Условная оптимизация начинается с анализа 4-го шага (табл. 16). Прокомментируем подход к его реализации.

Перед заключительным шагом процесса варианты остатка средств – элементы множества 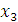, могут быть нулевыми или суммами, кратными 20-ти. Остаток целиком выделяется последнему получателю, поэтому каждому элементу множества 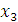соответствует только одна альтернатива среди элементов множества 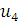, что обеспечивает условно-оптимальное значение целевой функции, в точности совпадающее с показателями .

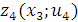Таблица 16. Анализ 4-го шага.

x3	u4		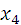Z4	F4

Результаты, достигнутые на 4-ом шаге, используются в таблице для анализа 3-го шага (табл. 17) в виде элементов множества 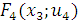. Важным отличием 3-го шага от заключительного является наличие альтернатив принятия решения для элементов множества 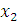(за исключением 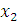=0). Действительно, наличие определенного остатка средств создает спектр возможностей – либо ничего не выделить третьему получателю, либо выделить сумму, кратную 20-ти. Выбор варианта решения определяет значение остатка средств после выделения их 3-ему подразделению

( элементы множества 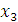), а также эффект в виде прироста объема продаж в третьем подразделении 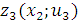. Суммируя эффект, достигаемый на 3-ем и 4-ом шагах, определяем по максимальной сумме условно-оптимальное значение целевой функции .

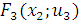Следует заметить, что целевая функция достигает условно-оптимального значения в отношении одного и того же элемента множества 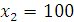при разных альтернативах. Ни одну из этих альтернатив нельзя исключать из последующего анализа! В некоторых ситуациях (но не в данной) оптимальное распределение, доставляющее целевой функции одно и то же экстремальное значение, не единственно.

Таблица 17. Анализ 3-го шага.

x2	u3	x3	Z3	F4	Z3+F4	F3
						-
						- -
						- - -
						- - - -
						- - - -

Приведенные выше рассуждения справедливы для 2-го и для 1-го шагов.

Ниже представлена характеристика 2-го шага (табл. 18), на котором рассматривается выделение инвестиционных средств второму получателю. Результат реализации данного шага – определение условно- оптимальных значений целевой функции на шагах от 2-го до 4-го включительно ( элементы множества 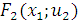, отраженные в последней колонке таблицы 18).

Таблица 18. Анализ 2-го шага.

x1	u2	x2	Z2	F3	Z2+F3	F2
						-
						- -
						- - -
						- - - -
						- - - - -

По завершении анализа 1-го шага (табл. 19) оказалось выявлено максимальное значение суммарного прироста объема продаж – 85 ден. ед. Таким образом, условная оптимизация закончена. Ее результатом является, как и ожидалось, экстремальное значение целевой функции:

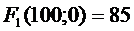
Следовательно, существует некий оптимальный вариант распределения инвестиционных средств между четырьмя подразделениями, который может обеспечить корпорации 85 ден. ед. прироста объема продаж.

Таблица 19. Анализ 1-го шага.

x0	u1	x1	Z1	F2	Z1+F2	F1
						-
						- -
						- - -
						- - - -
						- - - - -

Теперь осуществляем движение в прямом направлении, рассматривая таблицы в обратном порядке, с тем чтобы получить оптимальное распределение инвестиционных средств.

В таблице 19 экстремальное значение целевой функции 85 соответствует 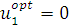. Иными словами, первому получателю средств выделять не следует, и запас в 100 ед. целиком остается для последующего распределения. В таблице 18 находим 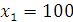и определяем альтернативу решения, которая соответствует условно-оптимальному значению целевой функции: 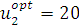. То есть, второму получателю следует выделить 20 ден. ед. инвестиционных средств. Остается 80 ден. ед. запаса. В таблице 17 находим 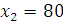и определяем альтернативу решения, которая соответствует условно-оптимальному значению целевой функции: 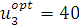. Третьему получателю надлежит выделить 40 ден. ед. запаса. Естественно, остаток 40 ден. ед. должен быть выделен четвертому получателю: 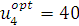. В итоге вектор оптимальных управлений будет иметь следующий состав .

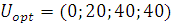4.4. Задача определения оптимальной политики замены оборудования.

Рассмотрим общую постановку задачи замены оборудования. В рамках планового периода, охватывающего N лет, необходимо определить оптимальные сроки замены оборудования возрастом не старше t лет, с тем чтобы суммарная прибыль от эксплуатации оборудования была максимальной. Для принятия решения имеются следующие данные: 1) годовой доход, получаемый от эксплуатации оборудования соответствующего возраста - 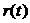; 2) годовые затраты на эксплуатацию оборудования соответствующего возраста - 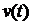; 3) ликвидационная стоимость единицы оборудования - 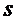; 4) цена приобретения единицы нового оборудования - 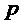Решение принимается в начале каждого года планового периода.

Дадим содержательную интерпретацию основных понятий метода динамического программирования для данной задачи. Управляемой системой является возраст оборудования. За шаг процесса в данном случае целесообразно принять год планового периода. Под состоянием оборудования подразумевается его возможный возраст. 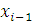– множество состояний оборудования перед 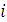-м годом. Его элементами будут числа 1,2,…,t . 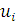– множество решений в отношении оборудования, которые могут быть приняты в начале 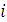-го года. Элементы его следующие:1) оборудование сохранить ; 2)оборудование заменить, реализовав старое по остаточной стоимости 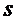и приобретя новое по цене .

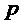В данной задаче целесообразно различать два множества состояний оборудования: 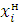- множество состояний сразу после выбора управления в 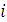-м году и 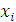– множество состояний в конце 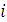-го года, когда возраст оборудования становится больше на 1 год.

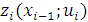- прибыль в 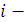м году в использования оборудования; 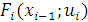– условно-оптимальная прибыль от использования оборудования в период с 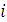-го по N-й год при условии, что перед 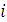-м годом возраст оборудования характеризовался элементом множества 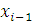и в начале 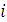-го года было принято некоторое управление из множества .

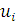Если в начале года выбрано «сохранение», то годовая прибыль от эксплуатации оборудования выражается разностью

,

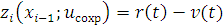если выбрана «замена», то прибыль считается по формуле

.

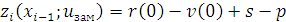Условно-оптимальное значение целевой функции 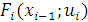определяется наибольшим из выражений. Если же оба управления приводят к одному и тому же результату, то целесообразно выбрать «сохранение», так как знакомое оборудование проще эксплуатировать.

Развернем вначале процедуру условной оптимизации, начав ее с последнего года планового периода. По завершении условной оптимизации пройдем процесс в прямом направлении и сформируем оптимальную политику сохранения и замены оборудования.

Рассмотрим задачу следующего содержания. Определить оптимальную политику по отношению к оборудованию возраста не старше 6 лет на плановый период в 4 года. В таблице 20 даны значения годового дохода 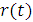и эксплуатационных расходов v(t) в зависимости от возраста оборудования t.

Таблица 20. Исходные данные задачи.

t
r (t)
v (t)
z

Ликвидационная стоимость старого оборудования S = 4 ден. ед.; цена единицы нового оборудования P = 13 ден. ед. Предположим, что все указанные в качестве исходных данных показатели не меняются в течение четырех лет

Условную оптимизацию начинаем с анализа 4-го года периода (табл. 21).

Таблица 21. Анализ 4-го шага.

x3	u4	x4н	Z4	F4
	Сохранение Замена			-
	С			-
	С			-
	С			-
	С			-
	С			-

Условная оптимизация двухлетнего периода, состоящего из 3-го и 4-го годов, приводится в таблице 22.

Таблица 22. Анализ 3-го шага.

x2	u3	x3н	Z3	x3	F4	Z3+F4	F3
	C						-
	C						-
	C						-
	C						-
	C						-
	C			-	-	-	-

В остальных таблицах укажем лишь строки, соответствующие условно-оптимальным управлениям ( табл. 23 и табл 24).

Таблица 23. Анализ 2-го шага.

x1	u2	x2н	z2	x2	F3	z2+F3	F2
	C C

Следует обратить внимание на отличие состава элементов множества 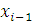в заключительной таблице. В множестве 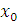имеется элемент 0. Наличие оборудования нулевого возраста перед началом планового периода объясняется тем, что за рамками планового периода какие-то единицы оборудования было решено заменить, и данное решение было реализовано, то есть старое оборудование продано по остаточной стоимости и новое оборудование приобретено. Следовательно, для этой группы оборудования разница 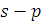не должна влиять на решения, принимаемые в рамках рассматриваемого четырехлетнего периода.

Таблица 24. Анализ 4-го шага.

x0	u1	x1н	z1	x1	F2	z1+F2	F1
	C C C C

По завершении условной оптимизации составим матрицу максимальных прибылей, куда включим данные последних столбцов таблиц 21-24. По матрице (табл. 25) достаточно просто определить оптимальную политику на 4 года для оборудования любого возраста, не превышающего 6 лет.

Таблица 25. Матрица для проведения безусловной оптимизации.

Возраст оборудов., t	Максимальная прибыль по годам планового периода
1-4	2-4	3-4
		-	-	-

Курсивом выделены элементы в «области сохранения», обычным шрифтом – в «области замены». Определим, к примеру, оптимальную политику в отношении оборудования, которое имело к началу планового периода возраст 4 года. На пересечении первого столбца и пятой строки (t =4) находим элемент 33, который попадает в область замены. К началу второго года, следовательно, мы будем иметь новое оборудование возраста 1 год, которому соответствует элемент 30 в области сохранения. К началу третьего года возраст данного оборудования составит 2 года и его следует сохранить. К началу 4-го года оборудованию будет 3 года и его следует сохранить. Таким способом можно определить вектор оптимальных управлений для оборудования любого возраста в рамках рассматриваемого четырехлетнего периода.