Теория двойственности в линейном программировании

Каждая задача линейного программирования имеет двойственную ей задачу. Двойственную задачу можно наделить вполне определенным смыслом.

Рассмотрим в качестве исходной задачу определения оптимальной производственной программы (симметричную на максимум целевой функции).

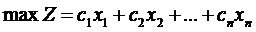
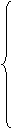
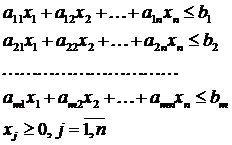
Предположим, предприятие, разрабатывающее программу, рассматривает в качестве альтернативы продажу ресурсов. При каких условиях реализация данной альтернативы станет возможной? Определить данные условия можно, решив задачу следующего содержания:

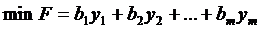
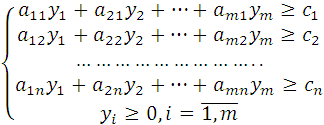
В данной задаче: 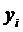- условные (маржинальные) цены ресурсов, характеризующие изменение выручки предприятия при изменении запаса ресурса на единицу:

.

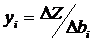Целевая функция задачи характеризует основания выбора решения о приобретении ресурсов покупателем. Покупатель стремится минимизировать расходы на покупку запасов .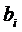

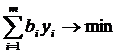
Ограничения характеризуют основания выбора решения продавцом, то есть предприятием. Предприятие желает получить от продажи ресурсов доход, не меньший, чем доход от продажи продукции по ценам 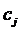. В каждом ограничении сопоставляется оценка ресурсов, требуемых для выпуска единицы изделия, с ценой продажи единицы изделия.

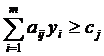
Для составления каждого неравенства коэффициенты 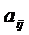(нормы расхода ресурсов) отбираются по второму индексу, обозначающему номер продукта. Данная задача является двойственной по отношению к задаче определения оптимальной производственной программы. Двойственная задача, как видно, также имеет симметричную запись. Вполне правомерно говорить о существовании пары взаимно двойственных симметричных задач.

На базе сопоставления форм записи обеих задач можно вывести следующие правила построения симметричных двойственных задач:

1) если целевая функция прямой задачи максимизируется, то двойственной – минимизируется, и наоборот;

2) числу ограничений прямой задачи равно число переменных двойственной задачи;

3) числу переменных прямой задачи равно число ограничений двойственной задачи;

4) для получения ограничений двойственной задачи необходимо транспонировать матрицу коэффициентов 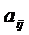прямой задачи;

5) в двойственной задаче знак ограничений-неравенств противоположен знаку ограничений-неравенств прямой задачи;

6) переменные двойственной задачи неотрицательны.

Рассмотрим две возможности использования теории двойственности: 1) для рационализации решения задач, симметричных на минимум целевой функции; 2) для проведения анализа оптимальной производственной программы.

Трансформация записи задачи, симметричной на минимум целевой функции, не обеспечивает получения первоначального неотрицательного базисного решения.

В исходном пункте мы располагаем следующей записью:

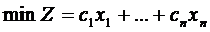
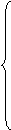
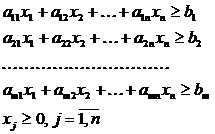
При трансформации записи в каноническую система линейных уравнений принимает следующий вид:

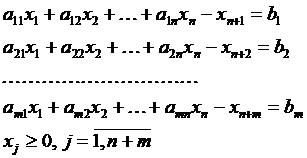
Следовательно, матрица системы уже не будет содержать в своем составе единичную матрицу как подсистему:

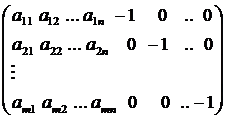
Ранее рассматривались возможности получения начального неотрицательного базисного решения либо с помощью преобразований матрицы, либо с помощью искусственных переменных. Теория двойственности открывает еще одну возможность - составить двойственную задачу и решить ее симплекс-методом. В соответствии с доказанными теоремами двойственности, если одна из пары двойственных задач имеет оптимальное решение, то его имеет и другая задача. Экстремальные значения целевых функций задач совпадают

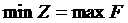, а оптимальные значения переменных исходной задачи определяются по правилу соответствия (рис. 3) в индексной строке заключительной симплексной таблицы.

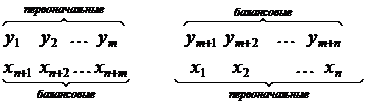
Рис. 3. Соответствие между переменными прямой и двойственной задач.

Следует отметить, что данная схема фиксирует именно соответствие между переменными, а не тождество их значений. Справедливым является следующее утверждение: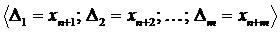

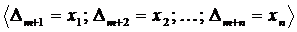
Двойственные оценки ресурсов 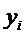находят применение в так называемом постоптимизационном анализе, так как они являются маржинальными ценами ресурсов

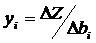. Это позволяет принимать решения о перспективах изменения запаса соответствующего ресурса в следующем плановом периоде. Кроме того, значения 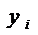позволяют судить о дефицитности ресурсов. Если 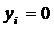, то ресурс бездефицитен, то есть его запас избыточен; если 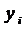положительна, то запас ресурса используется полностью.

Двойственные оценки можно также использовать при принятии решений о целесообразности расширения ассортимента. Предположим, поступило предложение о расширении ассортимента выпускаемых изделий за счет дополнительного продукта. Цена данного продукта 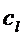, а нормы расхода ресурсов 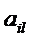. Определим оценку ресурсов, требуемых для выпуска единицы нового изделия, и сравним ее с ценой продажи изделия. Расширять ассортимент выгодно, если

< .
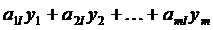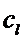