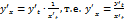Производная функция (определение, правило непосредственного нахождения производных)

Производной функцией 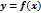в точке x₀называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

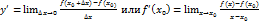
Производная функции f(x) есть некоторая функция f’(x), произведенная из данной функции.

Функция 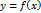, имеющая производную в каждой точке интервала (a;b) называют дифференцируемой в этом интервале. Операция нахождения производной функции называется дифференцированием.

Значение производной функции 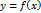в точке x=x₀ обозначается одним из символов: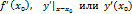

Правило непосредственного нахождения производных:

· аргументу 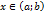дадим приращение ;

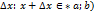· найдем соответствующее приращение функции: ;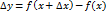

· составим отношение приращения функции к приращению аргумента: ;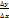

· найдем предел этого отношения при .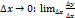

Если этот предел существует, то его называют производной функцией f(x) и обозначают одним из символов: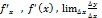

44. *Геометрический и механический смысл производной.

45. *Связь между непрерывностью и дифференцируемостью функций

46. *Основные теоремы о производных

Теорема(производная суммы) : Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: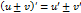

Теорема(производная произведения) :

Теорема(производная частного) :

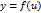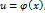Пусть и тогда 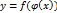- сложная функция с промежуточным аргументом u и независимым аргументом х

Теорема(производная сложной функции) :

Если функция 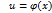имеет производную 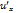в точке х, а функция у = f(u) имеет производную у'_и в соответствующей точке 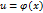, то сложная функция 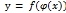имеет производную 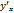в точке x₁, которая находится по формуле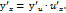

Теорема(производная обратной функции) :

Если функция 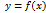строго монотонна на интервале (a;b) и имеет неравную нулю производную 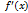в произвольной точке интервала, то обратная ей функция 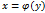также имеет производную 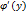в соответствующей точке, определяемую равенством 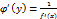или .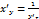

Дифференцирование функций, заданных неявно и параметрически.

Задана неявно:

Если функция задана уравнением у = f(x), разрешенным относительно y, то функция задана в явном виде.

Под неявным заданием функции понимают задание функции в виде уравнения 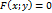, не разрешенного относительно y.

Алгоритм:

1) Дифференцируем заданное уравнение F(x,y)=0 по х, учитывая что х – независимая переменная, у – ее функция.

2) Результат дифференцирования разрешаем относительно искомой производной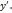

Задана параметрически:

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений: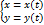

Найдем производную 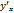, считая, что функции имеют производные и что функция x=x(t) имеет обратную 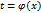. По правилу дифференцирования обратной функции получаем: .

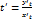Функцию y=f(x) определяемую параметрическими уравнениями, можно рассматривать как сложную функцию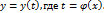

По правилу дифференцирования сложной функции имеем: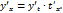

Получаем: