Центр тяжести пирамиды лежит на прямой, соединяющей центр тяжести основания с вершиной, на расстоянии 1/4 длины этой линии, считая от основания

Раздел 2. «КИНЕМАТИКА»

1. Что называется траекторией точки? Какое движение точки называется прямолинейным? Криволинейным?

Линию, вдоль которой движется материальная точка, называют траекторией.

Если траектория — прямая линия, то движение точки называют прямолинейным; если траектория — кривая линия, то движение называют криволинейным

2. Как определяется декартова прямоугольная система координат?

3. Как определяется абсолютная скорость точки в неподвижной (инерциальной) системе координат? Как направлен вектор скорости по отношению к ее траектории? Чему равны проекции скорости точки на оси декартовых координат?

Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть:

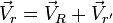
или

.

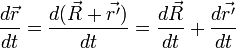3. Как определяется абсолютное ускорение точки в неподвижной (инерциальной) системе координат? Чему равны проекции ускорения точки на оси декартовых координат?

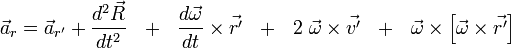
5. Как определяется вектор угловой скорости твердого тела, при его вращении вокруг неподвижной оси? Как направлен вектор угловой скорости?

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

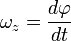а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

6. Как определяется вектор углового ускорения твердого тела, при его вращении вокруг неподвижной оси? Как направлен вектор углового ускорения?

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

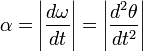
Вектор углового ускорения α направлен вдоль оси вращения (в сторону 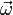при ускоренном вращении и противоположно 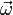— при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть

,

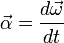8. Чему равны абсолютная, переносная и относительная скорости точки при ее сложном движении?

9. Как определяются переносное и относительное ускорения при сложном движении точки?

10. Как определяется кориолисово ускорение при сложном движении точки?

11. Сформулируйте теорему Кориолиса.

Теорема о сложении ускорений (теорема Кориолиса): , где – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений.

12. При каких движениях точки равны нулю:

а) касательное ускорение?

б) нормальное ускорение?

14. Какое движение тела называется поступательным? Чему равны скорости и ускорения точек тела при таком движении?

16. Какое движение тела называется вращательным? Чему равны скорости и ускорения точек тела при таком движении?

17. Как выражаются касательное и центростремительное ускорения точки твердого тела, вращающегося вокруг неподвижной оси?

18. Каково геометрическое место точек твердого тела, вращающегося вокруг неподвижной оси, скорости которых в данный момент имеют одинаковую величину и одинаковое направление?

19. Какое движение тела называется плоскопараллельным? Чему равны скорости и ускорения точек тела при таком движении?

20. Как определяется мгновенный центр скоростей плоской фигуры, движущейся в своей плоскости?

21. Как можно графически найти положение мгновенного центра скоростей, если известны скорости двух точек плоской фигуры?

22. Каковы будут скорости точек плоской фигуры в случае, когда мгновенный центр вращения этой фигуры бесконечно удален?

23. Как связаны между собой проекции скоростей двух точек плоской фигуры на прямую, соединяющую эти точки?

24. Даны две точки (А и В) движущейся плоской фигуры, причем известно, что скорость точки А перпендикулярна к АВ. Как направлена скорость точки В?