Методы устранения мультиколлинеарности.
Средства от мультиколлинеарности
1. Изменить или увеличить выборку
2. Исключить одну из переменных
3. Преобразовать мультиколлинеарные переменные
- использовать нелинейные формы
- использовать агрегаты (линейные комбинации нескольких переменных
- использовать первые разности вместо самих переменных
4. Ничего не делать!
Гетероскедастичность. Последствия гетероскедастичности.
Суть: Одной из ключевых предпосылок МНК является условие постоянства дисперсий случайных отклонений (параграф 5.1, предпосылка 2°): дисперсия случайных отклонений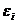 
постоянна. 
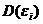= D( 
) = 
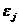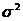для любых наблюдений i и j.
Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностъю (непостоянством дисперсий отклонений).
На рис. 8.1 приведены два примера линейной регрессии — зависимости потребления С от дохода I: С =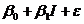 
.
С С
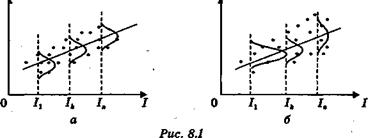
Динамика изменения дисперсий (распределений) отклонений для данного примера проиллюстрирована на рис. 8.2. При гомоскедастичности (рис. 8.2, а) дисперсии 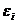постоянны, а при гетероскедастичности (рис. 8.2, б) дисперсии 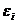изменяются (в нашем примере увеличиваются).
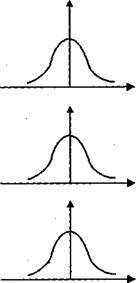Рис 8.2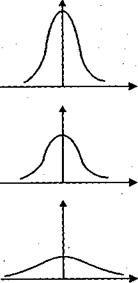 
Проблема гетероскедастичности характерна для перекрестных данных и довольно редко встречается при рассмотрении временных рядов.
Последствия: При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК будут следующими.
Оценки коэффициентов по-прежнему останутся несмещенными и 
линейными.
3. Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут даже асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
4. Дисперсии оценок будут рассчитываться со смещением. Смещенность появляется вследствие того, что не объясненная
уравнением регрессии дисперсия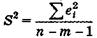 
(т - число объ 
ясняющих переменных), которая используется при вычислении оценок дисперсий всех коэффициентов (формула (6.23)), не является более несмещенной.
4. Вследствие вышесказанного все выводы, получаемые на основе соответствующих t- и F-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, получаемые при стандартных проверках качества оценок, могут быть ошибочными и приводить к неверным за иключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а следовательно, t-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, таковыми на самом деле не являющихся.
Обнаружение:а) Графический анализ остатков
б) Тест ранговой корреляции Спирмена
в) Тест Парка
г) Тест Глейзера
д) Тест Голдфелда—Квандта