Определениие мультиколлинеарности. Признаки наличия мультиколлинеарности.

Мультиколлинеарность (multicollinearity) –положение, при котором одна или более независимых переменных, входящих в уравнение регрессии, являются точными линейными функциями от одной или более других независимых переменных того же уравнения.

Обнаружение мультиколлинеарности

1. Высокий R2 при всех незначимых коэффициентах.

2. Высокие парные коэффициенты корреляции

3. Высокие значения коэффициента VIF

Последствия мультиколлинеарности

1. Оценки коэффициентов остаются несмещенными

2. Стандартные ошибки коэффициентов увеличиваются

3. Вычисленные t-статистики занижены.

4. Оценки становится очень чувствительными к изменению спецификации и изменению отдельных наблюдений.

5. Общее качество уравнения, а также оценки переменных, не связанных мультиколлинеарностью, остаются незатронутыми.

6. Чем ближе мультиколлинеарность к совершенной (строгой), тем серьезнее ее последствия.

29)Методы проверки наличия мультиколлиниарности. Показатель VIF ­– «фактор инфляции вариации»

Мультиколлинеарность - это коррелированность двух или нескольких объясняющих переменных в уравнении регрессии. В результате высококоррелированные объясняющие переменные действуют в одном направлении и имеют недостаточно независимое колебание, чтобы дать возможность модели изолировать влияние каждой переменной.

Для проверки появления мультиколлинеарности применяются 2 метода:

1) вычисление матрицы коэффициентов корреляции для всех объясняющих переменных. Если коэффициенты корреляции между отдельными объясняющими переменными очень велики, то, следовательно, они коллинеарны. Однако, при этом не существует единого правила в соответствии с которым есть некоторое пороговое значение коэффициента корреляции, после которого высокая корреляция может вызвать отрицательный эффект и повлиять на качество регрессии.

2) для измерения эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»:

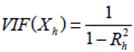- , где 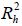- значение коэффициента множественной корреляции, полученное для регрессора 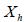, как зависимой переменной и остальных переменных 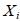. При этом степень мультиколлинеарности, представляемая в регрессии переменной 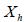, когда переменные 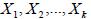включены в регрессию, есть функция множественной корреляции между 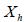и другими переменными .

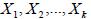­­­­­­ - если 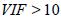, то объясняющие переменные, коррелирующие между собой, считаются мультиколлинеарными.

Существует еще ряд способов, позволяющих обнаружить эффект мультиколлинеарности:

- стандартная ошибка регрессионных коэффициентов близка к нулю;

- мощность коэффициента регрессии отличается от ожидаемого значения;

- знаки коэффициентов регрессии противоположны ожидаемым;

- добавление или удаление наблюдений из модели сильно изменяют значения оценок;

- значение F-критерия существенно, а t-критерия – нет.