Билет 5. Распределение дискретных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение (формулы, пояснения).

Случайная величина – это величина, значение которой может быть различным в зависимости от случайных обстоятельств.

Если случайная величина принимает конечное счетное значение х1, х2,..., которым сопоставляется n значений вероятностей:Р(х1), Р(х2) и т.д., то распределение называется дискретным, а случайную величину – дискретной.

Характеристики случайных величин

Математическое ожидание дискретной случайной величины – это сумма произведений всех возможных её значений на вероятности этих значений.

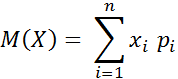
где n – полное число случайных величин.

Дисперсия дискретной случайной величины– это математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

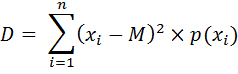
M – математическое ожидание, x_i– случайная величина, р(х_i) – вероятность появления случайной величины

Средним квадратическим отклонением дискретной случайной величины называется квадратный корень из ее дисперсии:

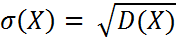
Билет 6. Непрерывные и дискретные случайные величины. Закон распределения Бернулли. Формулы для математического ожидания и дисперсии. Примеры.

Случайная величина – это величина, значение которой может быть различным в зависимости от случайных обстоятельств.

Случайная величина называется дискретной, если она принимает счетное множество значений(число букв на произвольной странице книги, энергия электрона в атоме, число волос на голове человека).

Непрерывная случайная величина принимает любые значения внутри некоторого интервала(температура воздуха за определенный промежуток времени, масса зерен в колосьях пшеницы).

Закон распределения Бернулли

Представим, что в отношении некоторого события А производят n независимых испытаний при условии, что в каждом испытании вероятность (p) появления этого события постоянна. Учитывается два исхода, появление события A и появление противоположного ему события, тоже имеющего постоянную вероятность (q), причем (p+q)=1. При этих условиях, если событиеА появится в nнезависимых испытания m раз, то противоположное ему событие появится (n-m) раз.

Вероятность любого исхода P_n(m), независимо от того, в каком порядке эти события чередуются, выразится произведением p^mq^(n-m), умноженным на биноминальный коэффициент C_n^m:

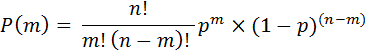
где m – число ожидаемых событий, n – число испытаний, p(m) – вероятность появления соответствующего числа m ожидаемых событий, p – вероятность данного события

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин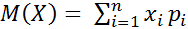

Для непрерывных величин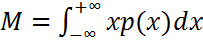

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин

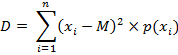
Для непрерывных величин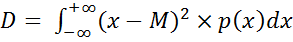

Среднеквадратическое отклонение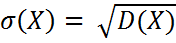

Билет 7. Непрерывные и дискретные случайные величины. Закон распределения Пуассона. Формулы для математического ожидания и дисперсии. Примеры.

Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения. Например, время, масса, объем.

Дискретные величины могут принимать конечное, счетное число случайных значений. Например, год рождения, число людей в автобусе, число страниц в книге.

Распределение Пуассонаприменяется, когда вероятность появления события очень мала и исчисляется сотыми или тысячными долями единицы.

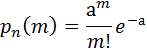
Где m-число ожидаемых событий, P_n(m)-вероятность появления m искомых событий в серии из n независимых испытаний, а-наивероятнейшая частота появления ожидаемого события, е-основание натурального логарифма.