Форсирующее (диференцирующее) звено 1го порядка.

ФЗ 1 порядка – звено дифференциальное уравнение которого имеет вид

X_вых(t)= K[TX_вх(t) + X_вх(t)]

t – постоянная времени характеризующая степень влияния скорости изменения входной величины на выходную.

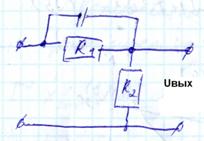Пример: может служить в конце цепочки.

Наличие ФЗ 1 порядка в основном контуре САУ означает введение производной в закон управления что обычно делается в целях улучшения качества управления.

W(p) = k(Tp+1)

Переходная характеристика ФЗ 1 порядка имеет вид:

h(t) = k[Tδ(t) + 1(t)]

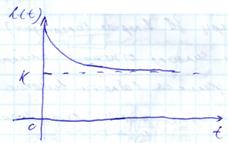
Комплексные переходные характеристики

W(iω) = k(1+iTω)

A(ω) = k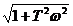

φ(ω) = arctg(Tω)

L(ω) = 20lgk + 20lg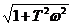

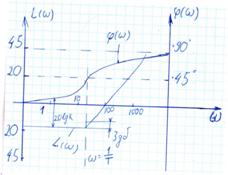Логарифмические частотные характеристики ФЗ 1 порядка обратны соответствующим характеристикам инерционного звена 1 порядка (апериодич.) с увеличением частоты входного сигнала относительная амплитуда выходного сигнала увеличивается в области высоких частот. При изменении частоты входного сигнала от 0 до ∞ сдвиг фазы выходного сигнала относительно входного изменяетя от 0 до 90°.

Форсирующее (диференцирующее) звено 2го порядка.

X_вых(t) = k[T²X_вх(t) + 2Tξ X_вх(t) + 1]

Это произведение нельзя представить как произведение двух двучленов, т.к. в этом случае это звено можно было бы заменить 2мя форсирующими звеньями 1 порядка обьедененных последовательно.

W(p) = k [T²p²+2Tξp + 1]

W(iω) = k [(1-T²ω²) + i2Tξ ω]

A(ω) = k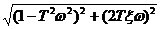

φ(ω) = arctg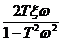

L(ω) = 20lgk + 20lg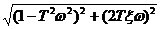

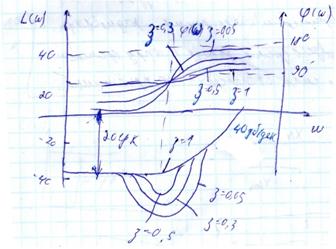
Сравнив формулы фазочастотных характеристик и ЛАЧХ соответствующие формуле колебательного звена мы видим что они отличаются лишь знаком, поэтому L(ω) и φ(ω) форсирующего звена 2 порядка представляет собой зеркальное отражение соответствующих кривых колебательного звена.

Наличие такого звена в таком контуре САУ означает введение 1ой и 2ой производной в закон управления . Это обычно используется для улучшения его качества.

Дифференцирующие звено.

Идеальным ДЗ называется такое звено дифферинцирующего уравнения которое имеет вид:
X_вых = kX_вх(t) (1)

Выходная величина такого звена пропорциональна производной от входной величины.

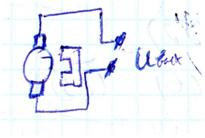
Единственным идеальным дефференцирующем звеном которое в полной мере описывает выражение (1) является тахогенератор постоянного тока.

Если в качестве входной величины рассматривать угол поворота ротора (φ) а в качестве выходной ЭДС якоря (Е). В тахогенераторе постоянного тока при неизменном потоке возбуждения ЭДС в якоре пропорционально скорости вращения.

В режиме близком к холостому ходу, когда сопротивление нагрузки не велико, можно считать что напряжение якоря равно ЭДС.

Е = V

W(iω) = ikω A(ω) = kω φ(ω) = +90° L(ω) = 20lgk + 20kgω

V = k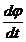

W(p) = kp

h(t) = k*1(t) = kδ(t)

ω(t) = kδ(t) =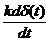

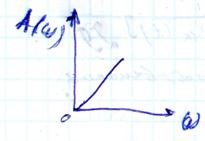
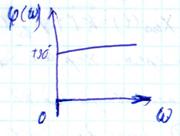
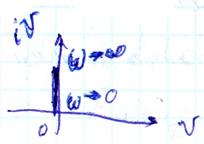
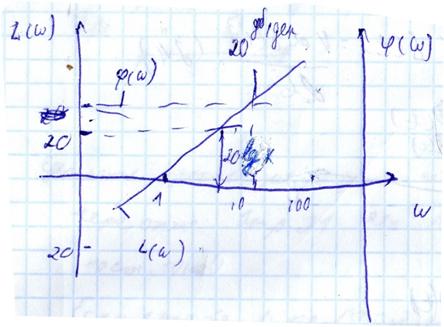
ЛЧХ идеального ДЗ обратны соответствующим характеристикам интегрирующего звена.

Понятие устойчивости САУ.

Определение устойчивостилинейной невозмущенной системы,то есть системы, при нулевом входном сигнале (g(t)º0).

Линейная невозмущенная система:

Линейная система устойчива, если переходный процесс в системе затухает с течением времени, т.е. если собственное (свободное) движение системы

x(t)→0 при t→ .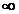

Под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени.

Необходимое условие устойчивости - положительность всех коэффициентов характеристического уравнения. При n³3 оно недостаточно. Как будет показано ниже на ряде примеров САУ третьего порядка (n=3) может оказаться неустойчивой и при положительных коэффициентах дифференциального уравнения.

Если l_i=a_i+w_i - корень характеристического уравнения (i=1..n)

,

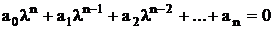то условие устойчивости системы - расположение корней характеристического уравнения в левой полуплоскости комплексного нпременного l (α_i<0).

Это очевидно из равенства

.

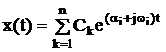(для упрощения предполагается, что у характеристического уравнения нет кратных корней).

21.Переходные и установившиеся процессы.

Переходный процесс:

Переходный процесс характеризуется:

- Длительностью переходного процесса (t _п), то есть временем от начала переходного процесса до момента, начиная с которого выходная величина остается в пределах ±d% от установившегося значения (обычно, d%=±5%).

- Максимальным отклонением регулируемой величины (x_max) или величиной 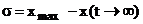) - перерегулированием. Перерегулирование может быть выражено в процентах от установившегося значения )

.

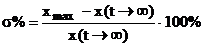Обычно перерегулирование лежит в пределах 10..30%, в некоторых случаях допускается перерегулирование до 70% [2].

- Временем нарастания выходного сигнала (t_н). В точке x(t)=x(t®¥)/2 строят касательную к x(t)и определяют временя нарастания, как показано на рис.1.

- Колебательностью, то есть числом колебаний, которое может наблюдаться в течение времени переходного процесса (обычно, 1..2 колебания, иногда - и 3..4 колебания). В некоторых с системах колебания на допускаются вообще [2].

Используются и другие критерии оценки переходных процессов (например, время запаздывания).

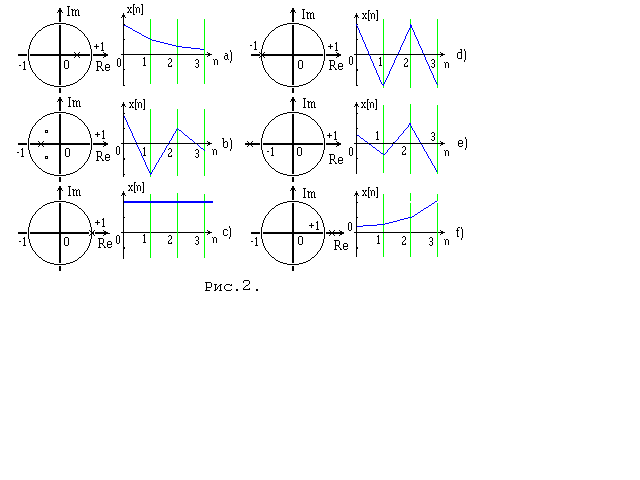Те же критерии оценки применимы и для случая x(t®¥)=0.

Критерий устойчивости САУ.

В ТАУ разработан ряд правил, с помощью которых можно судить о знаках действительных

частей корней, не решая характеристическое уравнение и не находя числовые значения

самих корней. Эти правила получили название критериев устойчивости.

Различают алгебраические и частотные критерии устойчивости.

Алгебраические критерии устанавливают необходимые и достаточные условия

отрицательности корней в форме ограничений, накладываемых на определенные

комбинации коэффициентов характеристического уравнения системы.

Частотные критерии определяют связь между устойчивостью системы и формой ее частотных характеристик.

Понятие об устойчивости системы регулирования связано со способностью. Возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели её из этого состояния. Наглядно устойчивость равновесия можно проил-ть

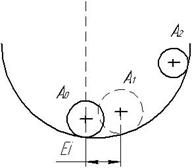В виде шара лежащего в некотором углублении .

При всяком отклонении его от положения равновесия, шар будет стремится вернуться к нему точно ( при отсутствии сил трения)или к некоторой конечной области, окружающ предшеств.равновесия обл-ти

( при наличии сил трения).Такое положение шара будет устойчивым.