Амплитудно-фазовая частотная характеристика.

Дифференциальное уравнение определяет передаточную функцию звена:

.

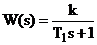Отсюда подстановкой s=jw получаем амплитудно-фазовую частотную характеристику (частотную передаточную функцию) звена

.

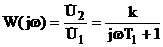Разделим выражение на действительную (U(ω)) и мнимую (V(ω)) части

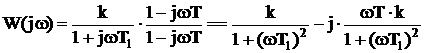
и представим амплитудно-фазовую частотную характеристику как сумму действительной и мнимой частей;

.

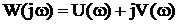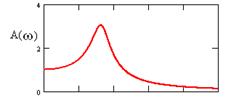
Амплитудная частотная характеристика

.

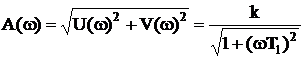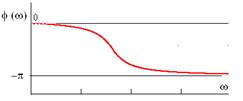
Фазовая частотная характеристика

.

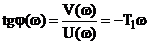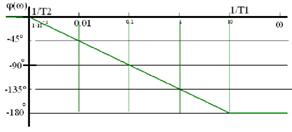
Амплитудная и фазовая частотные характеристики при линейных масштабах по обоим осям :

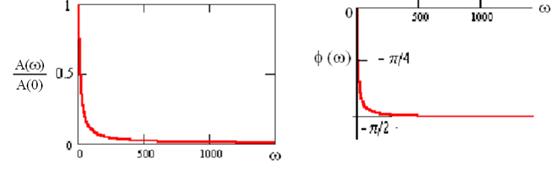
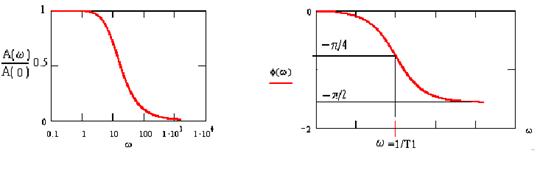
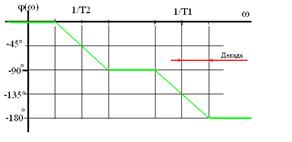
Те же характеристики при логарифмическом масштабе по оси частот и с аппроксимацией асимптотами:

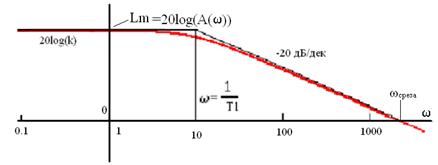
До частоты ω=1/T1 A(ω) ≈20•log(k), а при частотах больших ω=1/T1 (т.н. частоты сопряжения) A(ω) аппроксимируется прямой с наклоном минус 20 дБ на декаду.

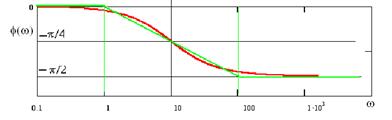
Асимптоты ЛФЧХ - при частоте ω_{сопряжения} фазовый сдвиг минус 45°, отрезок наклонная прямой соединяет точки ± 1 декада от частоты сопряжения.

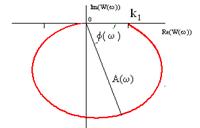
При изменении частоты от w=0 до w=¥ амплитудно-фазовая частотная характеристика (годограф Найквиста)

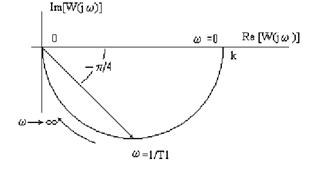
Реакция звена на типовые воздействия:

- единичный скачек ;

- прямоугольный импульс ;

- δ – импульс;

- g(t)=vt

Колебательное звено

Дифференциальное уравнение звена :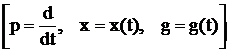

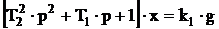
причем T₁<2T₂, так, что корни характеристического уравнения - комплексные.

Тогда уравнение можно переписать уравнение в форме

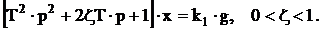
При ζ≥1 звено превращается в т.н. апериодическое звено второго порядка.

Пример колебательного звена – масса на упругом подвесе со слабым скоростным демпфировании (параметр β).

Апериодическое (инерционное) звено второго порядка

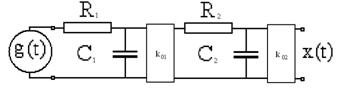
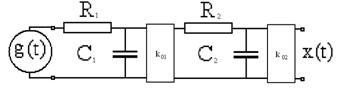
Апериодическое звено второго порядка – это последовательное соединение двух апериодических звеньев через звено, обеспечивающее направленность, в данном случае пропорциональное звено с усилением k₀₁.

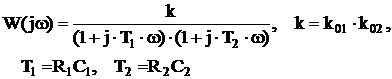
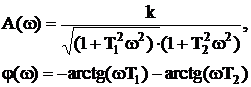
Далее:

ЛАЧХ, ЛФЧХ, реакция на 1(t), δ(t).

Надо отметить, что передаточная функция последовательного соединения типовых звеньев получается простым перемножением их передаточных функций. Имея передаточную функцию последовательного соединения легко записать дифференциальное уравнениеэтого соединения:

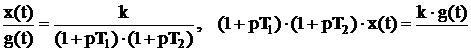
Откуда, после очевидных преобразований и обратной замены 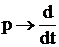, получим

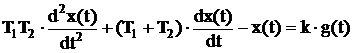
Примечание. Последовательное соединение двух RC- цепочек описывается

другим дифференциальным уравнением и обладает другими динамическими свойствами.

Примеры физических систем со свойствами апериодического звена второго порядка:

- два однозвенных RC-фильтра, разделенных усилителем;

- термопара в металлическом корпусе.

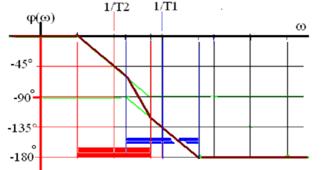
Логарифмическая амплитудная частотная характеристика (красный цвет) и ее аппроксимация асимптотами (черный цвет):

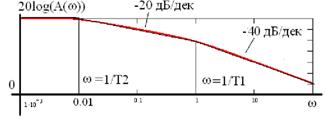
Логарифмическая фазовая частотная характеристика, аппроксимированная асимптотами, для различных значений постоянных времени:

- (1/T11-1/T21)=10⁴ , т.е. четыре декады;

- (1/T1-1/T2)>10⁴ - более четырех декад;

- (1/T1-1/T2)<10⁴ - менее четырех декад;