Формулировка достаточного признака для возможности почленного интегрирования ряда.

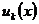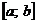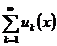Теорема 6:Если все функции непрерывны на сегменте и , то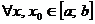

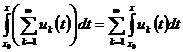, то есть при указанных условиях функциональный ряд можно интегрировать почленно.

· Разложив предварительно производные, путем почленного интегрирования получить разложения в степенной ряд следующих функций: 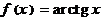. Найдите сумму ряда 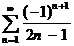(Д 2869).

Теорема 7: Пусть функции 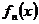имеют непрерывные производные на сегменте 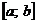Пусть 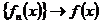хотя бы в одной точке сегмента 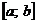, а последовательность производных сходится равномерно на 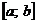.Тогда последовательность 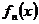сходится равномерно на сегменте к функции 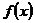, дифференцируемой на сегменте 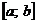и предельная функция 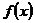имеет производную . Другими словами, последовательность можно дифференцировать почленно.

· Для функциональной последовательности 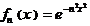, 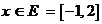(вопрос о равномерной сходимости см. семинар ряды 2 ) а) выяснить вопрос о равномерной сходимости последовательности из производных, б) справедливо или нет равенство ?

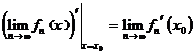· Показать, что последовательность 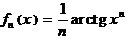сходится равномерно на интервале 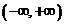, но 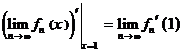(Д2800).

Теорема 8 Если все функции 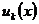имеют производную на сегменте 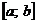и если ряд из производных 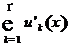сходится равномерно на сегменте к функции 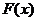, а сам ряд 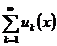сходится хотя бы в одной точке сегмента , то ряд 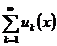сходится равномерно на 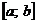к функции 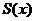, 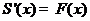. То есть ряд при этих условиях можно дифференцировать почленно.

Показать, что функция 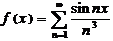непрерывна и имеет непрерывную производную на интервале 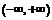(Д2792).

Степенные ряды.

Напомнить определение степенного ряда, формулу Коши-Адамара, определение сходимости и равномерной сходимости, формулы пяти основных разложений в ряд Тейлора.

· Определить радиус и интервал сходимости и исследовать поведение в граничных точках интервала сходимости следующих рядов:

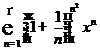(Д 2816),

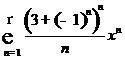(Д 2828).

· Разложить функцию 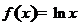в степенной ряд по степеням разности 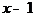и определить интервал сходимости разложения (Д 2840).

· Разложить функцию в степенной ряд а) по степеням x, б) по степеням разности 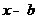, где 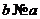в) по степеням и определить интервал сходимости разложения (Д 2839).

· Применяя почленное дифференцирование, вычислите сумму ряда 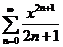(Д 2906),

· Применяя почленное интегрирование, вычислите сумму ряда 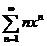( Д 2911).

На дом: ВОС гл.I № 724: Для функциональной последовательности 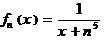, 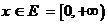установить сходимость, исследовать её на равномерную сходимость и выяснить, справедливо или нет равенство 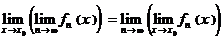при .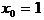

Д2794. Этот пример показывает, что признак возможности предельного перехода достаточный, но не необходимый.

Д 2808.1

Определить область существования функции 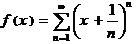и исследовать её на непрерывность.

Д 2804 (этот пример показывает, что признак интегрирования последовательности, лишь достаточный, но не необходимый.)

ВОС гл.I № 744: Для функциональной последовательности 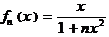, 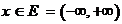а) выяснить вопрос о равномерной сходимости последовательности б) выяснить вопрос о равномерной сходимости последовательности из производных, в) справедливо или нет равенство ?

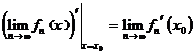Д 2826, 2829, 2858, 2851, 2852, 2853, 2873, 2907, 2912.

На следующем семинаре в качестве контроля - контрольная по домашнему заданию - 3 варианта – задачи 2851, 2852, 2853 (разложение в ряд Маклорена).