Классификация игр. Определение седловой точки.

Классификацию игр можно проводить: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.

В зависимости от количества игроков различают игры двух и  игроков. Первые из них наиболее изучены. Игры трёх и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения. Чем больше игроков - тем больше проблем.

По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной. Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий игра называется бесконечной.

По характеру взаимодействия игры делятся на:

1) бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции;

2) коалиционные (кооперативные)  могут вступать в коалиции.

В кооперативных играх коалиции наперёд определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.

Определение. Если в игре с матрицей А 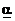= 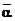(нижняя чистая цена равна верхней чистой цене), то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры u = = .

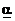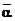Седловая точка  это пара чистых стратегий (_о,_о) соответственно игроков 1 и 2, при которых достигается равенство 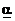= 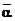.Если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе: 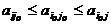, где ,   любые чистые стратегии соответственно игроков 1 и 2; (_о,_о)  стратегии, образующие седловую точку.

Таким образом, седловой элемент 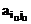является минимальным в _о-й строке и максимальным в _о-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (_о,_о) игроков 1 и 2, образующая седловую точку и седловой элемент 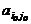, называется решением игры. При этом _о и _о называются оптимальными чистыми стратегиямисоответственно игроков 1 и 2.

Свойства седловых точек:

1. Равноценность. Если в игре несколько седловых точек, то значения функции выигрыша в них одинаковы.

2. Взаимозаменяемость оптимальных стратегий. Игроки могут заменить свои оптимальные стратегии другими оптимальными стратегиями, при этом равновесие не нарушится, а выигрыш (проигрыш) останется неизменным.

13.Определение смешанной стратегии. Решение игры 2*2 в смешанных стратегиях.

Смешанная стратегия это когда вместо того, чтобы применить какую-то одну конкретную стратегию, участники игры могут чередовать (смешивать) в случайном порядке свои стратегии в соответствии со специально разработанной схемой, обеспечивающей нужную частоту, или вероятность реализации каждой из стратегий.

Для каждого игрока можно задать следующие компоненты:

Pia – вероятность применения i-ой стратегии со стороны А.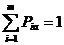

Если подобрать такой набор Pia , который обеспечивает наибольший выигрыш независимо от действий второй стороны, то этот набор вероятностей {p_1a , p_2a , …, p_ma } = S_A и будет называться смешанной стратегией.

S^*_A = {p^*_1a , p^*_2a , …, p^*_ma } – оптимальная смешанная стратегия.

{ S_A } – множество смешанных стратегий со стороны А, из которых нужно выбрать оптимальную.

Игра 2*2 в смешанных стратегиях.

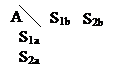
Если хотя бы у одной стороны только 2 действия, применим графо-аналитический метод решения. Зададим игру в виде следующей матрицы:

а11	а12
а21	а22

Для этой игры можно считать следующее: игрок каждый раз играет против какой-либо чистой стратегии другой стороны. При этом он может выбрать такое соотношение вероятностей, которое даст ему гарантированный выигрыш, размером с цену игры.

a₁₁ p^*_1a + a₂₁ p^*_2a = γ - при игре против первой чистой стратегии стороны В.

a₁₂ p^*_1a + a₂₂ p^*_2a = γ – против второй чистой стратегии стороны В.

p^*_1a + p^*_2a = 1

Аналогично для В:

a₁₁ p^*_1b + a₁₂ p^*_2b = γ - при игре против первой чистой стратегии стороны В.

a₂₁ p^*_1b + a₂₂ p^*_2b = γ – против второй чистой стратегии стороны В.

p^*_1b + p^*_2b = 1

Решение системы уравнений:

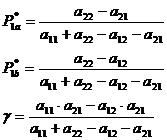
Для того, чтобы полученные решения имели смысл необходимо требовать следующие соотношения:

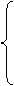
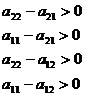или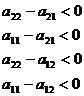

Если выполняется либо одно, либо другое, то вероятности от 0 до 1.

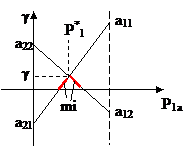
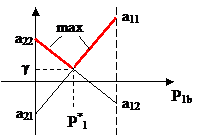
Для стороны А: Для стороны В: