Многопродуктовая статическая модель управления запасами с ограничениями вместимости.

Эта модель предназначена для систем управления запасами, включающие n(>1) видов продукции, которая хранится на одном складе ограниченной площади. Пусть А – максимально допустимая площадь складского помещения для n видов продукции; 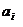- необходимое пространство для хранения единицы iго товара; 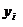- объем заказа iго вида. Ограничение на потребность в складском помещении принимают вид .

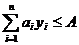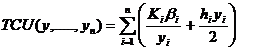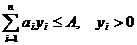
Допустим, что запас продукции каждого вида пополняется мгновенно и скидки цен отсутствуют, дефицит не допускается. Пусть b_i, K_i и h_i – интенсивность спроса, затраты на оформление заказа и затраты на хранение единицы продукции в единицу времени для i-го вида продукции соответственно. Рассматриваемая задача имеет вид: минимизировать при для всех i.

Общее решение этой задачи находится методом множителей Лагранжа. Однако, прежде чем применять этот метод, необходимо установить, действуют ли указанное ограничение, проверив выполнимость ограничений на площадь склада для решения 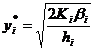неограниченной задачи. Если ограничение выполняется, то оно избыточно, и им можно пренебречь. Ограничение действует, если оно не выполняется для значений 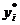. В таком случае нужно найти новое оптимальное значение y_i, удовлетворяющее ограничению на площадь склада в виде равенства. Этот результат достигается построением функции Лагранжа вида 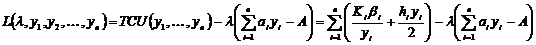, где l(<0) – множитель Лагранжа.

Оптимальные значения y_i и l можно найти, приравняв нулю соответствующие частные производные, что дает , .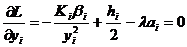

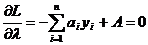Из второго уравнения следует, что значение 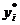должно удовлетворять ограничению на площадь склада в виде равенства. Из первого уравнения следует, что .

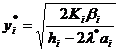Заметим, что 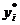зависит от оптимального значения l^* множителя l. Кроме того, при l^*=0 значение 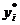является решением задачи без ограничения.

Значение l^* можно найти методом систематических проб и ошибок. Так как по определению в поставленной выше задаче минимизации l<0, то при последовательной проверке отрицательных значений l найденное значение l^* будет одновременно определять значения y^*, которые удовлетворяют заданному ограничению в виде равенства. Таким образом, в результате определения l^* автоматически получаются значения y^* .

9. Динамическая модель управления запасами при отсутствии затрат на
оформление.

Рассматривается задача календарного планирования производства, рассчитанная на n равных периодов. Возможные объемы производства на каждый из периодов ограничены, но могут включать несколько уровней. На протяжении текущего периода могут производится изделия для последующих, но в этом случае необходимо учитывать затраты на хранение.

Основные предположения модели:

1) Отсутствие затрат на оформление заказа

2) Недопустимость дефицита

3) Стоимость производства единицы продукции в любой период либо является постоянной, либо имеет возрастающие предельные затраты, т.е. функция затрат является выпуклой

4) Стоимость хранения единицы продукции в каждый период является постоянной величиной

Предположение об отсутствии дефицита означает, что спрос на продукцию в текущем периоде не может быть удовлетворен за счет ее производства в последнем. Т.е. суммарное производство в текущем периоде должно быть удовлетворено спросу за то же время.

Рассмотрим задачу n-этапного планирования. Можно сформулировать в виде транспортной задачи с kn-пунктами n-пунктами потребления. К – количество возможных уровней производства. Производственные возможности каждого из kn пунктов производства определяют объемы поставок . Объемы потребления определяются объемом спроса для каждого периода.

Себестоимость перевозки от пункта от пункта производства до пунукта назначения определяется суммой затрат используемого производственного процесса и стоимостью хранения единицы продукции.

Оптимальное решение такой транспортной задачи определит объемы производственной продукции для каждого производственного уровня, который минимизирует суммарные затраты на производство и хранение.

10. Модель управления запасами с затратами на оформление заказа.

Основные предположения модели:

1) Дефицит не допускается

2) Затраты на оформление заказа учитываются всякий раз, когда начинается производство новой партии продукции

Существует два метода решения:

1) Точный метод динамического программирования

2)Эвристический прием

Постановка задачи этой модели:

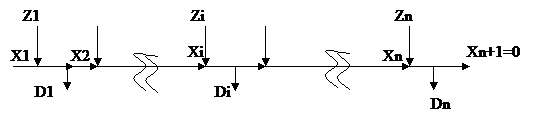Zi – количество заказанной продукции, объем заказа

Di – спрос на продукцию

Xi – объем запаса на начало этапа i.

Стоимостные компоненты:

Ki – затраты на оформление заказа

Hi – затраты на хранение единицы продукции, переходящей из этапа i в i+1.

Ci(Zi) – функция производственных затрат

Ci (Zi) = 0 если Zi=0 и Ci (Zi)= Ki+ Ci (Zi) если Zi>0

Ci (Zi) – функция предельних производственных затрат при заданном значении Zi