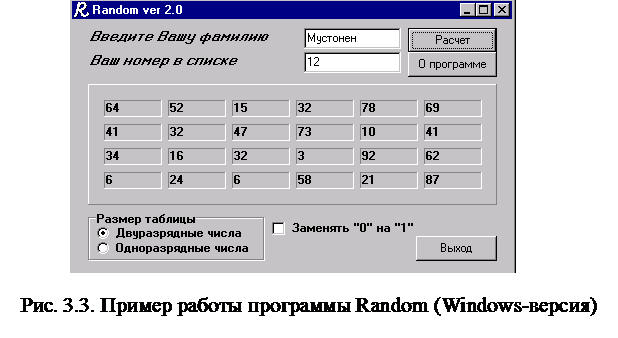
Программа Random (Windows-версия)

Пример: требуется определить выборку по адресу m=n=20, т.е. начиная с ячейки (Ф, 20) в таблице случайных чисел. Определим адреса двухразрядных чисел маски М в соответствии с системой вычетов и перенумерованного алфавита от А до Ф:

№ столбца	№ строки
	По таблице случайных чисел	20	1	2	по таблице случайных чисел	по порядку
	По порядку	20	21	22
	Ф				20	20
	А				1	21
	Б				2	22
	В				3	23

Выборка по маске образует конкретную исходную систему:

			{ai}
{cij}
		0							+ 1
{bj}
		+ 1
								S ai =S bj

Следует учитывать, что вместо нулей ставится единица, исходя из физических предпосылок решаемых экономических задач.

В учебной системе процесс формирования множества числовых вариантов может быть реализован программно. Имеются две версии программы Random для операционных систем DOS и Windows.

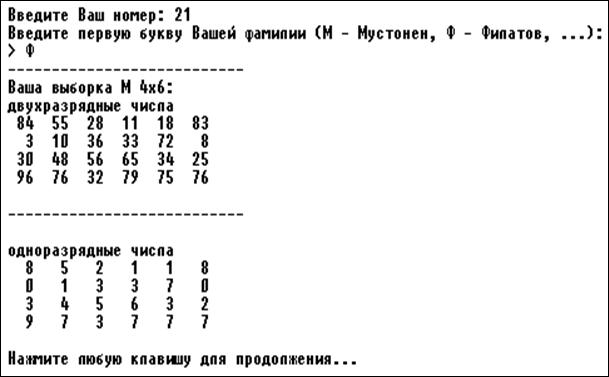
Для DOS-версии программы на экране появится таблица 4х6 (24 числа) из двухразрядных чисел от 00 до 99, а также таблица одноразрядных чисел от 0 или 1 до 9 (рис. 3.2). Для Windows-версии на экране также появятся таблицы одноразрядных и двухразрядных чисел (рис. 3.3).

Числа вписываются в рабочую тетрадь, при этом нули заменяются значащими величинами, например, единицами (для windows-версии существует возможность сразу перевести возникшие нули в единицы).

Для образования из исходной системы I, упорядоченной на случай решения задач ЛП и системы данных D,необходимо выполнить следующие действия:

· составить таблицу транспортной задачи размерности 4´6, в которой 4 источника ресурсов (пунктов отправления) и 6 потребителей (стоков) ресурсов (пунктов назначения);

· заполнить таблицу в соответствии с обозначениями {c_ij}; {a_i}; {b_j} для своего варианта задания. Указанная выборка приведена для варианта (Ф, 20), т.е. получена наложением маски М на транспортную таблицу (см. табл. 3.2).

3.4. Экономическое содержание двойственности

Основа планово-экономических задач: при ограниченных ресурсах достигнуть наилучшего экономического эффекта.

Как правило, любое производство характеризуется готовой продукцией и наличием отходов основного производства. Отходы могут служит сырьем для выпуска вторичных изделий. Возникает двойственная задача оценки отходов с учетом возможности их использования и получения дополнительной прибыли от инвестированных проектов.

Для учебных целей сформируем двойственную пару задач линейного программирования для данной ситуации. Введем знаково-лингвистическое определение ситуации.

Рис. 3.2. Пример работы программы RAND4x6 (DOS-версия)

Виды и количество отходов обозначим через множество Q:

Q={q₁;q₂;…q_j;…q_n},

где q_j – количество q_j для j–го вида отходов.

Виды и количество вторичных изделий обозначим через X:

X={x₁; x₂;…x_i;…x_m},

где {x_i} – неизвестные нам количества, подлежащие планированию.

Стоимость единицы отхода также неизвестна, обозначим ее через y={y₁; y₂;…y_j;…y_n}.

Неизвестная прибыль от прямой продажи отходов может составить .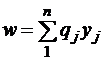

Выбрасывая отходы, мы получаем минимальную прибыль, равную нулю. Желательно увеличить эту прибыль за счет вторичного производства.

Пусть имеются инвестиционные проекты на X видов вторичных изделий или способов использования отходов, по которым известна матрица удельных расходов A=[a_ij] и отходов Q на единицу изделия x_iÎX.

Маркетинг показывает нам рыночную стоимость одного изделия x_iÎX. Пусть она равна b_iÎB:

B={b₁; b₂;…b_i;…b_m}.

С учетом введенных обозначений получаем таблицу типа транспортной.

	Y
X	B	y1		yj		yn
x1	b1	a11		a1j		a1n
xi	bi	ai1		aii		ain
xm	bm	am1		amj
Q	q1		qj		qn

Из последней на алгебраическом уровне абстрагирования формируется следующая двойственная пара задач:

1) суммы по столбцам определяют ОДР – X:

;

–

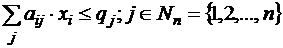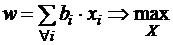задача максимизации прибыли от вторичного использования отходов;

2) суммы по строкам определяют ОДР – Y:

;

–

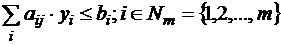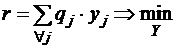задача минимизации расходов покупателя отходов.

Упражнение

Требуется:

1. Составить двойственную пару задач.

Решение:

1.1.

	Y
X	B	y1	y2	y3	y4
x1
x2
Q

1.2.

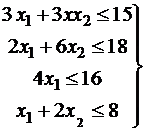ОДР – X

w³20x₁+30x₂®

1.3.

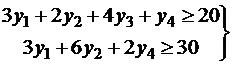ОДР – Y

r£15y₁+18y₂+16y₃+8y₄® .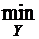

Задание на самостоятельную проработку:

1) Решить задачу п.1.2 графически и алгебраически (путем уточнения координат точек решения). Решение этой задачи рекомендуется проделать самостоятельно.

2) Решить самостоятельно задачу п.1.3, используя табличный алгоритм замены переменных и симплекс-метод.

3) Сравнить результаты решения двойственной пары задач. Проверить выполнение общих свойств двойственности ЗЛП в данном конкретном случае.

4) Дать инвестиционную интерпретацию и составить конкретное описание задачи на знаково-лингвистическом уровне в случае:

(b₁; b₂) – удельная стоимость единичного изделия от реализации проектов (x₁; x₂);

(y₁; y₂; y₃; y₄) – удельная цена составляющих элементов проектов (x₁; x₂);

(q₁; q₂) – объемы инвестиций, предусмотренные на реализацию проектов (x₁; x₂) (активы);

[a_ij] – удельные расходы количеств элементов на реализацию проектов (x₁; x₂);

w – ожидаемая эффективность проекта;

r – эффективность от прямой реализации составляющих проекта;

w=r – условие определения стоимости элементов, определяемая от потребительской стоимости проектов (b₁; b₂) при их реализации в объемах (x₁; x₂).

Транспортная задача (ТЗ)

Линейного программирования

4.1. Составление опорного плана ТЗ