Метода линейного программирования

Математические методы оптимизации относятся к классу
условных экстремальных задач. Внешне эти методы отличаются от постановки обычных задач поиска экстремума функции лишь тем, что здесь экстремум отыскивается при некоторых ограничениях, условиях. Такими ограничениями в этих задачах служат уравнения математической модели системы. Все методы оптимизации можно разделить на две группы: аналитические
и численные.

Для относительно небольшой части инженерных задач, к которым применимы аналитические решения, чаще всего с целью оптимизации применяют метод неопределенных множителей Лагранжа. Сущность метода заключается в использовании функции Лагранжа, позволяющей перевести задачу из класса условных экстремальных задач в класс безусловных (метод поиска экстремума функции).

Большинство задач оптимизации сводятся к численным методам. К таким методам относятся задачи линейного и нелинейного программирования.

К линейному программированию относятся задачи оптимизации, когда как ограничения, налагаемые на параметры, так и выражение для критерия оптимальности являются линейными функциями.

В качестве ограничений можно использовать уравнения математической модели объекта.

Оптимальным значением параметра называеют такое его значение, при котором некоторая вспомогательная функция
(критерий оптимальности) достигает экстремального значения.

Итак, задачи оптимизации — это условные экстремальные задачи, в которых находят экстремум при некоторых ограничениях (условиях).

Задача оптимизации считается задачей линейного программирования, если:

1) критерий оптимальности Р (целевая функция, показатель эффективности) есть линейная функция от параметров х_j:

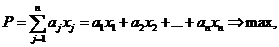(9)

где a_j — заданные коэффициенты.

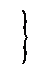2) ограничительные условия, налагаемые на параметры,
имеют вид линейных равенств (или неравенств, которые можно привести к равенствам):

1-е ограничение: a₁₁x₁ + a₁₂x₂ + ... + a_1nx_n = b₁

a₂₁x₁ + a₂₂x₂ + ... + a_2nx_n = b₂ (10)

m-е ограничение: a_m1x₁ + a_m2x₂ + ... + a_mnx_n = b_m.

где n — число параметров,

m - число ограничений.

Эти условия справедливы только в том случае, если

х_j ³ 0. (11)

Уравнение (9) и система уравнений (10) вместе с условием (11) представляют стандартную форму, или основную задачу линейного программирования:

Найти неотрицательные значения параметров х_j (11), которые удовлетворяли бы ограничениям-равенствам (10) и обращали
в максимум функцию (9).

Задача линейного программирования имеет смысл и бес-конечное множество решений только в том случае, когда число неизвестных (число параметров) больше числа ограничений:

(n – m) ,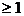

т.е. в оптимизационных задачах число переменных всегда больше числа ограничений.

Задача

Условие

Критерий оптимальности задан в следующем виде:

Р = x₁ + x₂ Þ max.

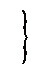Ограничительные условия, налагаемые на параметры, заданы неравенствами:

0,2 х₁ + 0,1 х₂ £ 0,1

(12)

0,1 х₁ + 0,2 х₂ £ 0,1.

Найти, при каких оптимальных значениях параметров х₁ и х₂ критерий оптимальности Р будет максимальным.

Решение

Переведем исходные неравенства в равенства. Для этого необходимо ввести дополнительные переменные х₃ и х₄.

В результате получим систему уравнений 1*, 2* с числом уравнений (ограничений) m = 2 и числом неизвестных параметров n = 4, при условии, х_j :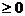

0,2 х₁ + 0,1 х₂ + х₃ = 0,1 (1*)

(13)

0,1 х₁ + 0,2 х₂ + х₄ = 0,1. (2*)

Эту задачу линейного программирования можно решать аналитическим или графическим способом.

Графическое решение задачи

На фазовой плоскости переменных х₁, х₂ представим
область допустимых решений (ОДР) основной задачи линейного программирования, ограниченную условиями (12), или, что то же самое, (13) — при х₃ = х₄ = 0, х_j ≥ 0.

Запишем систему уравнений (13) в более удобном виде:

2 х₁ + х₂ +10 х₃ = 1 (1*)

х₁ +2 х₂ + 10 х₄ = 1. (2*)

Построим прямые, соответствующие этим уравнениям:

1) Из (1*) имеем: х₃ = 0; 2х₁ + х₂ = 1; х₂ = 1 – 2х₁.

Координаты точек для построения прямой: х₂ = 0, х₁ = 0,5
и х₁ = 0, х₂ = 1.

2) Из (2*): х₄ = 0; х₁ + 2х₂ = 1; х₁ = 1 – 2х₂.

Координаты точек для построения прямой: х₁ = 0, х₂ = 0,5
и х₂ = 0, х₁ = 1.

Проведем прямые и обозначим вершины четырехугольника: А, B, C, D.

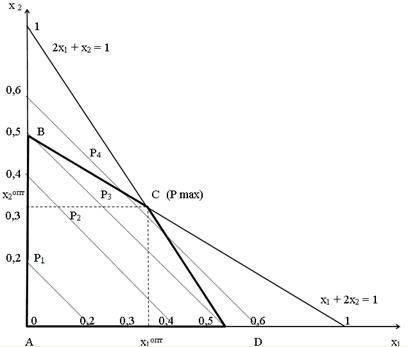
Рис. 1. Графическое решение задачи

3) Далее необходимо рассмотреть целевую функцию:

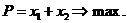
Имеем: х₁ = Р – х₂.

4)В пределах ОДР проведем линию, отвечающую произвольно выбранному значению функции. Допустим, Р₁ = 0,2. Эта линия называется изолинией, линией постоянства критерия оптимальности.

Координаты точек: х₂ = 0, х₁ = 0,2; х₁= 0, х₂ = 0,2.

5)Зададим Р₂ = 0,4 и построим следующую изолинию.

6)Зададим Р₃ = 0,5 и построим третью изолинию.

Очевидно, что целевая функция возрастает и, если передвигать изолинии дальше, мы увидим: одна из этих изолиний (Р₄) пройдёт через вершину С В этой точке и будет максимальное значение целевой функции: х₁ = 1/3 = 0,333, x₂ = 1/3 = 0,333

Рис. 1. Графическое решение задачи

Область ABCD, в которой находятся неотрицательные значения параметров, и будет областью допустимых решений (ОДР) (рис. 1).

3) Далее необходимо рассмотреть целевую функцию

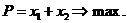
Выразим: х₁ = Р – х₂.

4) В пределах ОДР проведем линию, соответствующую произвольно выбранному значению функции. Допустим, Р₁ = 0,2. Эта линия называется изолинией, линией постоянства критерия оптимальности.

Координаты точек: х₂ = 0, х₁ = 0,2; х₁= 0, х₂ = 0,2.

5) Зададим Р₂ = 0,4 и построим следующую изолинию.

6) Зададим Р₃ = 0,5 и построим третью изолинию.

Очевидно, что целевая функция возрастает и если передвигать изолинии дальше, то одна из этих изолиний (Р₄) пройдёт через вершину С В этой точке и будет максимальное значение целевой функции: х₁ = 1/3 = 0,333, x₂ = 1/3 = 0,333 при Р = 2/3 = 0,666.

Аналитическое решение задачи

Аналитическое решение задачи достигается перебором
базисных решений.

Пусть математическая модель содержит n независимых
линейных уравнений, включающих m параметров (режимных
и конструктивных): x₁, x₂, …, x_m. В задачах оптимизации m > n, а разность k =m – n определяет число свободных (варьируемых) параметров. Если из числа m зафиксировать любые k параметров, принятых в качестве свободных, то систему уравнений можно разрешить однозначно. Решения, где свободные переменные приравниваются нулю, а другие переменные из m параметров принимают неотрицательные значения, называются
базисными решениями. Решение задачи линейного программирования лежит в базисной области.

Исходная система уравнений имеет ограниченное множество базисных решений. Например, в нашем случае при n= 4, m = 2 и k = 4 – 2 = 2 существуют следующие шесть базисных решений: х₁=0, х₂=0; х₁=0, х₃=0; х₁=0, х₄=0; х₂=0, х₃=0; х₂=0, х₄=0; х₃=0, х₄=0.

Доказано, что оптимальное решение в задачах линейного программирования следует искать среди базисных решений.

Поиск проводят перебором всех базисных решений для
выбора из всех параметров х одного параметра — с экстремальным значением критерия оптимальности.

Таблица 2

Свободные переменные	Базисные переменные	ПЭ P = x1 + x2
x1 = 0	x2 = 0	x3 = 1/10	x4 = 1/10	Р = 0
x1 = 0	x3 = 0	x2 = 1	x4 = 1/10	Р = 1
x1 = 0	x4 = 0	x2 = 1/2	x3 = 1/20	Р = 1/2
x2 = 0	x3 = 0	x1 = 1/2	x4 = 1/20	F = 1/2
x2 = 0	x4 = 0	x1 = 1	x3 = –1/10	Р = 1
x3 = 0	x4 = 0	x1 = 1/3	x2 = 1/3	Р = 2/3

Библиографический список

1. Кузнецов Ю.Н., Кузубов В.И., Валощенко А.Б. Математическое программирование. — М.: Высшая школа, 1976. 352с.

2. Ларин Р. М., Плясунов А. В., Пяткин А. В. Методы опти мизации. Примеры и задачи. —Учебное пособие. Новосибирск: Новосибирский государственный университет, 2003. 120 с.

Варианты заданий

В 1

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 4

5х₁+ 4х₂ £ 80

х₁ + 2х₂ £ 32

В 2

Целевая функция Р= 3х₁ + 10х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 6

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 16

В 3

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ + 2х₂ £ 16

10х₁+ 7х₂ £ 70

х₁ – 2х₂ £ 4

В 4

Целевая функция Р= 2х₁ + 9х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 8

10х₁+ 7х₂ £ 70

х₁ + 3х₂ £ 24

В 5

Целевая функция Р= х₁ + 9х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 10

5х₁+ 4х₂ £ 80

х₁ + 2,3х₂ £ 32

В 6

Целевая функция Р= 7х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 4

5х₁+ 4х₂ £ 40

10х₁ + 5х₂ £ 65

В 7

Целевая функция Р= 4х₁ + 9х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 6

10х₁+ 9х₂ £ 90

х₁ + 2х₂ £ 16

В 8

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

х₁ – 2х₂ < 4

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 10

В 9

Целевая функция Р= х₁ + 9х₂ Þ max

Ограничительные условия

10х₁ + 2х₂ £ 70

2х₁ – х₂ > 8

х₁ + 3х₂ £ 24

В 10

Целевая функция Р= 10х₁ + 3х₂ Þ max

Ограничительные условия

5х₁ + 4х₂ £ 48

2х₁ – х₂ < 10

х₁ + 3х₂ £ 30

В 11

Целевая функция Р= 3х₁ + 7х₂ Þ max

Ограничительные условии

х₁ – х₂ £ 4

5х₁+ 4х₂ £ 80

х₁ + 1,5х₂ £ 21

В 12

Целевая функция Р= 10х₁ + 4х₂ Þ max

Ограничительные условия

10х₁ + 7х₂ £ 70

х₁ – 2х₂ £ 4

х₁ + 2х₂ £ 16

В 13

Целевая функция Р= 4х₁ + 9х₂ Þ max

Ограничительные условия

10х₁ + 7х₂ £ 70

х₁ – 2х₂ £ 4

х₁ + 2х₂ £ 16

В 14

Целевая функция Р= 4х₁ + 8,5х₂ Þ max

Ограничительные условия

х₁ + 4х₂ £ 14

3х₁+ 4х₂ £ 18

6х₁ + 2х₂ £ 27

В 15

Целевая функция Р= х₁ + 8х₂ Þ max

Ограничительные условия

2х₁ – х₂ £ 10

5х₁+ 4х₂ £ 80

х₁ + 2х₂ £ 30

В 16

Целевая функция Р= 2х₁ + 9х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 4

5х₁ + 4х₂ £ 60

х₁ + 1,5х₂ £ 21

В 17

Целевая функция Р= 3х₁ + 10х₂ Þ max

Ограничительные условия

2х₁ – 2х₂ £ 6

10х₁+ 2х₂ £ 70

х₁ + 4х₂ £ 45

В 18

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ – 2х₂ £ 4

10х₁+ 7х₂ £ 70

х₁ + 2х₂ £ 10

В 19

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ +2х₂ £ 32

10х₁+ 4х₂ £ 80

х₁ – 23х₂ £ 4

В 20

Целевая функция Р= 3х₁ + 5х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 3

х₁+ х₂ £ 10

3х₁ +9х₂ £75

В 21

Целевая функция Р= 5х₁ + 4х₂ Þ max

Ограничительные условия

х₁ +2х₂ £ 28

10х₁+ 2х₂ £ 52

3х₁ – 2х₂ £ 4

В 22

Целевая функция Р= 3х₁ + 7х₂ Þ max

Ограничительные условия

х₁ – х₂ £ 10

5х₁+ 4х₂ £ 90

х₁ + 2х₂ £ 40

В 23

Целевая функция Р= 10х₁ + 3х₂ Þ max

Ограничительные условия

4х₁ + 3х₂ £ 30

2х₁ – х₂ £ 10

х₁ + 4х₂ £ 24

В 24

Целевая функция Р= 5х₁ + 7х₂ Þ max

Ограничительные условия

4х₁ + 3х₂ £ 30

2х₁ – х₂ £ 8

х₁ + 4х₂ £ 24

В 25

Целевая функция Р= 8х₁ + 3х₂ Þ max

Ограничительные условия

6х₁ – 3х₂ £ 4

6х₁ + х₂ £ 40

х₁ + 2х₂ £ 40