Чему равно расчетное сопротивление древесины пихты 2 сорта при сжатии вдоль волокон?

R_с= R_с * m_п. m_п=0,8

В зависимости от геометрических характеристик R_c=10.4 МПа, 11,2 МПа, 12 МПа, 12,8 МПа.

(табл. 3 и табл. 5. СП)

(П. 3.1. Снип ДК)

Чему равно расчетное сопротивление древесины дуба 2 сорта при сжатии вдоль волокон?

R_с= R_с * m_п. m_п=1,3

В зависимости от геометрических характеристик R_c=16.9 МПа, 18,2 МПа, 19,5 МПа, 20,8 МПа.

(табл. 3 и табл. 5. СП)

(П. 3.1. Снип ДК)

Приведите обозначение и численной значение модуля упругости древесины сосны вдоль волокон?

E₀=10 000 МПа.

(табл. 13 СП)

(П. 3.4. Снип ДК)

Приведите обозначение и численной значение модуля упругости древесины сосны поперек волокон?

E₉₀=400 МПа.

(табл. 13 СП)

(П. 3.4. Снип ДК)

Приведите обозначение и численное значение модуля упругости древесины березы вдоль волокон?

E₀=10 000 МПа.

(табл. 13 СП)

(П. 3.4. Снип ДК)

По какой формуле определяется расчетная длина сжатого элемента?

l_о = lm₀

(табл. 6.5 СП)

(пп. 4.21 и 6.25 Снип ДК)

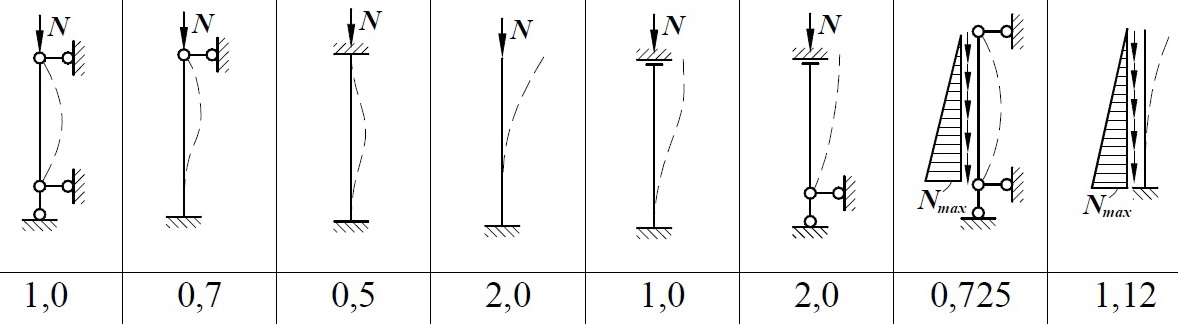
[1.2]11. Приведите схему закрепления концов стержня μ=2,2.

При одном защемленном и другом свободном конце.

(пп. 6.23 СП)

(пп. 4.21 Снип ДК)

[1.2] 12. Приведите схему закрепления концов стержня μ=1,0.

При шарнирно-закрепленных концах, а также при шарнирном закреплении в промежуточных точках элемент.

(пп. 6.23 СП)

(пп. 4.21 Снип ДК)

[1.2] 13. Приведите значение коэффициента А для древесины, используемого при расчете на устойчивость при сжатии.

Коэффициент А = 3000 для древесины

(п.п. 6.3 СП)

[4.3 СНиП ДК]

[1.2] 14. В каких пределах изменяется коэффициент продольного изгиба φ деревянного элемента при значениях гибкости от 0 до 200?

при гибкости элемента l £ 70 от 1 до 0,608;

при гибкости элемента l > 70 от 0,61 до 0,075.

(п.п. 6.3 СП)

[4.3 СНиП ДК]

15. Чему равняется коэффициент а для древесины и фанеры, используемой при расчете на устойчивость при центральном сжатии элемента?

а = 0,8 для древесины и а = 1 для фанеры. [4.3 СНиП ДК]

[1.2] 16. Чему равна Fрасч поперечного сечения центрально-сжатого цельного элемента при симметричном ослаблении, равном 20% F_6p?

Если площадь ослаблений не превышает 25% F_бр, F_расч = F_бр [4.2 СНиП ДК]

[1.2] 17. В каком случае для сжатого элемента Fрасч= F_НТ?

F_рас – расчетная площадь поперечного сечения элемента, F_бр – площадь сечения брутто;

при симметричных ослаблениях, выходящих на кромки, F_рас = F_нт [4.2 СНиП ДК]

[1.2] 18. В каком случае для сжатого элемента Fрасч= 4/3 F_нт?

F_рас – расчетная площадь поперечного сечения элемента, F_бр – площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25% F_бр, F_рас = 4/3 F_нт; [4.2 СНиП ДК]

Выходной контроль

1. Приведите формулу расчета на прочность при центральном сжатии деревянного элемента.

а) на прочность N/ F_нт ≤R_C;

где N – расчетная продольная сила;

F_нт – площадь поперечного сечения элемента нетто. [4.2 СНиП ДК]

2. Приведите формулу расчета на устойчивость при центральном сжатии деревянного элемента.

N/(φ* F_расч) ≤R_C

где R_с – расчетное сопротивление древесины сжатию вдоль волокон;

j – коэффициент продольного изгиба, определяемый согласно п. 4.3;

F_нт – площадь нетто поперечного сечения элемента;

F_рас – расчетная площадь поперечного сечения элемента, [4.2 СНиП ДК]

3. Как вы понимаете выражение «потеря устойчивости» стержня при центральном сжатии?

Происходит при достижении в элементе конструкции сжимающей силой своего критического значения (достаточно дать малейший толчок в поперечном к продольной оси направлении, чтобы стержень потерял устойчивость).

4. Приведите формулу для определения коэффициента φ в упругой области работы древесины.

Коэффициент продольного изгиба j следует определять по формулам:

при гибкости элемента l £ 70: λ=1-а(λ/100)²;

при гибкости элемента l > 70: φ=А/λ²,

где коэффициент а = 0,8 для древесины и а = 1 для фанеры;

коэффициент А = 3000 для древесины и А = 2500 для фанеры. [4.3 СНиП ДК]

5. Приведите формулу для определения коэффициента φ за пределами области упругой работы.

Коэффициент продольного изгиба j следует определять по формулам:

при гибкости элемента l £ 70: λ=1-а(λ/100)²;

при гибкости элемента l > 70: φ=А/λ²,

где коэффициент а = 0,8 для древесины и а = 1 для фанеры;

коэффициент А = 3000 для древесины и А = 2500 для фанеры. [4.3 СНиП ДК]

6. При каком значении гибкости формула Эйлера выходит за пределы пропорциональности?

Если гибкость стержня меньше предельного значения λ<λ_пред, то формула Эйлера становится неприменимой, так как критические напряжения превышают предел пропорциональности и закон Гука неприменим. Формула Эйлера P_кр=(π²EJ)l²

7. Приведите значение предельной гибкости брусчатой колонны.

Сжатые пояса, опорные раскосы и опорные стойки ферм, колонны: lмакс=120 [4.22 СНиП ДК]

8. Приведите значение предельной гибкости сжатых раскосов фермы.

Сжатые пояса, опорные раскосы и опорные стойки ферм, колонны: lмакс=120

Прочие сжатые элементы ферм и других сквозных конструкций: lмакс=150 [4.22 СНиП ДК]

9. Определите значение R_c при следующих условиях?: А2; пихта 2 сорта; элемент подвергнут глубокой пропитке антипиреном под давлением.

Т.к. не указаны напряженное состояние и характеристика элемента принимаем условно: г) элементы из круглых лесоматериалов без врезок в расчетном сечении.

R_c = 16 МПа = 160 кг/см² - для 2 сорта

Расчетные сопротивления для других пород древесины устанавливаются путем умножения величин, приведенных в табл. 3, на переходные коэффициенты m_п, указанные в табл. 4.

R_c = R_c*m_п=16*0,8=12,8 МПа – для пихты.

Расчетные сопротивления, приведенные в табл. 3, следует умножать на коэффициенты условий работы:

R_c = R_c*m_в =12,8*1=12,8 МПа - для А2.

Расчетные сопротивления, приведенные в табл. 3, следует умножать на коэффициенты условий работы

R_c = R_c*m_а =12,8*0,9=11,52 МПа - для элементов, подвергнутых глубокой пропитке антипиренами под давлением.

Ответ: R_c = 11,52 МПа = 115,2 кг/см².

10. Определите значение R_C при следующих условиях эксплуатации: группа A3, температура +40°С; материал элемента - береза, сорт 3.

Характеристика элементов не оговорена, принимаем условно: элементы из круглых лесоматериалов без врезок в расчетном сечении.

R_C= 10 МПа = 100 кгс/см² – для сорта 3;

R_C = R_C *m_п= 10*1,1=11 МПа=110 кгс/см² – для березы;

R_C = R_C *m_в=11*0,9=9,9 МПа= 99 кгс/см² - условия эксплуатации АЗ;

R_C = R_C *m_т = 9,9*0,667= 6,6 МПа =66 кгс/см² - температура +40°С;

Ответ: R_C = 6,6 МПа =66 кгс/см².

11. Определите значение R_C при следующих условиях эксплуатации: группа A3, температура t=20°C; сосна 1 сорта.

Характеристика элементов не оговорена, принимаем условно: элементы прямоугольного сечения высотой до 50 см.

R_C= 14 МПа = 140 кгс/см2 – для сорта 1;

R_C = R_C *m_п= 14*0,65=9,1 МПа=91 кгс/см² – сосна веймутова;

R_C = R_C *m_в=9,1*0,9=8,19 МПа= 81,9 кгс/см² - условия эксплуатации АЗ;

R_C = R_C *m_т = 8,19*1= 8,19 МПа =81,9 кгс/см² - температура +20°С< 35°С;

Ответ: R_C = 8,19 МПа = 81,9 кгс/см².

12. Определите значение R_C при следующих условиях эксплуатации: группа A3, температура t=15°C, В1, лиственница 2 сорта, имеется ветровая нагрузка.

Характеристика элементов не оговорена, принимаем условно: элементы прямоугольного сечения высотой до 50 см.

R_C= 13 МПа = 130 кгс/см2 – для сорта 2;

R_C = R_C *m_п= 13*1,2=15,6 МПа=156 кгс/см² – лиственница;

R_C = R_C *m_в=15,6*0,9=14,04 МПа= 140,4 кгс/см² - условия эксплуатации В1;

R_C = R_C *m_т = 14,04*1= 14,04 МПа =140,4 кгс/см² - температура +15°С< 35°С;

R_C = R_C *m_н=14,04*1,2=16,85 МПа =168,5 кгс/см – ветер;

Ответ: R_C = 16,85 МПа = 168,5 кгс/см².

Тема 2.Соединение элементов деревянных конструкций

На нагелях

Входной контроль