Теория малых упругопластических деформаций А.А. Ильюшина. Гипотезы. Определяющие соотношения. Функция пластичности Ильюшина.
Гипотезы:
- в результате пластической деформации изменения объема не происходит
,
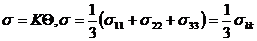а также предполагается что материал несжимаемый
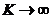
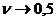
- между интенсивностями напряжений и деформаций существует функциональная связь, которая записывается определенным образом
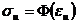
- компоненты тензора напряжений пропорциональны компонентам тензора деформаций (определяющие соотношения – тензорно-линейные)
; 
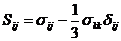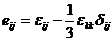
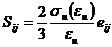
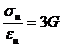
при чистом сдвиге
; 
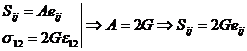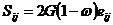
Гипотезы теории малых упругопластических деформаций были подтверждены экспериментально для металлов при простых нагружениях.
Функция пластичности Ильюшина.
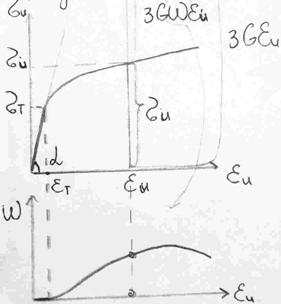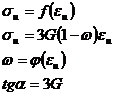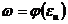 |   - функция пластичности Ильюшина Если задать функцию, модуль сдвига, предел текучести, мы однозначно определим диаграмму деформирования. |
Понятие простого и сложного нагружения. Теорема о простом нагружении.
Простой процесс нагружения – это процесс при котором все компоненты тензора напряжений изменяются пропорционально одному параметру.
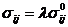
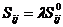
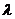- параметр процесса, 
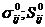- заданные тензоры.
Простому процессу нагружения в пространстве напряжений соответствует траектория в виде прямой линии.
При сложном нагружении направления главных осей и взаимоотношения главных напряжений могут изменяться.
Теорема о простом нагружении.
Для того чтобы во всех точках несжимаемого тела нагруженного внешними силами, изменяющимися пропорционально одному параметру, нагружение было простым, достаточно, чтобы интенсивности напряжений от интенсивности деформаций была степенной функцией.
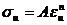
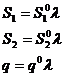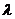 |  - непрерывно возрастающий параметр процесса |  |
Теоремы теории малых упругопластических деформаций А.А. Ильюшина.
- Теорема единственности.
При заданных объемных и поверхностных силах, а также перемещениях на части поверхности, НДС тела определяется единственным образом.
Постановка задачи при упругом нагружении:
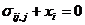
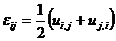
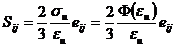
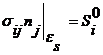
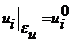
- Теорема о разгрузке.
Перемещения точек (деформации и напряжения) в некоторый момент разгрузки равны разности между их значениями в момент начала разгрузки и перемещениями (деформациями и напряжениями), которые возникли бы в нагруженном теле под действием внешних сил равных разностям нагрузок до и после разгрузки. При этом как нагружение, так и разгрузка должны быть простыми.
 |  |
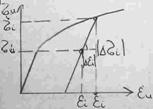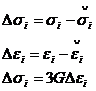Чтобы найти остаточные напряжения, деформации и перемещения необходимо решить упругопластическую и упругую задачи, а затем из одной вы честь другую. Если разгрузка полная, то упругая задача решается при таких же нагрузках, что и упругопластическая
Итерационные методы решения задач теории пластичности. Метод переменных параметров упругости. Метод дополнительных напряжений. Метод дополнительных деформаций.
Постановка задачи.
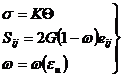- определяющие соотношения при активном нагружении.
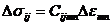
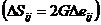- разгрузка
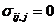- уравнения равновесия
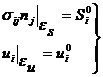- граничные условия
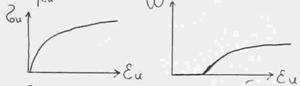
Задача физически нелинейная и решается приближенно с помощью итерационных методов.