Задачи теории пластичности. Диаграммы деформирования материалов. Обратимая и необратимая части деформаций, остаточные напряжения и деформации.

Задачи теории пластичности. Диаграммы деформирования материалов. Обратимая и необратимая части деформаций, остаточные напряжения и деформации.

Задачи теории пластичности.

1. изучение основных закономерностей деформирования твердых тел;

2. постановки и методы решения краевых задач с целью нахождения полей напряжений и деформаций с учетом возникновения пластических деформаций и реологического поведения материала.

Диаграммы деформирования материалов.

Диаграмма деформирования является нелинейной. Она строится на основе экспериментов. Наиболее распространенным видом механических испытаний является одноосное растяжение.

	- длина (рабочая зона) - начальная площадь поперечного сечения
	– усилия – изменение длины ( )

Диаграмма такого рода говорит только о поведении образца, но не материала в целом. Следовательно, необходимо перейти к характеристикам, которые бы отражали поведение материала и не зависели бы от геометрии тела.

- напряжения; - деформация - предел прочности - предел пропорциональности - предел упругости - предел текучести

Точке А диаграммы соответствует напряжение σ и полная деформация ε, которую в свою очередь можно разделить на упругую ε_е и пластическую ε_р. После разгрузки упругая деформация исчезает, а пластическая остается.

Остаточные напряжения и деформации.

Это напряжения и деформации, остающиеся в теле после полной или частичной разгрузки. Остаточные деформации могут состоять из пластических деформаций и упругих. Остаточные напряжения определяются наличием упругой составляющей.

Если в теле было реализовано однородное НДС, то после полного освобождения этого тела от нагрузок, в нем будут присутствовать остаточные деформации (состоящие только из пластической части), а остаточные напряжения будут отсутствовать. Кроме случая с неполной разгрузкой остаточные напряжения возникают также тогда, когда тело не является единым материалом, при наличии концентраторов напряжений и т.д. (т.е. при нарушении однородности поля НДС).

Упругопластическое деформирование начально-анизотропных материалов. Теория Петрищева.

Рассмотрим изотропный и анизотропный материалы при гидростатике:

1. изотропный

1. анизотропный

Теория Петрищева.

- обобщенные интенсивности напряжений и деформаций.

Условные и истинные напряжения и деформации. Условный предел текучести. Эффект Баушингера.

Условные и истинные напряжения и деформации.

	- длина (рабочая зона) - начальная площадь поперечного сечения
	– усилия – изменение длины ( )

такие напряжения и деформации называются условными.

Если , где – значение площади в текущий момент времени, то такие напряжения называются истинными. Если , то такая деформация называется истинной (иногда логарифмической).

Условный предел текучести.

Если материал не имеет четко выраженной площадки текучести, то вводится понятие условного предела текучести .

Условный предел текучести – напряжение, при котором пластическая деформация остающаяся после снятия нагрузки составляет 0,2%.

Эффект Баушингера.

Рассмотрим условный материал, имеющий одинаковые диаграммы растяжения и сжатия.

Осуществим процесс активного нагружения (переход из 1 в 2). Из 2 произведем разгрузку, а затем повторим нагружение. Кривая дойдет до точки 2 и далее опять по диаграмме. В результате предварительной пластической деформации вызванной растяжением предел текучести на растяжение увеличится, а на сжатие – уменьшится. Это явление и носит название эффект Баушингера.

Условия начала пластического течения. Поверхности пластичности в пространстве напряжений. Условие Хубера – Мизеса – Генке. Варианты условий пластичности для анизотропных тел.

Поверхности прочности в пространстве напряжений.

Тензор 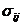- вектор в шестимерном пространстве. Каждая точка в шестимерном пространстве соответствует конкретному напряженному состоянию.

Если осуществляется процесс нагружения, т.е. напряженное состояние непрерывно меняется, то этому процессу будет соответствовать некоторая прямая в пространстве напряжений. Эта линия называется траекторией нагружения.

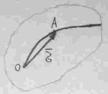Существует некоторая предельная поверхность называющаяся поверхностью текучести. Все точки внутри этой предельной поверхности соответствуют упругому поведению материала. Точки лежащие на предельной поверхности соответствуют моменту перехода в пластическое состояние.

Для того чтобы задать поверхность текучести, нужно задать аналитическое выражение:

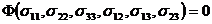- критерий текучести.

Эта функция должна быть задана таким образом, чтобы быть инвариантной по отношению к системе координат:

.

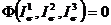Гипотеза единой кривой.

Предполагается, что существует универсальная функциональная зависимость интенсивности напряжений от интенсивности деформаций (графическое выражение – диаграмма деформирования) независящая от вида НДС.

Эксперимент на одноосное растяжение: , остальные Коэффициент Пуассона может меняться, но в пластичности предполагают, что .

Деформационная теория пластичности анизотропных сред Б.Е. Победри. Варианты определяющих соотношений для трансверсально-изотропных и ортотропных материалов. Функции пластичности и их аргументы.

Задачи теории пластичности. Диаграммы деформирования материалов. Обратимая и необратимая части деформаций, остаточные напряжения и деформации.

Задачи теории пластичности.

1. изучение основных закономерностей деформирования твердых тел;

2. постановки и методы решения краевых задач с целью нахождения полей напряжений и деформаций с учетом возникновения пластических деформаций и реологического поведения материала.