Правило Крамера решения систем линейных уравнений.

Габриэль Крамер (1704 – 1752) ─ швейцарский математик, который в 1750 г. нашёл метод решения систем линейных уравнений, названный впоследствии правилом Крамера.

Определение. Система линейных уравнений называется крамеровской,если тело уравнений равно числу неизвестных и определитель матрицы системы отличен от нуля.

Теорема 7.1. Крамеровская система имеет единственное решение, которое находится по формулам

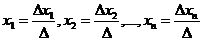
где 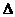─ определитель матрицы системы, 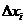─ определитель, полученный из 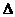, заменой столбца коэффициентов при 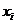на столбец свободных членов.

Доказательство. Пусть дана крамеровская система

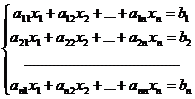(4)

Тогда

│А│= ∆ = 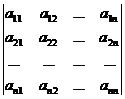¹ 0.

По теореме 3 лекции 6 матрица системы А имеет обратную матрицу А^-1.

Запишем крамеровскую систему (4) в матричном виде

АХ = В (5)

где

А = 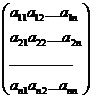, Х = , В = .

Умножим обе части матричного уравнения (5) слева на А^-1:

А^-1(АХ) = А^-1В,

Ввиду ассоциативности умножения матриц имеем

А^-1(АХ) = (А^-1А)Х = Е_ТХ = Х.

Таким образом,

Х = А^-1В ─ решение системы.

1) Покажем, что такое решение единственно. Предположим, что Х₁ и Х₂ ─ два решения матричного уравнения (5). Тогда АХ₁ = В и АХ₂ = В, откуда АХ₁ = АХ₂. Умножая обе чисти равенства на А^-1 слева, имеем

А^-1(АХ₁) = А^-1(АХ₂),

(А^-1А)Х₁ = (А^-1А)Х₂,

Е_nХ₁ = Е_nХ₂,

Х₁ = Х₂.

Следовательно, система (4) имеет единственное решение.

2) Найдём решение системы (4). Из равенства Х = А^-1В имеем:

= ,

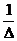
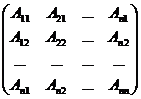
откуда

,

,

……………………………………………………..

.

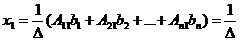
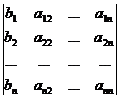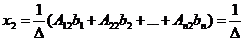
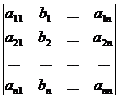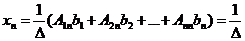
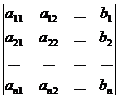Обозначая определители в правой части равенств 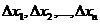соответственно, получим формулы .

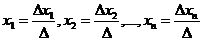Матричный метод решения систем линейных уравнений.

Этот метод также применяется для решения крамеровских систем. Основан он на равенстве

Х = А^-1В,

кторое мы получили при доказательстве теоремы 7.1.

Прямоугольная декартова система координат в пространстве.

Прямоугольная(декартова) система координат в пространствеопределяется заданием масштабной единицы измерения длин и трёх пересекающихся в одной точке О взаимно перпендикулярных осей Ох, Оу и Оz. Точка О называется началом координат,Ох ─ осью ординат,Oz ─ осью аппликат(рис.8.1).

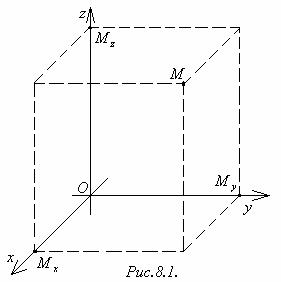Пусть М ─ произвольная точка пространства (рис.8.1). Проведём через точку М три плоскости, перпендикулярные координатным осям. Точки пересечения с осями Ох, Оу и Оz обозначим соответственно М_х, М_у и М_z. Прямоугольными(декартовыми) координатами точки Мв пространстве называются числа х₀, у₀ и z₀, соответствующие точками М_х, М_у и М_z на соответствующих осях. При этом х₀ называется абсциссой, у₀ ─ ординатой, z₀ ─ аппликатой точки М. То, что точка М имеет координаты х₀, у₀ и z₀ обозначается: М(х₀; у₀;z₀).

Плоскости Оху, Оуz и Охz называются координатными плоскостями. Они делят всё пространство на восемь частей, называемых октантами.

Понятие вектора.

Некоторые физические величины (например: температура, масса, объём, длина) могут быть охарактеризованы одним числом, которое выражает отношение этой величины к соответствующей единицы измерения. Такие величины называются скалярными. Другие величины (например: сила, скорость, ускорение) характеризуются не только числом, но и направлением. Эти величины называются векторными. Для описания таких величин в математике введено понятие «вектор».

Определение. Любая упорядоченная пара точек А и В пространства определяет направленный отрезок, т.е. отрезок с заданными на нём направлением. Направленный отрезок называется вектором. На рисунке направление вектора обычно изображают стрелкой. Если в упорядоченной паре точка А первая, то её называют началом вектором, а точку В ─ концом вектора,в этом случае вектор обозначается 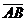. Иногда векторы обозначают малыми буквами , и т.д.

Модулем вектора называется его длина. Обозначают модуль 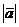или 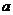. Нуль-вектор (или нулевой вектор) ─ это вектор, начало и конец которого совпадают; обозначается он 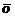. Модуль нуль-вектора равен нулю, а направление не определено. Единичнымназывается вектор, длина которого равна единице.

Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

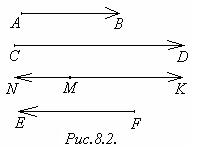
Коллинеарные векторы могут быть направлены одинаково или противоположно (рис.8.2).

Векторы и называются равными(обозначается = ), если они коллинеарны, одинаково направлены и имеют равные модули.

Векторы и называются противоположными(обозначается = − ), если они коллинеарны, противоположно направлены и имеют равные модули.

Три вектора , , называются компланарными,если они лежат в одной плоскости.