Среднеквадратичное приближение функций

Пусть в таблице заданы значения функции, полученные, например, из эксперимента, т. е. измеренные с погрешностью. Тогда приближение с использованием аппарата интерполяции, в основе которого приравнивание значений многочлена в узлах интерполяции табличным значениям, нецелесообразно.

При такой постановке задачи следует выполнить приближение в среднем, т. е. описать таблично заданную функцию некоторой достаточно простой аналитической зависимостью, имеющей небольшое количество параметров. Оптимальный выбор этих параметров и позволит выполнить среднеквадратичное приближение функции, заданной таблицей.

Выбор типа аналитической зависимости следует начинать с нанесения табличных данных на координатную плоскость - так будет сформировано поле экспериментальных точек. Сквозь поле этих точек проводится плавная кривая так, чтобы часть точек легли на эту кривую, часть точек были выше, а часть точек оказались ниже проведённой кривой. По виду этой кривой и следует определить тип аналитической зависимости – линейная ли она, степенная, гиперболическая или какая- либо иная.

Однако по графику на глаз весьма трудно выбрать тип аналитической зависимости. Поэтому был предложен способ ориентировочной оценки и выбора типа аналитической зависимости. Этот способ действительно приблизительный и неточный, так как и кривую можно провести по-разному сквозь поле экспериментальных точек, и в таблице взять разные опорные точки для расчёта да и неизвестна точность предлагаемой методики. Вместе с тем в качестве ориентировочного способа выбора типа зависимости его можно рассмотреть.

Предлагается следующий алгоритм действий.

1. В исходной таблице выбрать две далеко отстоящие друг от друга точки с координатами (x₁,y₁) и (x_n,y_n) - опорные точки, и для каждой пары координат вычислить среднее арифметическое, среднее геометрическое и среднее гармоническое.

2. На кривой, проведённой через поле экспериментальных точек, найти три ординаты, соответствующие найденным абсциссам x_ар,x_геом,x_гарм:

3. Выполнить сравнение найденных на кривой с вычисленными путём вычисления следующих модулей разностей:

4. Из найденных значений 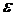выбирается минимальное:

5. Выводы: если минимальным оказалось

- зависимость линейная

- зависимость показательная

- зависимость дробно-линейная

- зависимость логарифмическая

- зависимость степенная

- зависимость гиперболическая

- зависимость дробно-рациональная

Любую из этих зависимостей можно свести к линейной, выполнив преобразование координат или так называемое выравнивание данных. Таким образом, первый этап завершается выбором вида аналитической зависимости, параметры которой не определены.

Второй этап состоит в определении наилучших значений коэффициентов выбранной аналитической зависимости. Для этого применяют математический метод наименьших квадратов.

В основе метода – минимизация суммы квадратов отклонений заданных табличных значений ( ) от вычисленных по теоретической зависимости ( ): .

Пусть выбранная зависимость – прямая линия: . Подставим в функционал : . Тогда минимизируется функционал:

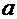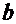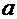Для нахождения наилучших значений коэффициентов и надо найти частные производные от по и 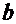и приравнять их нулю:

После преобразований система уравнений приобретает вид:

Решение этой системы линейных уравнений позволяет найти наилучшие значения коэффициентов 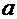и 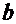линейной зависимости.

Если выбранной зависимостью является квадратичная парабола:

то минимизируется функционал: .

Парабола имеет три варьируемых коэффициента - , наилучшие значения которых следует найти, приравняв нулю частные производные от минимизируемого функционала по искомым коэффициентам . Это позволяет получить следующую систему трёх линейных уравнений для нахождения коэффициентов :

Пример 1. Определить вид зависимости, заданной следующей таблицей.

X
Y	0,55	0,64	0,78	0,85	0,95	0,98	1,06	1,11

Решение.

На координатную плоскость следует нанести заданные в таблице точки – образуется поле экспериментальных данных. Сквозь это поле проводится гладкая кривая.

По таблице выбираются две опорных точки с координатами (3;0,55) и (10;1,11) и для каждой пары абсцисс и ординат вычисляются среднее арифметическое, геометрическое и гармоническое:

Для трёх вычисленных абсцисс по кривой, проведённой через поле экспериментальных точек, определяются три соответствующих ординаты:

Обратить внимание на ориентировочность проводимых вычислений. Далее определяются семь модулей разности:

Получены три минимальных, близких друг к другу значения

На втором этапе следует для каждой из этих зависимостей определить наилучшие значения коэффициентов, применив метод наименьших квадратов, а затем вычислить среднее квадратичное отклонение от заданных табличных значений.

Окончательный выбор аналитической зависимости выполняют по минимальной величине среднего квадратичного отклонения.

Пример 2. В таблице приведены результаты экспериментальных исследований, которые можно аппроксимировать прямой линией. Найти наилучшие значения коэффициентов прямой, применив метод наименьших квадратов.

Решение.

k	Xk	Yk	XkYk	Xk2	Ykтеор	Yk-Ykтеор	(Yk-Ykтеор)2
		66,7			67,50	0,20	0,0400
		71,0	284,0		70,98	0,02	0,0004
		76,3	763,0		76,20	0,10	0,0100
		80,6	1209,0		80,55	0,05	0,0025
		85,7	1799,7		85,77	- 0,07	0,0049
		92,9	2694,1		92,73	0,17	0,0289
		99,4	3578,4		98,82	0,58	0,3364
		113,6	5793,6		111,87	1,73	2,9929
		125,1	8506,8		126,66	- 1,56	2,4336
суммы		811,3	24628,6				5,8496

Общее уравнение прямой: .

Система линейных уравнений, из которой следует определять наилучшие значения коэффициентов 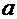и 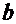, руководствуясь методом наименьших квадратов, имеет вид:

Подставим в систему уравнений вычисленные суммы из 2-го, 3-го, 4-го и 5-го столбцов последней строки таблицы:

Откуда определены коэффициенты линейной зависимости Значит уравнение теоретической прямой имеет вид:

. (*)

В шестом столбце таблицы приведены вычисленные по теоретическому уравнению значений функции для заданных значений аргумента. В седьмом столбце таблицы приведены значения разностей между заданными значениями функции ( 3-ий столбец ) и теоретическими значениями ( 6-ой столбец ), вычисленными по уравнению (*).

В восьмом столбце приведены квадраты отклонений теоретических значений от экспериментальных и определена сумма квадратов отклонений. Теперь можно найти среднее квадратичное отклонение:

Пример 3. Пусть данные эксперимента, приведённые в таблице, аппроксимируются квадратичной параболой: Найти наилучшие значения коэффициентов параболы, применив метод наименьших квадратов.

Решение.

k	Xk	Yk	Xk2	Xk3	Xk4	XkYk	Xk2Yk	Ykтеор	Yk-Ykтеор
		29,8						29,28	0,52	0,2704
		22,9				45,8	91,6	22,22	0,68	0,4624
		17,1				68,4	273,6	17,60	-0,50	0,2500
		15,1				75,5	377,5	15,56	-0,46	0,2116
		10,7				85,6	684,8	11,53	-0,83	0,6889
		10,1				101,0	1010,0	10,60	-0,50	0,2500
		10,6				127,2	1526,4	11,06	-0,46	0,2116
		15,2				228,0	3420,0	14,38	0,82	0,6724
Сум		122,5				731,5	7383,9			3,0173

Система линейных уравнений для определения коэффициентов параболы имеет вид:

Из последней строки таблицы в систему уравнений подставляют соответствующие суммы:

Решение системы уравнений позволяет определить значения коэффициентов:

Итак, заданная таблицей зависимость на отрезке [0;15] аппроксимируется квадратичной параболой:

Расчёт по приведённой формуле для заданных значений аргумента позволяет сформировать девятый столбец таблицы, содержащий теоретические значения функции.

Сумма квадратов отклонений теоретических значений от экспериментальных приведена в последней строке 11-го столбца таблицы. Это позволяет определить среднее квадратичное отклонение:

.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3

Тема: Методы решения систем уравнений

Метод Гаусса - метод последовательного исключения неизвестных – относится к группе точных методов, и если бы отсутствовала погрешность вычислений, можно было бы получить точное решение.

При ручных расчётах вычисления целесообразно вести в таблице, содержащей столбец контроля. Ниже представлен общий вариант такой таблицы для решения системы линейных уравнений 4-го порядка.

				Свободные члены	Столбец контроля

				Свободные члены	Столбец контроля

Пример 1. Методом Гаусса решить систему уравнений 4-го порядка:

Вычисления следует вести в таблице со столбцом контроля, образец которой приведён выше.

				Свободные члены	Столбец контроля
2	-1	-1		-1
		0,5		4,5
	2 -1	-1,5 1,5	-1 -3 -1	3,5 -4 -5,5	-6 -6
		-0,75	-0,5	1,75	1,5
		0,75 0,75	-2,5 -1,5	-5,75 -3,75	-7,5 -4,5
			-3,33	-7,67	-10

Пример 2. Найти корни линейной системы уравнений 3-го порядка:

Составляется аналогичная таблица для определения значений трёх

неизвестных корней системы уравнений.

			Свободные члены	Столбец контроля
-1 -1	-1 -1	-1 -1	11,33	15,33
	-,167	-0,167	1,89	2,56
	5,83 -1,17	-1,17 5,83	33,9 43,9	38,6 48,6
		-0,20	5,80	6,60
		5,60	50,7	56,3
			9,05	10,05

Эти приближённые значения корней можно подставить в исходную систему уравнений и вычислить невязки - , являющиеся разностями между правой и левой частями каждого уравнения системы при подстановке в левую часть найденных корней. Затем подставляются в качестве свободных членов системы невязки и получают поправки

корней - :