Интерполяция по формулам Лагранжа и Ньютона
Интерполяционные многочлены строятся на основе соблюдения условий совпадения значений многочлена в узлах интерполяции с табличными значениями. Степень интерполяционного многочлена на 1 меньше, чем количество узлов интерполяции.
Интерполяционный многочлен Лагранжа используют в таблицах с неравноотстоящими значениями аргумента.
.
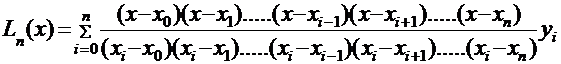Перед вычислениями формулу удобно преобразовать, чтобы вычисления вести в следующей таблице.
| x-x0 | x0-x1 | x0-x2 | x0-x3 | … | … | … | x0-xn | D0 | y0/D0 |
| x1-x0 | x-x1 | X1-x2 | x1-x3 | … | … | … | x1-xn | D1 | y1/D1 |
| x2-x0 | x2-x1 | x-x2 | x2-x3 | … | … | … | x2-xn | D2 | y2/D2 |
| … | … | … | … | … | … | … | … | … | |
| … | … | … | … | … | … | … | … | … | |
| xn-x0 | xn-x1 | xn-x2 | xn-x3 | … | … | … | x-xn | Dn | yn/Dn |
Преобразованная формула принимает вид:
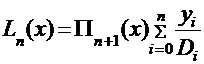. В формуле введены следующие обозначения:
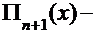произведение элементов главной диагонали таблицы,
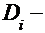произведение элементов i-ой строки таблицы, включая диагональный элемент. Погрешность интерполяции можно оценить по формуле:
.
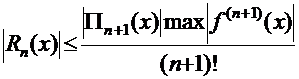Пример 1. Для таблично заданной функции найти значение y при x=0,527 с шестью значащими цифрами после запятой, используя интерполяционный многочлен Лагранжа.
| K | ||||||
| Xk | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | 0,75 |
| Yk | 1,63597 | 1,73234 | 1,87686 | 2,03345 | 2,22846 | 2,83973 |
Составляется таблица разностей.
| Dk 10-6 | Yk/Dk 106 | ||||||
| 0,097 | -0,050 | -0,120 | -0,190 | -0,270 | -0,320 | -9,55411 | -0,171232 |
| 0,050 | 0,047 | -0,070 | -0,140 | -0,220 | -0,270 | 1,36798 | 1,266347 |
| 0,120 | 0,070 | -0,023 | -0,070 | -0,150 | -0,200 | 0,40572 | 4,625998 |
| 0,190 | 0.140 | 0,070 | -0,093 | -0,080 | -0,130 | -1,80093 | -1,129113 |
| 0,270 | 0,220 | 0,150 | 0,080 | -0,173 | -0,050 | 6,18572 | 0,361427 |
| 0,320 | 0,270 | 0,200 | 0,130 | 0,050 | -0,223 | -25,04736 | -0,113374 |
Сумма элементов последнего столбца таблицы разностей:
S = 4,840053 106.
Произведение элементов главной диагонали:
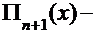0,3762 10-6.
Искомое значение функции при x=0,527 найдено:
Y(x=0,527)=1,82083.
Проверка в системе MathCAD y=1,8208805.
Интерполяционные формулы Ньютона применяют в таблицах с постоянным шагом h=const, причём, 1-ую формулу Ньютона используют для интерполяции в начале таблицы, 2-ую формулу Ньютонаиспользуют для интерполяции в конце таблицы.
В основе формул Ньютона – аппарат конечных разностей.
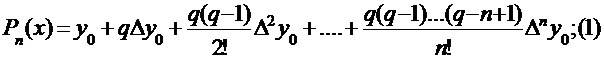
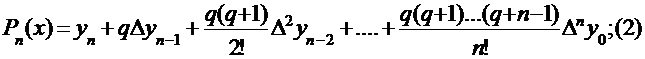
Для расчёта по формулам Ньютона к исходной таблице присоединяют справа таблицу конечных разностей.
| k | xk | yk |  yk | 2yk | 3yk |
| x0 x1 x2 x3 x4 | y0 y1 y2 y3 y4 | y0 y1 y2 y3 | 2y0 2y1 2y2 | 3y0 3y1 |
В 1-ую интерполяционную формулу Ньютона подставляют значения из первой строки таблицы конечных разностей, а значение параметра q вычисляют по формуле: q = (x-x0)/h>0.
Во 2-ую интерполяционную формулу Ньютона подставляют значения с диагонали таблицы конечных разностей, а значение параметра q вычисляют по формуле: q = (x-xn)/h<0.
Степеньинтерполяционного многочлена Ньютона определяется порядком тех конечных разностей, которые оказываются практически постоянными в построенной таблице конечных разностей.
Эти формулы используют и для экстраполяции, точность которой невелика: 1-ую формулу – для интерполяции “вперёд” и экстраполяции “назад”; 2-ую формулу – для интерполяции “назад” и экстраполяции “вперёд”.
Пример 2.
Функция задана таблицей с равноотстоящими значениями аргумента. Найти значения y для x=1,217 и x=1,253.
| xk | yk | yk | 2yk |
| 1,215 1,220 1,225 1,230 1,235 1,240 1,245 1,250 1,255 1,260 | 0,106044 0,106491 0,106935 0,107377 0,107818 0,108257 0,108696 0,109134 0,109571 0,110008 | 0,000447 0,000444 0,000442 0,000441 0,000439 0,000439 0,000438 0,000437 0,000437 | -0,000003 -0,000002 -0,000001 -0,000002 0,000000 -0,000001 -0,000001 0,000000 |
В данном примере конечные разности первого порядка практически постоянны, а это приводит к тому, что конечные разности второго порядка близки к нулю.
Чтобы найти значение функции для аргумента x=1,217, находящегося вблизи начала таблицы, воспользуемся 1-ой формулой Ньютона и вычислим:
q =( 1,217 – 1,215 ) : 0,005 = 0,4
Подставляем в 1-ую формулу значения из первой строки таблицы:
y( x=1,217) = 0,106044 + 0,4 (0,000447) + (0,4 (-0,6): 2)(-0,000003)=
= 0,106044 + 0,000179 + 0,0000003 = 0,106223
Чтобы найти значение функции для аргумента x=1,253, находящегося вблизи конца таблицы, воспользуемся 2-ой формулой Ньютона и вычислим:
q =( 1,253 – 1,260 ) : 0,005 = -1,4
Подставляем во 2-ую формулу значения конечных разностей с диагонали таблицы:
y( x=1,253) = 0,110008 + (-1,4) 0,000437 = 0,110008 - 0,000612 = 0,109396