Деление приближенных чисел (УМНОЖЕНИЕ В 76 ВОПРОСЕ)

Правило 1. Предельная относительная погрешность частного приближенно равна сумме предельных относительных погрешностей делимого и делителя.
Пример 1. Приближенное число 50,0 делится на приближенное число 20,0. Предельная погрешность делимого и делителя 0,05. Тогда предельная относительная погрешность делимого есть

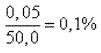
а предельная относительная погрешность делителя есть

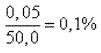
Предельная относительная погрешность частного 50,0:20,0 = 2,50 должна составлять приблизительно
0,1% + 0,25% =0,35%. Действительно, истинная величина частного не больше, чем
(50,0 - 0,05): (20,0+ +0,05) = 2,50877, и не меньше, чем
(50,0 — 0,05): (20,0+0,05) = 2,49127. Если истинное значение частного есть 2,50877, то абсолютная погрешность составляет
2,50877 — 2,50 = 0,00877. Если же истинное значение есть 2,49127, то абсолютная погрешность составит
2,50 — 2,49127 = 0,00873. Рассмотренные случаи — самые неблагоприятные. Значит, предельная относительная погрешность составляет
0,00877:2,50 = 0,00351, т. е. приближенно 0,35%.
Замечание. Точная величина предельной относительной погрешности всегда превышает приближенную, вычисленную по правилу 1. Процент превышения примерно равен предельной относительной погрешности делителя. В нашем примере превышение составляет 0,00001, что составляет 0,29 % от 0,0035. Предельная же относительная погрешность делителя равна 0,25 %. Пример 2. Найти предельную абсолютную погрешность частного 2,81: 0,571. Решение. Предельная относительная погрешность делимого есть
0,005:2,81=0,2%; делителя 0,0005 : 0,571 = 0,1%;
частного 0,20% + 0,10% = 0,3 %. Предельная абсолютная погрешность частного приближенно равна 2,81/0,571 * 0,003 = 0,015. Значит, в частном 2,81 : 0,571 = 4,92 уже третья значащая цифра ненадежна. Более простая, но зато более грубая оценка точности частного основана на подсчете точных цифр. Вот эта оценка:
Правило 2. Пусть делимое и делитель имеют каждое по k значащих цифр. Тогда абсолютная погрешность частного в худшем случае близка к 1,05 единицы (k —1)-го знака (этого значения она никогда не достигает).
Как видим, предельная погрешность частного теоретически вдвое больше предельной погрешности произведения. Однако на самом деле погрешность частного превосходит 5 единиц k-й цифры лишь в исключительных случаях (один раз из тысячи). Поэтому в частном следуеm брать столько же значащих цифр, сколько их имеют делимое и делитель.
Если же одно из данных чисел (делимое или делитель) имеет больше значащих цифр, чем другое, то следует отбросить все лишние цифры или сохранить только первую из них (в качестве запасной).
Если требуется, чтобы частное имело заранее данное число верных цифр, то в делимом и делителе нужно иметь на одну значащую цифру больше.

Возведение в степень приближенных чисел (ЧИСЛА 68 И 42 ЭТО ПРИМЕР. ВМЕСТО НИХ НАДО ПОДСТАВИТЬ ОДИНАКОВОЕ ЧИСЛО.)

Пусть требуется вычислить площадь прямоугольного участка, длина которого 68 м, а ширина — 42 м. Если бы числа 68 и 42 были точные, площадь участка в точности равнялась бы

68 * 42 = 2856 кв. м.

Но числа 68 и 42 не точные, а приближенные: в длине не ровно 68 м, а немного больше или меньше, так как невероятно, чтобы метр укладывался в ней в точности 68 раз. Да и самая длина метровой линейки едва ли в точности была равна 1 м. Мы можем, согласно предыдущему, выразить длину участка в метрах так:

68,?

Подобным же образом и ширину участка выразим через

42,?

Проделаем теперь умножение приближенных чисел:

68,? X 42,?

Выполнение действия видно из следующей схемы:

	Х			,	?
			,	?
			?	?	?
				?
			?
			?,	?	?