Сходящиеся и расходящиеся числовые ряды.
Простейшие свойства сходящихся рядов.
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.
2. Если ряд 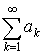 сходится, то
сходится, то 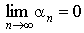 .
.
3. Если ряд 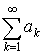 сходится, то сходится ряд
сходится, то сходится ряд 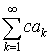 и имеет место равенство
и имеет место равенство 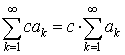 .
.
4. Если ряды 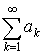 и
и 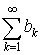 сходятся, то сходится и ряд
сходятся, то сходится и ряд 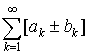 имеет место равенство
имеет место равенство 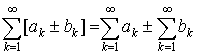 .
.
5. Если ряд 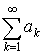 сходится, то
сходится, то 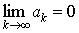 .
.
Отсюда следует
Признак расходимости ряда. Если 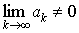 , то ряд
, то ряд 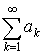 расходится
расходится
Исследование ряда на сходимость.
| Сходимость рядов. Признаки сравнения |
Необходимый признак сходимости, вообще говоря, не гарантирует сходимости ряда. Сходимость или расходимость ряда устанавливается с помощью достаточных признаков. Признаки сравнения, которые мы рассмотрим ниже, как раз и представляют собой достаточные признаки сходимости или расходимости рядов. Признаки сравнения рядов Даны два ряда 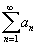 и и 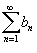 − такие, что − такие, что 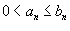 для всех n. Тогда справедливы следующие признаки: Если для всех n. Тогда справедливы следующие признаки: Если 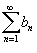 сходится, то сходится, то 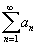 также сходится; Если также сходится; Если 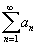 расходится, то расходится, то 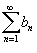 также расходится. Предельные признаки сравнения рядов Пусть даны два ряда также расходится. Предельные признаки сравнения рядов Пусть даны два ряда 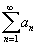 и и 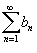 , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: Если , у которых члены an и bn положительны для всех n. Тогда справедливы следующие предельные признаки: Если 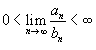 , то оба ряда , то оба ряда 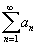 и и 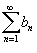 либо сходятся, либо расходятся; Если либо сходятся, либо расходятся; Если 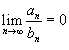 , то ряд , то ряд 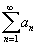 сходится, если сходится ряд сходится, если сходится ряд 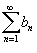 ; Если ; Если 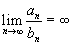 , то ряд , то ряд 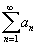 расходится, если расходится ряд расходится, если расходится ряд 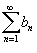 . Так называемый обобщенный гармонический ряд . Так называемый обобщенный гармонический ряд 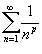 сходится при p > 1 и расходится при 0 < p ≤ 1. сходится при p > 1 и расходится при 0 < p ≤ 1. |
| Пример 1 |
Определить, сходится или расходится ряд 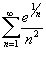 . Решение. Легко видеть, что . Решение. Легко видеть, что 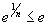 для n > 1. Применяя далее признак сравнения, находим для n > 1. Применяя далее признак сравнения, находим 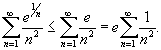 Поскольку ряд Поскольку ряд 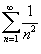 сходится как обобщенный гармонический ряд с показателем степени p = 2, то исходный ряд также сходится. сходится как обобщенный гармонический ряд с показателем степени p = 2, то исходный ряд также сходится. |
Признак Даламбера.
Признак Даламбера — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
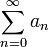
существует такое число 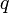 ,
, 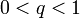 , что начиная с некоторого номера выполняется неравенство
, что начиная с некоторого номера выполняется неравенство
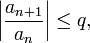
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
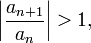
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме
Если существует предел
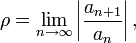
то рассматриваемый ряд абсолютно сходится если 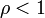 , а если
, а если 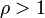 — расходится .
— расходится .
Замечание. Если 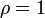 , то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
, то признак д′Аламбера не даёт ответа на вопрос о сходимости ряда.
Примеры
Ряд
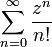
абсолютно сходится для всех комплексных 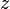 , так как
, так как
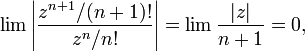
Ряд
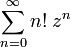
расходится при всех 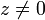 , так как
, так как
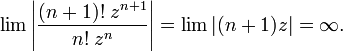
Если 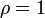 , то ряд может как сходиться, так и расходиться: оба ряда
, то ряд может как сходиться, так и расходиться: оба ряда
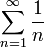 и
и 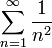
удовлетворяют этому условию, причём первый ряд расходится, а второй сходится.
38. Признак Коши.
Радикальный признак Коши — признак сходимости числового ряда:
Если для числового ряда 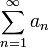 с неотрицательными членами существует такое число с неотрицательными членами существует такое число 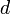 , , 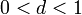 , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство 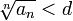 , то данный ряд сходится. , то данный ряд сходится. |
Предельная форма
Условие радикального признака равносильно следующему:
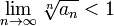
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда 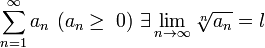 , то если , то если 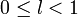 ряд сходится, если ряд сходится, если 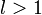 ряд расходится, если ряд расходится, если 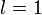 вопрос о сходимости ряда остается открытым. вопрос о сходимости ряда остается открытым. |
Доказательство
1. Пусть 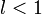 . Очевидно, что существует такое
. Очевидно, что существует такое 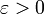 , что
, что 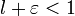 . Поскольку существует предел
. Поскольку существует предел 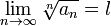 , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
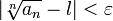
Раскрыв модуль, получаем:
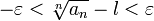
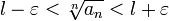
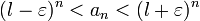
Поскольку 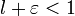 , то ряд
, то ряд 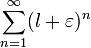 сходится. Следовательно, по признаку сравнения ряд
сходится. Следовательно, по признаку сравнения ряд 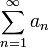 тоже сходится.
тоже сходится.
2. Пусть 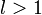 . Очевидно, что существует такое
. Очевидно, что существует такое 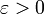 , что
, что 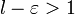 . Поскольку существует предел
. Поскольку существует предел 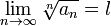 , то подставив в определение предела выбранное
, то подставив в определение предела выбранное  получим:
получим:
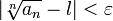
Раскрыв модуль, получаем:
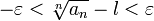
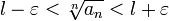
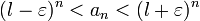
Поскольку 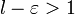 , то ряд
, то ряд 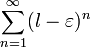 расходится. Следовательно, по признаку сравнения ряд
расходится. Следовательно, по признаку сравнения ряд 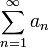 тоже расходится.
тоже расходится.
Примеры
1. Ряд
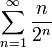
сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
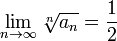
2. Рассмотрим ряд
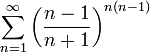
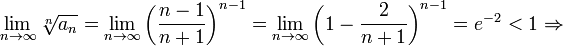 ряд сходится.
ряд сходится.
