ИНЖЕНЕРНО – ТЕХНИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ
61-2016
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к контрольной работе № 1
по математике для студентов
инженерно–технических специальностей
заочной формы обучения
Воронеж 2016
| Составители: | канд. физ.-мат. наук | А.П. Бырдин, |
| канд. физ.-мат. наук | Е.И. Иохвидов, | |
| канд. техн. наук | А.А. Сидоренко, |
канд. физ.-мат. наук М.Ф. Томилов
УДК 517.2 (07)
Методические указания к контрольной работе №1 по математике для студентов инженерно–технических специальностей заочной формы обучения / ФГБОУ ВО “Воронежский государственный технический университет”; cост. А.П. Бырдин, Е.И. Иохвидов, А.А. Сидоренко, М.Ф. Томилов. Воронеж, 2016. 50 с.
Методические указания предназначены для студентов-заочников инженерно–технических специальностей и содержат рекомендации к работе над курсом математики, программу курса с указанием литературы, примеры решения задач и двадцать вариантов контрольных заданий.
Ил. 2. Табл. 1. Библиогр.: 6 назв.
Рецензент канд. физ.-мат. наук, доц. В.И. Кузнецова
Ответственный за выпуск зав. кафедрой д-р техн.
наук, проф. В.И. Ряжских
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
Ó ФГБОУ ВО “Воронежский государственный технический университет”, 2016
ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ
К ИЗУЧЕНИЮ КУРСА МАТЕМАТИКИ
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, включающая его изучение по рекомендованным учебникам, решение задач с помощью учебных пособий, самопроверка и только затем - выполнение контрольных работ. Завершающим этапом изучения отдельных частей курса математики является сдача зачетов и экзаменов в соответствии с учебным планом.
При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, формулы, уравнения и т.д. Курс математики разбит на темы и пункты, в которых указана литература, рекомендуемая для изучения.
Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь. В пособии [6] имеется большое количество решенных задач, с которыми студентам рекомендуется ознакомиться при изучении соответствующего материала.
После изучения определенной темы по учебнику и решения достаточного количества задач рекомендуется воспроизвести по памяти определения, формулы, формулировки теорем. Необходимый минимум вопросов для самопроверки приведен на страницах 6 - 8.
Зачет контрольной работы преподавателем осуществляется при выполнении следующих требований:
· правильном и подробном решении задач в контрольной работе,
· умении достаточно быстро и без помощи пособий решать задачи, аналогичные задачам, предложенным в контрольной работе,
· твердом знании основных формул и определений, перечисленных в вопросах для самопроверки.
Если в процессе изучения теоретического материала или при решении задач у студентов возникают вопросы, справиться с которыми самостоятельно не удается, то за помощью можно обратиться к преподавателю на консультации.
Выбор варианта контрольной работы студентом производится по двум последним цифрам номера студенческого билета в соответствии со следующей таблицей.
| Предпоследняя цифра x совпадает с одной из цифр: 0, 2, 4, 6, 8. | Предпоследняя цифра x совпадает с одной из цифр: 1, 3, 5, 7, 9. |
| x1 – 1–й вариант x2 – 2–й вариант x3 – 3–й вариант x4 – 4–й вариант x5 – 5–й вариант x6 – 6–й вариант x7 – 7–й вариант x8 – 8–й вариант x9 – 9–й вариант x0 – 10–й вариант | x1 – 11–й вариант x2 – 12–й вариант x3 – 13–й вариант x4 – 14–й вариант x5 – 15–й вариант x6 – 16–й вариант x7 – 17–й вариант x8 – 18–й вариант x9 – 19–й вариант x0 – 20–й вариант |
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ требуется строгое соблюдение указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены.
1. Контрольная работа выполняется в тетради в клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля для замечаний рецензента.
2. На обложке контрольной работы должны быть ясно написаны фамилия и инициалы студента, шифр, название дисциплины, номер и вариант контрольной работы, адрес студента. В конце работы ставится дата ее выполнения и подпись.
3. В работу включаются все задачи, указанные в задании, строго по положенному варианту.
4. Решения задач располагаются в порядке возрастания их номеров, указанных в задании, сохраняя номера задач.
5. Условия задач приводятся полностью. Решения излагаются подробно и аккуратно, объясняются все действия по ходу решения и делаются необходимые чертежи.
6. После получения проверенной работы исправляются отмеченные рецензентом ошибки и выполняются все рекомендации рецензента.
ПРОГРАММА КУРСА “ВЫСШАЯ МАТЕМАТИКА”
ДЛЯ СТУДЕНТОВ –- ЗАОЧНИКОВ
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
К КОНТРОЛЬНОЙ РАБОТЕ №1
1. Что называется определителем? Каковы свойства определителей и методы их вычисления? Что такое минор и алгебраическое дополнение?
2. Запишите в общем виде систему линейных уравнений. Какая система называется однородной, неоднородной? Напишите формулы Крамера. Когда применимы эти формулы?
3. Дайте определение геометрическим векторам, сложению и вычитанию векторов. Как определяются скалярное, векторное и смешанное произведения векторов? Как эти произведения выражаются через координаты векторов?
4. Напишите следующие уравнения плоскости: общее уравнение, нормальное уравнение, уравнение плоскости, проходящей через данную точку с заданной нормалью, уравнение плоскости в отрезках. Каковы условия параллельности и перпендикулярности плоскостей?
5. Напишите общие уравнения прямой в пространстве, канонические уравнения, уравнения прямой, проходящей через две точки. Каковы условия параллельности и перпендикулярности прямых? Запишите условия параллельности и перпендикулярности прямой и плоскости, условие их пересечения.
6. Напишите следующие уравнения прямой на плоскости: уравнение прямой с угловым коэффициентом, общее уравнение прямой, нормальное уравнение. Как найти угол между прямыми? Каковы условия параллельности и перпендикулярности прямых?
7. Дайте определение окружности, эллипса, гиперболы, параболы и напишите их канонические уравнения.
8. Начертите полярную систему координат и запишите формулы, связывающие прямоугольные и полярные координаты точки.
9. Дайте определение матрицы. Укажите, как они складываются. умножаются. Дайте определение обратной матрицы. Как найти обратную матрицу? Запишите систему линейных уравнений в матричной форме и объясните матричный метод ее решения.
10. Дайте определение функции. Что называется областью определения функции и каковы основные способы задания функции? Что называется графиком функции? Какие функции называются четными, нечетными, периодическими и каковы особенности их графиков?
11. Начертите графики основных элементарных функции. Сформулируйте определение предела функции при стремлении аргумента к конечному пределу и при стремлении аргумента к бесконечности.
12. Как связано понятие предела функции спонятиями ее пределовслева и справа?
13. Какая функция называется бесконечно малойи каковы ее основныесвойства?
14. Какая функция называетсябесконечно большой и какова ее связь с бесконечно малой?
15. Сформулируйте основные теоремы о пределах.
16. Что такое первый и второй замечательные пределы?
17. Сформулируйте определения непрерывности функции в точке и на отрезке. Какие точки называются точками разрыва функции?
18. Сформулируйте определение производной. Каков ее механический и геометрический смысл?
19. Запишите формулы производных суммы, произведения, частного двух функций и таблицу производных.
20. Сформулируйте правило дифференцирования сложной функции и теорему о дифференцировании обратной функции.
21. Что такое логарифмическое дифференцирование?
22. Как находятся производные функций, заданных параметрически?
23. Сформулируйте определение дифференциала функции. Каков его геометрический смысл?
24. Сформулируйте теоремы Ролля и Лагранжа. Каков их геометрический смысл?
25. В чем состоит правило Лопиталя для раскрытия неопределенностей?
КОНТРОЛЬНАЯ РАБОТА №1
Задача №1
Даны координаты вершин треугольника 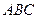 . Найти:
. Найти:
1) уравнения сторон 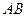 и
и 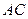 и их угловые
и их угловые
коэффициенты;
2) угол 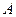 в радианах (градусах) с точностью до двух знаков после запятой;
в радианах (градусах) с точностью до двух знаков после запятой;
3) уравнение высоты 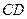 и ее длину;
и ее длину;
4) уравнение медианы 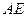 и координаты точки
и координаты точки 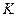 пересечения этой медианы с высотой
пересечения этой медианы с высотой 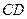 .
.
Сделать чертеж.
| Номер варианта | А | В | С |
| (2;5) | (14;-4) | (18;18) | |
| (0;3) | (12;-6) | (10;8) | |
| (-9;6) | (3;-3) | (7;19) | |
| (-12;-1) | (0;-10) | (4;12) | |
| (4;1) | (16;-8) | (14;6) | |
| (-3;10) | (9;1) | (7;15) | |
| (-1;4) | (11;-5) | (15;17) | |
| (3;6) | (15;-3) | (13;11) | |
| (-2;7) | (10;-2) | (8;12) | |
| (-6;8) | (6;-1) | (4;13) | |
| (-5;9) | (7;0) | (5;14) | |
| (-8;-3) | (4;-12) | (8;10) | |
| (-5;7) | (7;-2) | (11;20) | |
| (-4;10) | (8;1) | (12;23) | |
| (-7;4) | (5;-5) | (3;9) | |
| (0;2) | (12;-7) | (16;15) | |
| (-10;-9) | (2;0) | (6;22) | |
| (1;0) | (13;-9) | (17;13) | |
| (-4;12) | (8;3) | (6;17) | |
| (-10;5) | (2;-4) | (0;10) |
Задача №2
Даны координаты вершин пирамиды 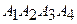 . Найти:
. Найти:
1) длину ребра 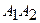 ;
;
2) угол между ребрами 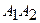 и
и 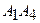 ;
;
3) уравнение плоскости 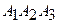 и угол между ребром
и угол между ребром
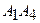 и плоскостью
и плоскостью 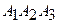 ;
;
4) уравнение высоты, опущенной из вершины 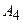 на грань
на грань
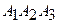 и ее длину;
и ее длину;
5) площадь грани 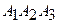 и объем пирамиды.
и объем пирамиды.
Сделать чертеж.
| Номер варианта | 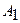 | 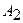 | 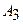 | 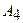 |
| (5;3;10) | (1;9;7) | (0;2;0) | (4;3;5) | |
| (2;3;5) | (5;3;7) | (4;2;10) | (1;2;7) | |
| (4;10;9) | (1;8;2) | (5;7;4) | (5;2;6) | |
| (2;5;8) | (1;4;9) | (2;1;6) | (5;4;2) | |
| (4;4;10) | (7;10;2) | (2;8;4) | (9;6;9) | |
| (2;3;9) | (3;3;6) | (2;1;7) | (1;2;5) | |
| (8;7;4) | (5;10;4) | (4;7;8) | (3;5;4) | |
| (2;6;5) | (1;2;5) | (4;0;6) | (6;4;8) | |
| (–2;8;2) | (6;8;9) | (5;3;3) | (7;10;3) | |
| (2;1;3) | (4;–1;1 ) | (1;0;–1) | (0;1;1) | |
| (0;2;7) | (1;5;0) | (0;7;1) | (4;2;5) | |
| (1;8;9) | (-1;3;0) | (4;7;8) | (2;4;9) | |
| (5;3;7) | (2;3;5) | (4;2;10) | (1;2;7) | |
| (8;6;4) | (2;1;1) | (5;6;8) | (8;10;7) | |
| (3;2;8) | (2;–1;7) | (6;3;1) | (2;–3;7) | |
| (5;3;1) | (2;3;7) | (7;2;2) | (5;7;7) | |
| (3;5;8) | (6;5;8) | (7;7;3) | (8;4;1) | |
| (–1;0;3) | (4;2;1) | (1;2;7) | (4;1;3) | |
| (6;9;4) | (7;5;9) | (4;6;5) | (1;5;5) | |
| (6;9;3) | (6;6;5) | (4;6;11) | (4;9;5) |
Задача №3
Сделать чертеж и составить уравнение линий:
1) расстояние каждой точки которой от начала координат и от точки 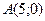 относятся как
относятся как 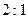 ;
;
2) расстояние каждой точки которой от точки 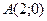 и от прямой
и от прямой 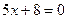 относятся как
относятся как 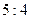 ;
;
3) расстояние каждой точки которой от точки 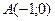 вдвое меньше расстояния ее от прямой
вдвое меньше расстояния ее от прямой 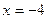 ;
;
4) для каждой точки которой расстояние от начала координат и от точки 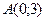 относятся друг к другу как
относятся друг к другу как 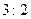 ;
;
5) каждая точка которой находится втрое дальше от точки 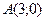 , чем от точки
, чем от точки 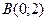 ;
;
6) расстояние каждой точки которой от точки 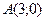 вдвое меньше расстояния ее от точки
вдвое меньше расстояния ее от точки 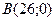 ;
;
7) для каждой точки которой расстояние от точки 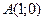 и от прямой
и от прямой 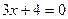 относятся как
относятся как 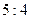 ;
;
8) каждая точка которой отстоит от точки 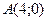 втрое дальше, чем от начала координат;
втрое дальше, чем от начала координат;
9) для каждой точки которой сумма квадратов расстояний до сторон квадрата с вершинами 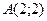 ,
, 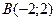 ,
, 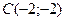 ,
, 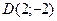 есть величина постоянная, равная
есть величина постоянная, равная 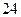 ;
;
10) каждая точка которой одинаково удалена от точки 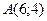 и от прямой
и от прямой 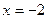 ;
;
11) каждая точка которой одинаково удалена от точки 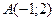 и от оси
и от оси 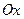 .
.
12) для каждой точки которой сумма квадратов расстояний до точек 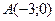 и
и 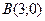 равна
равна 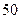 ;
;
13) для каждой точки которой сумма квадратов расстояний до точек 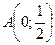 и
и 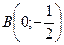 равна
равна 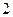 ;
;
14) расстояние каждой точки которой от точки 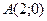 и от прямой
и от прямой 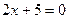 относятся как
относятся как 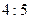 ;
;
15) расстояние каждой точки которой от точки 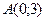 втрое больше расстояния от точки
втрое больше расстояния от точки 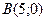 ;
;
16) каждая точка которой равноудалена от точки 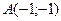 и от прямой
и от прямой 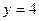 ;
;
17) для каждой точки которой отношение расстояния до точки 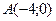 к расстоянию до прямой
к расстоянию до прямой 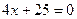 равно
равно 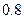 ;
;
18) каждая точка которой одинакова удалена от точки 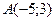 и от начала координат;
и от начала координат;
19) каждая точка которой находится вдвое дальше от точки 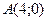 , чем от точки
, чем от точки 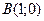 ;
;
20) полученной при таком движении точки 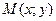 , что расстояние от нее до точки
, что расстояние от нее до точки 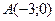 вдвое меньше расстояния от точки
вдвое меньше расстояния от точки 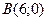 ;
;
Задача №4
Решить систему линейных уравнений методом Гаусса.
1. 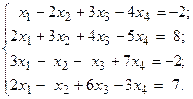 2.
2. 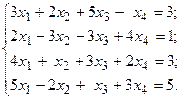
3. 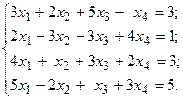 4.
4. 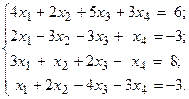
5. 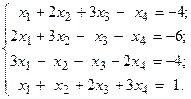 6.
6. 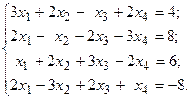
7. 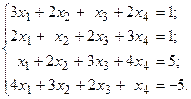 8.
8. 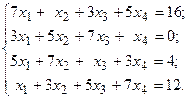
9. 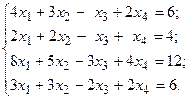 10.
10. 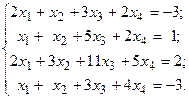
11. 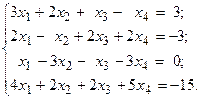 12.
12. 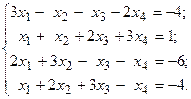
13. 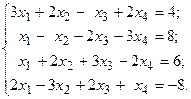 14.
14. 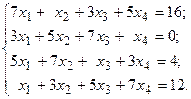
15. 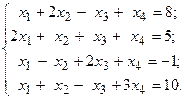 16.
16. 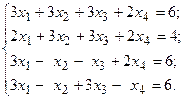
17. 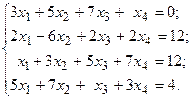 18.
18. 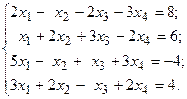
19. 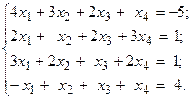 20.
20. 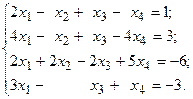
Задача №5
Решить систему линейных уравнений двумя способами:
1) методом Крамера;
2) используя обратную матрицу.
1. 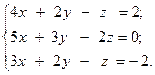 2.
2. 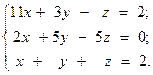
3. 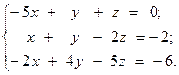 4.
4. 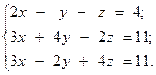
5. 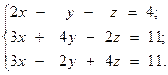 6.
6. 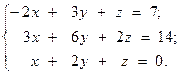
7. 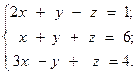 8.
8. 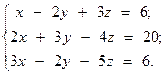
9. 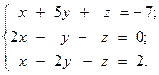 10.
10. 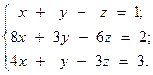
11. 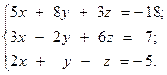 12.
12. 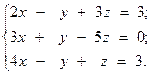
13. 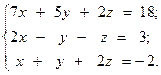 14.
14. 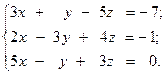
15. 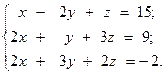 16.
16. 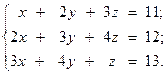
17. 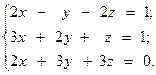 18.
18. 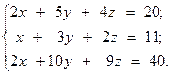
19. 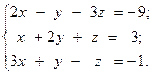 20.
20. 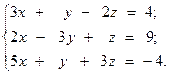
Задача №6
Вычислить пределы, не пользуясь правилом Лопиталя.
1. a) 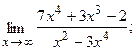 б)
б) 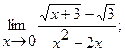
в) 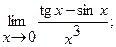 г)
г) 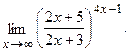
2. a) 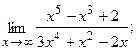 б)
б) 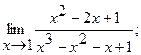
в) 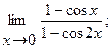 г)
г) 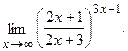
3. a) 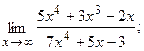 б)
б) 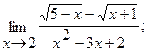
в) 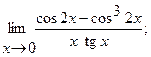 г)
г) 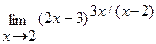 .
.
4. a) 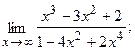 б)
б) 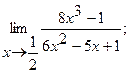
в) 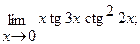 г)
г) 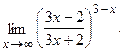
5. а) 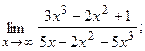 б)
б) 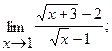
в) 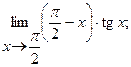 г)
г) 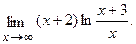
6. а) 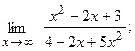 б)
б) 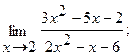
в) 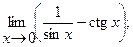 г)
г) 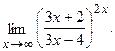
7.а)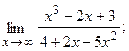 б)
б) 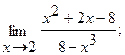
в) 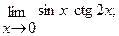 г)
г) 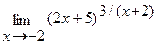 .
.
8. а) 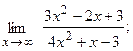 б)
б) 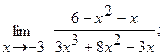
в) 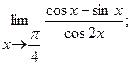 г)
г) 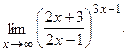
9. а) 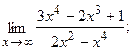 б)
б) 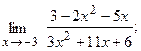
в) 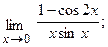 г)
г) 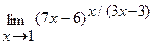 .
.
10. а) 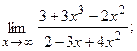 б)
б) 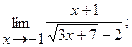
в) 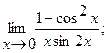 г)
г) 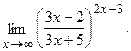
11.a) 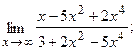 б)
б) 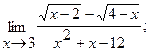
в) 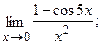 г)
г) 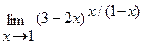
12.а) 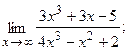 б)
б) 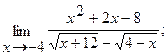
в) 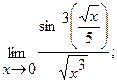 г)
г) 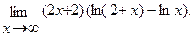
13.а) 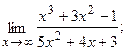 б)
б) 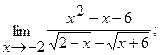
в) 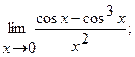 г)
г) 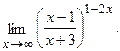
14.a) 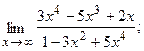 б)
б) 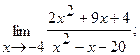
в) 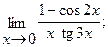 г)
г) 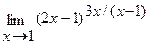 .
.
15.а) 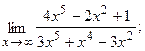 б)
б) 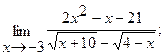
в) 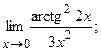 г)
г) 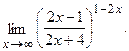
16. а) 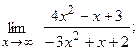 б)
б) 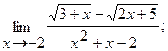
в) 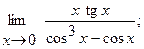 г)
г) 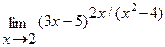 .
.
17.а)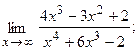 б)
б) 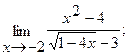
в) 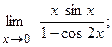 г)
г) 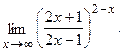
18. а) 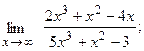 б)
б) 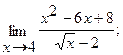
в) 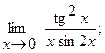 г)
г) 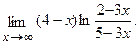
19. а) 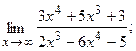 б)
б) 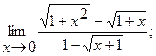
в) 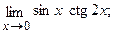 г)
г) 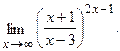
20. а) 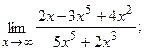 б)
б) 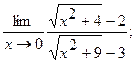
в) 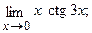 г)
г) 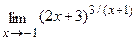 .
.
Задача №7
Исследовать функцию 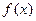 на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
на непрерывность. Определить характер точек разрыва, если они существуют. Сделать чертеж.
1. 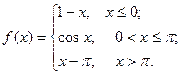 2.
2. 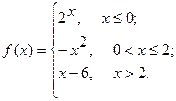
3. 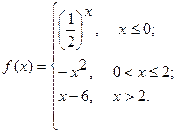 4.
4. 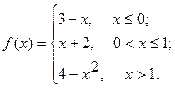
5. 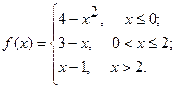 6.
6. 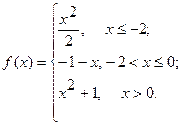
7. 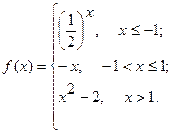 8.
8. 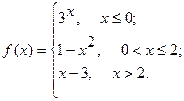
9. 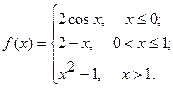 10.
10. 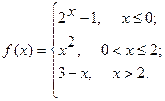
11. 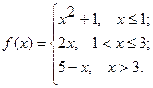 12.
12. 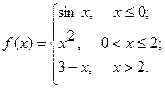
13. 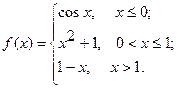 14.
14. 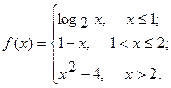
15. 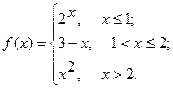 16.
16. 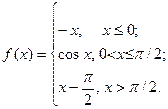
17. 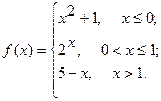 18.
18. 
19. 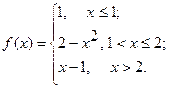 20.
20. 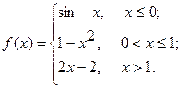
Задача №8
Найти производные заданных функций
1.a) 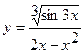 ; б)
; б) 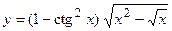 ;
;
в) 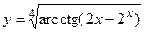 ; г)
; г) 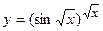 ;
;
д) 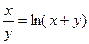 ; е)
; е) 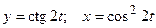 .
.
2. a) 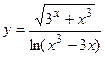 ; б)
; б) 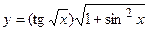 ;
;
в) 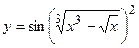 ; г)
; г) 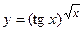 ;
;
д) 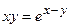 ; е)
; е) 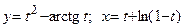 .
.
3. a) 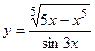 ; б)
; б) 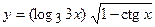 ;
;
в) 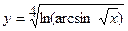 ; г)
; г) 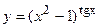 ;
;
д) 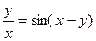 ; е)
; е) 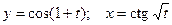 .
.
4. а) 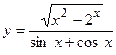 ; б)
; б) 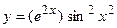 ;
;
в) 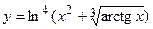 ; г)
; г) 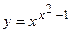 ;
;
д) 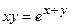 ; е)
; е) 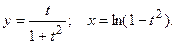
5. a) 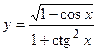 ; б)
; б) 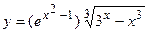 ;
;
в) 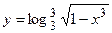 ; г)
; г) 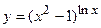 ;
;
д) 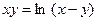 ; е)
; е) 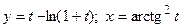 .
.
6. а) 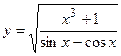 ; б)
; б) 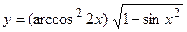 ;
;
в) 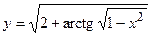 ; г)
; г) 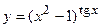 ;
;
д) 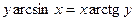 ; е)
; е) 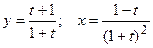 .
.
7. a) 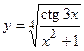 ; б)
; б) 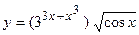 ;
;
в) 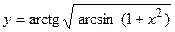 ; г)
; г) 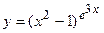 ;
;
д) 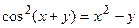 ; е)
; е) 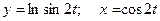 .
.
8. а) 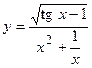 ; б)
; б) 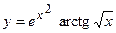 ;
;
в) 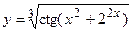 ; г)
; г) 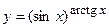 ;
;
д) 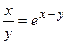 ; е)
; е) 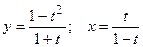 .
.
9. а) 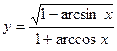 ; б)
; б) 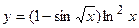 ;
;
в) 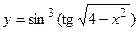 ; г)
; г) 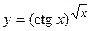 ;
;
д) 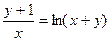 ; е)
; е) 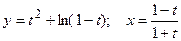 .
.
10. а) 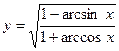 ; б)
; б) 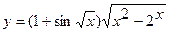 ;
;
в) 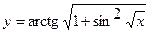 ; г)
; г) 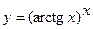 ;
;
д) 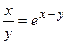 ; е)
; е) 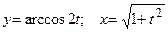 .
.
11. а) 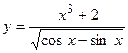 ; б)
; б) 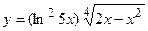 ;
;
в) 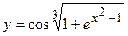 ; г)
; г) 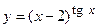 ;
;
д) 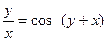 ; е)
; е) 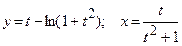 .
.
12. a) 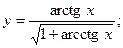 б)
б) 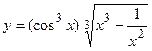 ;
;
в) 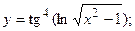 ; г)
; г) 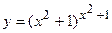 ;
;
д) 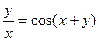 ; е)
; е) 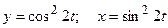 .
.
13. a) 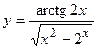 ; б)
; б) 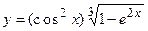 ;
;
в) 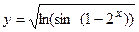 ; г)
; г) 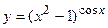 ;
;
д) 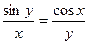 ; е)
; е) 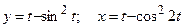 .
.
14. а) 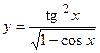 ; б)
; б) 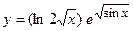 ;
;
в) 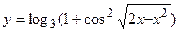 ; г)
; г) 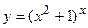 ;
;
д) 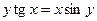 ; е)
; е) 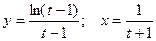 .
.
15. a) 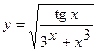 ; б)
; б) 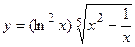 ;
;
в) 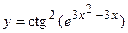 ; г)
; г) 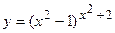 ;
;
д) 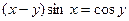 ; е)
; е) 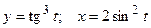 .
.
16. a) 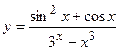 ; б)
; б) 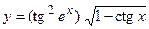
в) 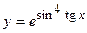 ; г)
; г) 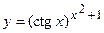 ;
;
д) 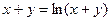 ; е)
; е) 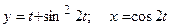 .
.
17. а) 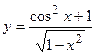 ; б)
; б) 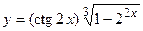 ;
;
в) 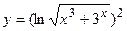 ; г)
; г) 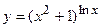 ;
;
д) 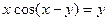 ; е)
; е) 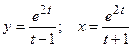 .
.
18. a) 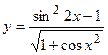 ; б)
; б) 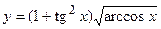 ;
;
в) 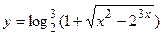 ; г)
; г) 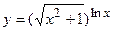 ;
;
д) 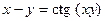 ; е)
; е) 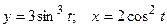 .
.
19. а) 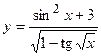 ; б)
; б) 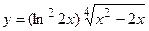 ;
;
в) 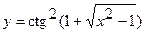 ; г)
; г) 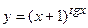 ;
;
д) 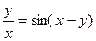 ; е)
; е) 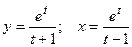 .
.
20. а) 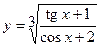 ; б)
; б) 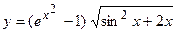 ;
;
в) 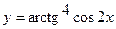 ; г)
; г) 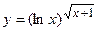 ;
;
д) 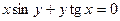 ; е)
; е) 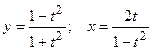 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ К КОНТРОЛЬНОЙ РАБОТЕ №1
Задача №1
Даны координаты вершин треугольника 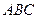 :
: 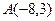 ,
, 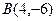 ,
, 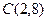 . Найти:
. Найти:
1) уравнения сторон 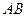 и
и 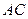 и их угловые
и их угловые
коэффициенты;
2) угол 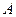 в радианах (градусах) с точностью до двух знаков после запятой;
в радианах (градусах) с точностью до двух знаков после запятой;
3) уравнение высоты 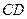 и ее длину;
и ее длину;
4) уравнение медианы 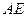 и координаты точки
и координаты точки 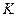 пересечения этой медианы с высотой
пересечения этой медианы с высотой 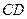 .
.
 Сделать чертеж (рис.1).
Сделать чертеж (рис.1).
Рис. 1
Решение. 1) Найдем координаты векторов 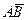 и
и 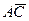 , для чего воспользуемся формулой
, для чего воспользуемся формулой
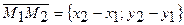 .
.
Тогда 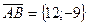 ,
, 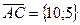 . Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
. Эти векторы являются направляющими векторами прямых, на которых лежат соответствующие стороны треугольника и для получения их уравнений можно использовать каноническое уравнение прямой на плоскости
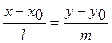 .
.
В результате получим
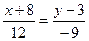 (
( 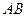 ),
),
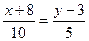 (
( 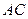 ).
).
Разрешая эти уравнения относительно 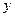 , т.е. приводя их к виду уравнения прямой с угловым коэффициентом
, т.е. приводя их к виду уравнения прямой с угловым коэффициентом
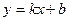 ,
,
найдем 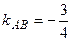 ,
, 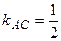 .
.
2) Угол 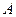 треугольника совпадает с углом между векторами
треугольника совпадает с углом между векторами 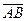 и
и 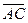 и для его нахождения можно использовать формулу
и для его нахождения можно использовать формулу
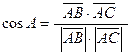 ,
,
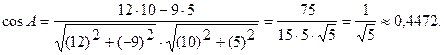 По таблице найдем значение угла
По таблице найдем значение угла 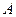 : <
: < 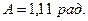 (
( 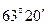 ).
).
3) Для получения уравнения высоты 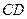 приведем уравнение стороны
приведем уравнение стороны 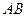 к виду общего уравнения прямой на плоскости
к виду общего уравнения прямой на плоскости
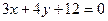 (
( 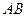 ).
).
Из рисунка видно, что вектор нормали к прямой 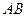 является направляющим вектором высоты
является направляющим вектором высоты
