Построение эмпирических формул методом наименьшего квадрата

Очень часто, особенно при анализе эмпирических данных возникает необходимость найти в явном виде функциональную зависимость между величинами x и y, которые получены в результате измерений.

При аналитическом исследовании взаимосвязи между двумя величинами x и y производят ряд наблюдений, в результате чего получается таблица значений:

Таблица 2. Таблица значений.

x			…		…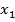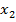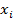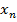
y			…		…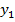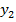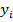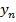

Эта таблица обычно получается как итог каких-либо экспериментов, в которых х_i (независимая величина) задается экспериментатором, а 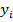получается в результате опыта. Поэтому эти значения 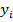будем называть эмпирическими или опытными значениями.

Между величинами x и y существует функциональная зависимость, но её аналитический вид обычно неизвестен, поэтому возникает практически важная задача – найти эмпирическую формулу

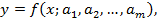(1)

значения которой при 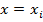возможно мало отличались бы от опытных значений .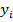

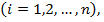
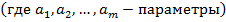Обычно указывают класс функций (например, множество линейных, степенных, показательных и т.п.) из которого выбирается функция 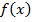и далее определяются наилучшие значения параметров.

Если в эмпирическую формулу (1) подставит исходные 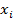, то получим теоретическое значение 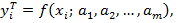где где i=1,2,…,n.

Разности 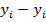называются отклонениями и представляют собой расстояния по вертикалям от точек 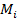до графика эмпирической функции.

Согласно методу наименьших квадратов, наилучшими коэффициентами 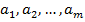считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функций

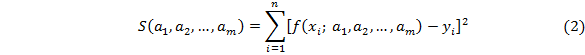
будет минимальной.

Поясним геометрический смысл метода наименьших квадратов.

Каждая пара чисел 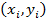из исходной таблицы определяет точку 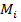на плоскости XOY. Используя формулу (1) при различных значениях коэффициентов 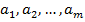можно построить ряд кривых, которые являются графиками функции (1). Задача состоит в определение коэффициентов 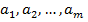таким образом, чтобы сумма квадратов расстояний по вертикали от точек 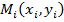до графика функции (1) была наименьшей (рис. 1).

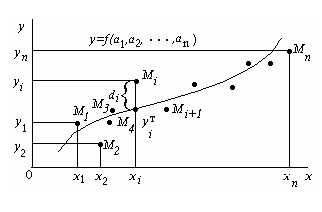
Рис.1 Графический смысл метода наименьших квадратов

Построение эмпирической формулы состоит из двух этапов: выяснение общего вида этой формулы и определения её наилучших параметров.

Если неизвестен характер зависимости между данными величинами x и y , то вид эмпирической зависимости является произвольным. Предпочтение отдается простым формулам, обладающим хорошей точностью. Удачный выбор эмпирической формулы в значительной мере зависит от знаний исследователя в предметной области, используя которые он может указать класс функций из теоретических соображений. Большое значение имеет изображение полученных данных в декартовых или в специальных системах координат (полулогарифмической, логарифмической и т.д.). По положению точек можно примерно угадать общий вид зависимости путем установления сходства между построенным графиком и образцами известных кривых.

Определение наилучших коэффициентов 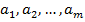, входящих в эмпирическую формулу, производят хорошо известными аналитическими методами.

Для того, чтобы набор коэффициентов 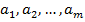, которые доставляют минимум функции S, определяемой формулой (2), используем необходимое условие экстремума функции нескольких переменных – равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов.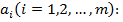

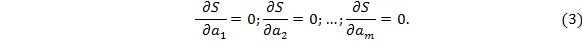
Таким образом, нахождение коэффициентов 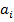сводиться к решению системы (3).

Эта система упрощается, если эмпирическая формула (1) линейна относительно параметров 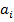, тогда система (3) - будет линейной.

Конкретный вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линейной зависимости 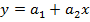система (3) примет вид:

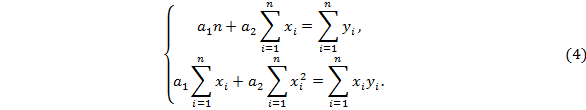
Эта линейная система может быть решена любым известным методом (методом Гаусса, простых итерации, формулами Крамера).

В случае квадратичной зависимости 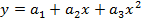система (3) примет вид:

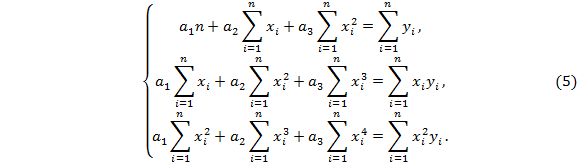
В случае экспоненциальной зависимости функция примет вид:

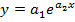(6)

В этом случае нужно вначале линеаризовать формулу (6) с помощью логарифмирования:

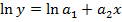(7)

Введем обозначения:

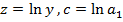(8)

Тогда уравнение (7) перепишется в виде: 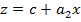, и система для определения параметров 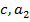примет вид:

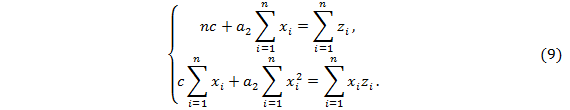
или, возвращаясь к табличным эмпирическим данным,

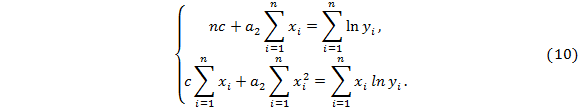
Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные, вводится характеристика - коэффициент детерминированности.

Для его описания рассмотрим следующие величины: 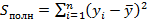– полная сумма квадратов, где 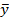среднее значение .

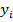Можно доказать следующее равенство: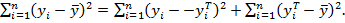

Первое слагаемое равно 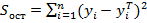и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.

Второе слагаемое равно 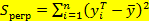и называется регрессивной суммой квадратов; оно характеризует разброс данных.

Очевидно, что справедливо следующее равенство .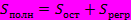

Коэффициент детерминированности определяется по формуле:

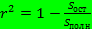(11)

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности 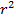, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.

Степень связи характеристик 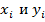предлагается оценить с помощью коэффициента корреляции:

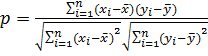(12)

Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае, когда выполняется равенство 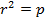то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные [1].

Исходные данные

Задание

Функция 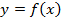задана таблицей 2:

Таблица 2 Исходные данные функции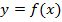

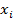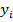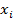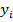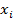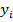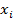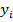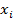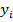0.51	4.57	3.33	15.11	4.87	20.87	7.44	32.15	9.87	41.82
1.11	6.22	3.39	16.03	5.35	23.83	7.98	33.32	10.65	43.76
1.62	8.99	3.51	16.51	5.94	26.18	8.87	37.84	10.76	45.36
2.65	13.09	3.99	18.42	6.87	26.76	8.90	37.96	11.03	45.97
2.74	13.45	4.42	20.13	7.12	30.88	9.54	42.65	11.76	49.34

Требуется выяснить – какая из функций – линейная, квадратичная или экспоненциальная наилучшим образом аппроксимирует функцию, заданную таблицей 2.