Формулы вычисления производных
1) (с)'=0, где с – число
2) (хр)′=р·хр-1
3) (х)'=1
4) (ех)′=ех
5) (lnx)′= 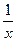 , х>0
, х>0
6) (sinx)′=cosx
7) (cosx)′=-sinx
8) (ах)′=ахlnx
9) (logax)′= 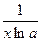
Производная сложной функции
Если f (g(х)) - сложная функция, то ее производная равна произведению производных внешней и внутренней функций, т.е. [f(g(x))]'= f '(g) ◦ g'(x).
1) (up)'=p∙up-1∙u'
2) (eu)'=eu∙u'
3) sinu)'=cosu∙u'
4) (cosu)'=-sinu∙u'
5) (lnu)'= 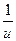 ∙u'
∙u'
Производная произведения и частного
1) Если функции u и v дифференцируемы в точке x0, то их произведение также дифференцируемо в точке x0 причем
(u∙v)'= u'∙v+ u∙ v'
2) Если функции u и n дифференцируемы в точке х0 и
n'(x0) ≠ 0, то их частное также дифференцируемо в точке x0, причем
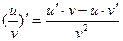
3) Если функция и дифференцируема в точке x0 и с = const. то их произведение также дифференцируемо в точке x0 причем (сu)' = с∙u'.
Геометрический смысл производной
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x0 .
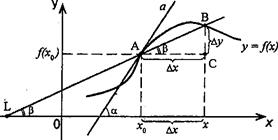
Рассмотрим произвольную прямую, проходящую через точку графика функции - точку А(x0, f (х0)) и пересекающую график в некоторой точке 'B(x;f(x)).
Геометрический смысл производной заключается в следующем:
Производная функции в точке x0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x0.
\
2. Примеры и упражнения
Пример 1 : Найти производную функции:
a) (2х5)′=2∙5х5-1=10х4
b) (4х12)′=4∙12х12-1=48х11
c) (3х4+2х15)′=(3х4)′+(2х15)′=3∙4х3+2∙15х14=12х3+30х14
d) (3х2+4х-46)′= (3х2)′+(4х)′-(46)′=3∙2х+4∙1-0=6х+4
e) (6cosx –2sinx+5ex)′= (6cosx)′ –(2sinx)′+(5ex)′=6∙(-sinx)-2∙cosx +5∙ex= =6sinx-2cosx+5ex
f) (23lnx-12x4)′= (23lnx)′-(12x4)′=23∙ 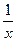 -12∙4х3=
-12∙4х3= 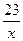 -48х3
-48х3
g) ((3х+15)7)'=7∙(3х+15)7-1∙(3х+15)'=7∙(3х+15)6∙(3)=21(3х+15)6
h) ((5х-7)∙(4+3x))'= (5х-7)'∙(4+3х)+ (5х-7) ∙ (4+3х)'=
5∙(4+3х)+(5х-7)∙4=20+15х+20х-28=35х-8
i) 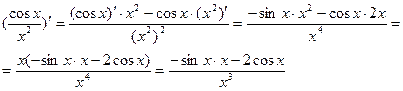
j) (sin( 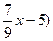 )'=cos(
)'=cos( 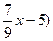 ∙(
∙( 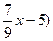 )'= cos(
)'= cos( 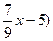 ∙
∙ 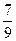 =
= 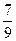 cos(
cos( 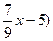
Пример 2:Вычислить значение производной в точке
а)Найти; 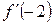 ,если
,если 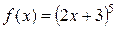
Решение:
f'(x)= ((2х+3)5)'=5∙(2х+3)5-1∙(2х+3)'=5∙(2х+3)4∙(2)=10(2х+3)4
f'(-2)= 10(2∙(-2)+3)4=10(-1)4=10
Ответ: f'(-2)=10
b) Найти; 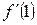 ,еслиf(x) =
,еслиf(x) = 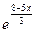
Решение:
f'(x)= (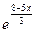 )'=
)'=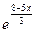 ∙(
∙( 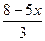 )'=
)'=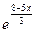 ∙(
∙( 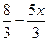 )'=
)'=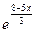 ∙(
∙( 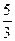 )=
)= 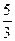
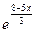
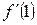 =
= 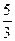
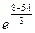 =
= 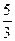 e
e
Ответ: 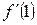 =
= 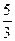 e
e
Пример 3:Найти угловой коэффициент касательной к графику функции у=f(х) в точке х0.
f(х) = 5х3-6х2+8х-10 , х0=1
Решение:
к= f'(x0)- угловой коэффициент касательной
f'(x)= (5х3-6х2+8х-10)'=15х2-12х+8
к= f'(x0)= f'(1)=15∙12-12∙1+8=11
Ответ: к=11
Пример 4: Написать уравнение касательной к графику функции у=f(х) в точке х0
у= 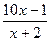 , х=1
, х=1
Решение :
у= f(x0)+ f'(x0)∙(х-х0) – уравнение касательной
f(x0)= f(1)= 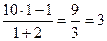
f'(x)=( 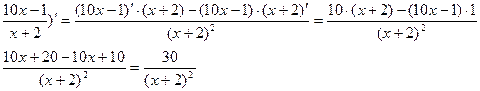
f'(x0)= f'(1)= 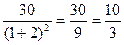
у= f(x0)+ f'(x0)∙(х-х0)=3+ 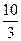 (х-1)=3+
(х-1)=3+ 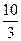 х-
х- 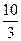 =
= 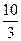 х-
х- 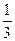 - уравнение касательной
- уравнение касательной
Ответ: у= 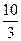 х-
х- 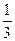 - уравнение касательной
- уравнение касательной
Варианты контрольной работы
Задание 1: Найти производную
Вариант 1: 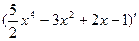 ,
, 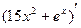 ,
, 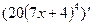 ,
, 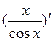
Вариант 2: 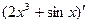 , (15ех-4lnx)' ,
, (15ех-4lnx)' , 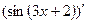 ,
, 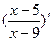
Вариант 3: 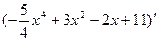 ,
, 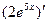 ,
, 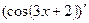
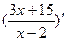
Вариант 4: 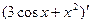 ,
, 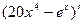 ,
, 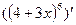 ,
, 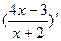
Вариант 5:( 3x 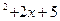 )',
)', 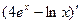 , (sinx-5cosx)', (
, (sinx-5cosx)', ( 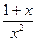 )'
)'
Вариант 6: ( 6x 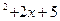 )', (20 sin x - 7 cos x + 1)' ,( ln(x
)', (20 sin x - 7 cos x + 1)' ,( ln(x 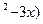 )' , (
)' , ( 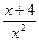 )'
)'
Вариант 7: 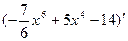 , (sin (3x+2))',
, (sin (3x+2))', 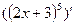 ,
, 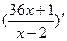
Вариант 8: 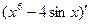 ,
, 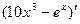
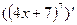
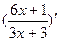
Вариант 9: 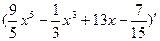 ,
, 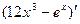 ,
, 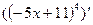
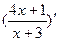
Вариант 10: 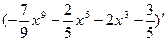 ,
, 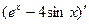 ,
, 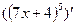 ,
, 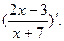
Вариант 11: ( 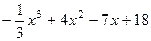 )' (sin( 53x+2))',
)' (sin( 53x+2))', 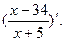
Вариант 12: 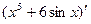 ,
, 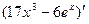
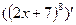
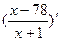
Вариант 13: ( 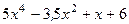 )',
)', 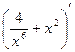 , (sin (3x+2))' ,
, (sin (3x+2))' , 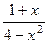 )'
)'
Вариант 14: ( 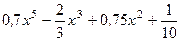 )' ,(5ех)' , (
)' ,(5ех)' , ( 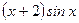 )' , (
)' , ( 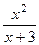 )'.
)'.
Вариант 15: ( 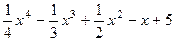 )' ,
)' , 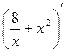 , (sin( 53x+2))',((2х-3)∙(3х+6))'
, (sin( 53x+2))',((2х-3)∙(3х+6))'
Вариант 16:(8x – 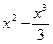 )', (6lnx-45)' ,
)', (6lnx-45)' , 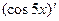 ; (
; ( 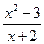 )'
)'
Вариант 17: (2x- 3)' , (65ех)' , ( 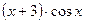 )' , (
)' , ( 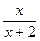 )'.
)'.
Вариант 18: ( 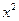 + 2)' ,
+ 2)' , 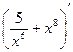 ,
, 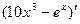 , ((5х-2)∙( х+6))'
, ((5х-2)∙( х+6))'
Вариант 19: (x4-3x2-7)' , (7lnx-х)' , 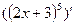 , ((6х-3)∙(8х+6))'
, ((6х-3)∙(8х+6))'
Вариант 20: (4x3-6x)' , (2sin(2x-4))' , ( 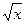 )' ,((5х-4)5)'
)' ,((5х-4)5)'
Вариант 21:( 3х2+5х-6)' , (cos(2x-4)' , ((5х-4)5)' , ((7х-3)∙( х+6))'
Вариант 22: ((х-3)(х+4))' , (2х4 )' , ((3х+1)6 )' , ( 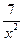 )'
)'
Вариант 23: (3х2-5х+1)' , ((х+5)(х-4))' , ( 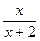 )' ,
)' , 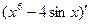
Вариант 24: ( 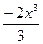 +х2+12)' , (6lnx-45)' ,
+х2+12)' , (6lnx-45)' , 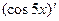 , (
, ( 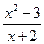 )'
)'
Вариант 25: (х3-х4)' , 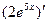 ,
, 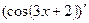 ,
, 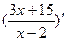
Вариант 26: 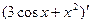 ,
, 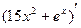 ,
, 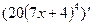 ,
, 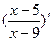
Вариант 27: ( 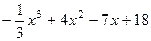 )' ,
)' , 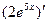 ,
, 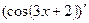 ,
, 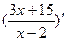
Вариант 28: 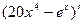 ,
, 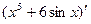 ,
, 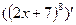 ,
, 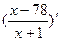
Вариант 29: 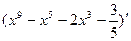 ,
, 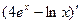 , (sin( 53x+2))', (
, (sin( 53x+2))', ( 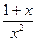 )'
)'
Вариант 30: 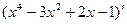 ,
, 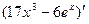 ,
, 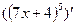 ,
, 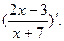
Задание 2: Вычислить значение функции
Вариант 1: Найти значение производной функции 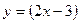 в точке
в точке 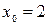 .
.
Вариант 2: Найти значение производной функции 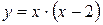 в точке
в точке 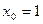 .
.
Вариант 3: Найти значение производной функции 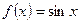 в точке
в точке 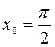 .
.
Вариант 4: Найти значение производной функции 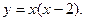 в точке
в точке 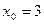 .
.
Вариант 5: Найти значение производной функции 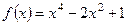 в точке
в точке 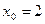 .
.
Вариант 6: Найти значение производной функции у= 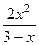 в точке
в точке 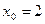 .
.
Вариант 7: Найти значение производной функции у= 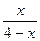 в точке
в точке 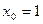 .
.
Вариант 8: Найти значение производной функции 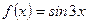 в точке
в точке 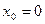 .
.
Вариант 9: Найти значение производной функции y(x)=5x7-8x в точке x0=1
Вариант 10: Найти значение производной функции y(x)=x2-3x в точке x0=-78
Вариант 11: Найти значение производной функции у=3х3 в точке х0=10
Вариант 12: Найти значение производной функции y(x)= 6x5-4x3+6x2 в точке x0=1
Вариант 13: Найти значение производной функции y(x)= x5-x3+2x2в точке x0=1
Вариант 14: Найти значение производной функции y(x)= x6-x4+6x3-3в точке x0=1
Вариант 15: Найти значение производной функции y(x)= x6-x4+6x3-3в точке x0=1
Вариант 16: Найти значение производной функции f (x) = (x2 + 1)(x3 – x) в точке х0=2
Вариант 17: Найдите значение производной функции 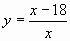 в точке х0 = 3.
в точке х0 = 3.
Вариант 18: Найти значение производной функции 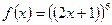 в точке x0=1
в точке x0=1
Вариант 19: Найти значение производной функции y(x)= 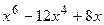 в точке x0=2
в точке x0=2
Вариант 20: Найти значение производной функции y(x)= 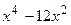 в точке x0=-2
в точке x0=-2
Вариант 21: Найти значение производной функции 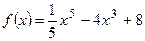 в точке x0=-2
в точке x0=-2
Вариант 22: Найти значение производной функции 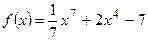 в точке x0=-1
в точке x0=-1
Вариант 23: Найти значение производной функции y(x)= 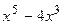 в точке x0=1
в точке x0=1
Вариант 24: Найти значение производной функции y(x)= 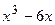 в точке x0=4
в точке x0=4
Вариант 25: Найти значение производной функции y = 12 cos x в точке x0= 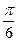
Вариант 26: Найти значение производной функции y(x)=x6-13x4+11 в точке x0=1
Вариант 27: Найти значение производной функции y(x)= 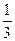 x3+x2+2x; в точке x0=-3
x3+x2+2x; в точке x0=-3
Вариант 28: Найти значение производной функции y(x)= 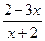 в точке x0=1
в точке x0=1
Вариант 29: Найти значение производной функции y(x)= 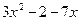 в точке x0=6
в точке x0=6
Вариант 30: Найти значение производной функции 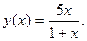 в точке x0=2
в точке x0=2
Задание 3
Вариант 1: Найдите угловой коэффициент касательной, проведенной к графику функции 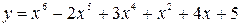 в точке
в точке 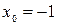 .
.
Вариант 2: Найдите угловой коэффициент касательной, проведенной к графику функции 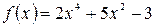 в точке с абсциссой
в точке с абсциссой 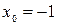 .
.
Вариант 3: Найдите угловой коэффициент касательной, проведенной к параболе 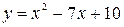 в точке с абсциссой
в точке с абсциссой 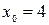 .
.
Вариант 4: Найдите угловой коэффициент касательной, проведенной к графику функции 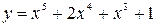 в точке
в точке 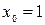 .
.
Вариант 5: Найдите угловой коэффициент касательной, проведенной к графику функции 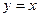 в точке
в точке 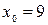 .
.
Вариант 6: Найдите угловой коэффициент касательной, проведенной к графику функции 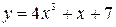 в точке
в точке 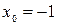 .
.
Вариант 7: Найдите значение производной функции 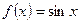 в точке
в точке 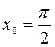 .
.
Вариант 8: Найдите угловой коэффициент касательной к графику функции 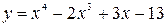 в точке
в точке 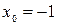 .
.
Вариант 9: Написать уравнение касательной к графику функции в точке х0 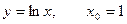
Вариант 10: Напишите уравнения касательной к графику функции 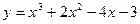 , в точке х0 =5.
, в точке х0 =5.
Вариант 11: Напишите уравнения касательной к графику функции 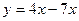 в точке
в точке 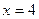 .
.
Вариант 12: Найти угловой коэффициент касательной к графику функции 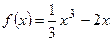 в точке
в точке 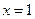
Вариант 13: Найти угловой коэффициент касательной, проведенной к графику функции y(x)=5x4-7 в точке 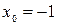
Вариант 14: Найти угловой коэффициент касательной, проведенной к графику функции 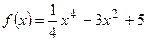 в точке
в точке 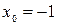
Вариант 15: Напишите уравнения касательной к графику функции у= 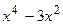 в точке
в точке 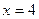 .
.
Вариант 16: Напишите уравнения касательной к графику функции
у= 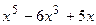 в точке
в точке 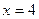 .
.
Вариант 17: Найти угловой коэффициент касательной, проведенной к графику функции 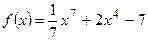 в точке
в точке 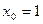
Вариант 18: Напишите уравнения касательной к графику функции
у= 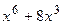 в точке
в точке 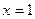 .
.
Вариант 19: Напишите уравнения касательной к графику функции
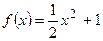 в точке
в точке 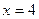 .
.
Вариант 20:Найти угловой коэффициент касательной к графику функции 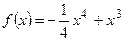 в точке
в точке 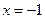
Вариант 21: Напишите уравнения касательной к графику функции 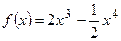 в точке
в точке 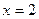 .
.
Вариант 22: Напишите уравнения касательной к графику функции f(x) = x3 – 6x2  в точке
в точке 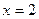 .
.
Вариант 23: Найти угловой коэффициент касательной к графику функции y = x5+19 x3+ 61 в точке 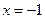
Вариант 24: Напишите уравнения касательной к графику функции f(x) = 2x4 - 8x3 в точке 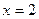
Вариант 25: Напишите уравнения касательной к графику функции f(x) = 4x2+10 в точке х=4
Вариант 26: Напишите уравнения касательной к графику функции f(x) = 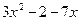 в точке х=5
в точке х=5
Вариант 27: Напишите уравнения касательной к графику функции 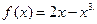 в точке х=3
в точке х=3
Вариант 28: Напишите уравнения касательной к графику функции f(x) = 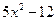 в точке х=7
в точке х=7
Вариант 29: Напишите уравнения касательной к графику функции 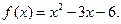 в точке х=5
в точке х=5
Вариант 30: Напишите уравнения касательной к графику функции f(x)=- 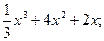 в точке х=3
в точке х=3
Содержание темы «Применение производной функции»
Нахождение стационарных точек и промежутков монотонности.
Достаточный признак убывания (возрастания) функции, теорема Лагранжа, понятия «промежутки монотонности функции»
Экстремумы функции и значения в них
Определения точек максимума и минимума, необходимый признак экстремума (теорему Ферма) и достаточный признак максимума и минимума, знать определения стационарных и критических точек функции
Исследование и построение графиков функций.
Схема исследования функции, метод построения графика чётной (нечётной) функции
Нахождение наибольших и наименьших значений функций.
Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке и на интервале
Основные сведения из теории
Экстремумы функции
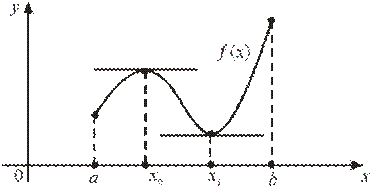
Определение: Точка х0 называется точкой максимума т.max функции f(х) если для всех х из некоторой окрестности точки х0 выполняется неравенство f(х) ≤ f(х0)
Другими словами: т.max – точка, выше которой график не поднимается
(в примере: х=4 –т.max)
Определение: Точка х0 называется точкой минимума т.min функции f(х) если для всех х из некоторой окрестности точки х0 выполняется неравенство f(х) ≥ f(х0)
Другими словами: т.min – точка, ниже которой график не опускается
(в примере: х=-1 –т.min)
Определение: Точки минимума т.min и точки максимума т.maxназываются точками экстремума функции.
Теорема Ферма: Пусть функция f(х) определена в некоторой окрестности точки х0 и дифференцируема в этой точке. Если х0 – точка экстремума функции f(х), то f′(х0)=0.
Другими словами: Необходимое условие существования точек экстремума: f′(х0)=0
 |  |
Алгоритм нахождения точек экстремума функции (т.max, т.min):
1) Найти интервалы возрастания и убывания функции:
- Найти производную функции f′(х);
- Найти стационарные точки (точки, в которых производная f(х) равна нулю), т.е. решить уравнение f′(х)=0;
- Отметить эти точки на числовой оси, указать промежутки;
- Выявить знаки производной f′(х) на каждом из полученных промежутков (подставить любое число из проверяемого промежутка в производную и узнать знак);
- Записать ответ.
2) По схеме определить точки максимума и точки минимума.
