Решение показательных уравнений

Определение: Показательным уравнением называется уравнение, в котором неизвестное содержится в показателе степени.

Теорема: Если а^х=а^в, где а>0, а≠1, то х = в

Решение показательных неравенств

Определение: Показательным неравенством называется неравенство, в котором неизвестное содержится в показателе степени.

Теорема: Если а^х>а^в, где, а≠1, то

1) Если а>0, то х > в, то есть знак сохраняется

2) Если а<0, то х < в, то есть знак меняется

2. Примеры и упражнения

Пример 1: Упростить выражение:

1)

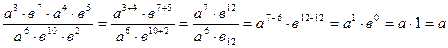
2)

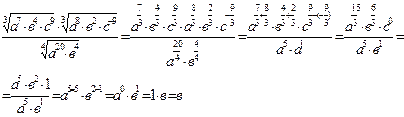
Пример 2:Решить показательное уравнение:

4^х-8=64

Решение:

4^х-8=4³

х-8=3

х=3+8

х=11

Ответ :х=11

Пример 3:Решить показательное уравнение:

3^х+2+3^х=90

Решение:

3^х·3²+3^х=90 t=9

Пусть 3^х=t,t>0 3^х=9

t·3²+t=90 3^х=3²

9t+t=90 х=2

10t=90 Ответ: х=2

t=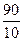

t=9

Пример 4: Решить показательное уравнение:

2^х-1+2^х=6

Решение:

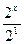+2^х=6

Пусть 2^х=t,t>0 t=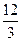

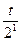+t=6 t=4

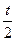+t=6 2^х=4

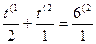2^х=2²

1t+2t=12 х=2

3t=12 Ответ: х=2

Пример 5: Решить показательное уравнение:

3^х+1-4·3^х-2=69

Решение:

3^х·3¹-4· 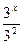=69

Пусть 3^х=t,t>0 t=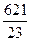

t·3¹-4· 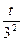=69 t=27

3t- 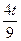=69 3^х=27

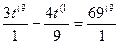3^х=3³

27t-4t=621 х=3

23t=621 Ответ: х=3

Пример 6: Решить показательное уравнение:

9^х +8·3^х –9 = 0

Решение:

(3²)^х+8·3^х –9 = 0

(3^х)²+8·3^х –9 = 0

Пусть 3^х =t, t > 0

t² +8· t –9 =0

а=1, b=8, с=-9

t_{1,2= =}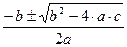

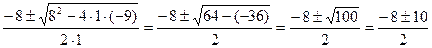
t₁= 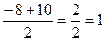t₂=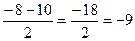

t₁= 1 t₂= -9, не уд., так как t>0

3^х = 1

3^х =3⁰

х=0

Ответ: х=0

Пример 7: Решить показательное неравенство:

2^3х-5>16

Решение:

2^3х-5>2⁴, т.к. 2>1, то знак сохраняем

3х-5>4

3х>4+5

3х>9

х>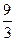

х>3, Ответ: х>3

Пример 8:Решить показательное неравенство:

3^х+2+3^х-1<28

Решение:

3^х·3²+ 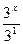<28

Пусть 3^х=t,t>0 t<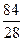

t·3²+ 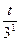<28 t<3

9t+ 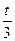<28 3^х<3

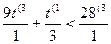3^х<3¹, т.к.3>1, то знак сохраняем

27t+t<84 х<1

28t<84 Ответ: х<1

Варианты контрольной работы

Задание 1: Упростить выражения

Вариант 1: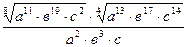

Вариант 2: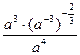

Вариант 3: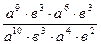

Вариант 4: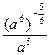

Вариант 5: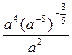

Вариант 6: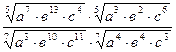

Вариант 7: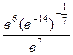

Вариант 8: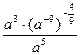

Вариант 9: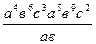

Вариант 10: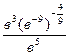

Вариант 11: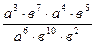

Вариант 12: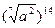

Вариант 13: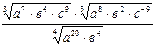

Вариант14: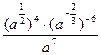

Вариант 15: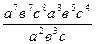

Вариант 16: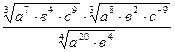

Вариант 17: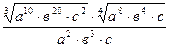

Вариант 18: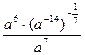

Вариант1 9: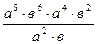

Вариант 20: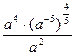

Вариант 21: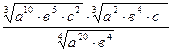

Вариант 22: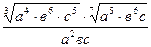

Вариант 23: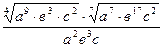

Вариант 24: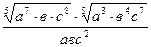

Вариант 25: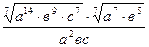

Вариант 26: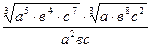

Вариант 27: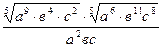

Вариант 28: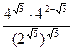

Вариант 29: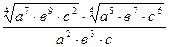

Вариант 30: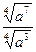

Задание 2: Решить показательное уравнение

Вариант 1:

3х+1=1

3х-2· 3х-2=7

Вариант 2:

4х+516

9· 3х-1+ 3х=36

Вариант 3:

4х=1	3х+2+3х=810

Вариант 4:

32х=3

4·3х+2+ 5·3х+1 -6·3х=5

Вариант 5:

3х=27

4х-3· 4х-2=13

Вариант 6:

3х·32=9

4· 3х-1+ 3х+1=117

Вариант 7:

17х=1

2х+1+2х-1=5

Вариант 8:

13х+1=13

2х+1+5·2х-2=104

Вариант 9:

4х=256	7х-7х-1=6
Вариант 10: 28х=16	5х+1-3·5х-2=122

Вариант 11:

3х+4=81

10·5х-1+ 5х+1=7

Вариант 12:

173х-5=17

8·2х-1- 2х=48

Вариант 13:

32+х=37

3х+1-4·3х-2=69

Вариант14:

164х=16

5х+1+5х+5х-1=31

Вариант 15:

4х-1=16

3х-3х-2=24

Вариант 16:

32х-1=1

4х+1+4х-2=260

Вариант 17:

53х=125

3х+2-5· 3х=36

Вариант 18:

17х-1=17

7х+2-14· 7х=5

Вариант1 9:

43х-4=16

5х+1+5х-2=630

Вариант 20:

(5х)2=25

2х+4-2х=120

Вариант 21:

9х+1=81

9Х-4·3х-45=0

Вариант 22:

43х+1=64

25Х-6·5х+5=0

Вариант 23:

52х+7=5

4х+2х+3-20=0

Вариант 24:

14х+5=1

4Х-14·2х-32=0

Вариант 25:

(3х)3=27

2х-23-х=7

Вариант 26:

15х+2=225

2·5х+2-10·5х=8

Вариант 27:

2х+4=8

3х-3+5х-1=10

Вариант 28:

52х=25

2х-2+2х-1+2х=14

Вариант 29:

4х=1	2·4х-5·2х+2=0

Вариант 30:

53х=125

3х+2-5· 3х=36

Задание 3: Решить показательное неравенство

Вариант 1:8^-2х< 64

Вариант 2: 3^1-х<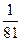

Вариант 3: 2^2х+1>8

Вариант 4: ( 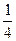)^х+1<

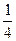
Вариант 5:4^2х+1>4

Вариант 6: 2^х+4-2^х>120

Вариант 7: ( )^4+6х< ^3х-3

Вариант 8: 8·2^х-1- 2^х>48

Вариант 9: 10^2+х< 100000

Вариант 10: 2^х+1+2^х-1<5

Вариант 11: 4· 3^х-1+ 3^х+1>117

Вариант 12: 5^х+4< 625

Вариант 13: 3^х+2+3^х810

Вариант14: 9· 3^х-1+ 3^х<36

Вариант 15:10^х+1< 1000000

Вариант 16: ( 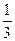)^6-3х> 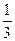^2х-1

Вариант 17: (6)^х-1>36^х-1

Вариант 18: 7^х-3< 49^х

Вариант1 9: 10^3х-1>1000

Вариант 20: 2^х-1< 16^х+2

Вариант 21: 2·5^х+2-10·5^х< 8

Вариант 22: 5^2-х< 25

Вариант 23: 5^1-3х<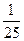

Вариант 24: 2^1-х>32^х

Вариант 25:( 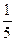)^4-2х< 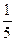^х+1

Вариант 26: 7^х+1>49^х

Вариант 27: 3^х-2· 3^х-2>7

Вариант 28: 4^х-3· 4^х-2<13

Вариант 29: 3^2-х< 27

Вариант 30: 10^2х+1<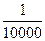

Содержание темы «Логарифмическая функция»

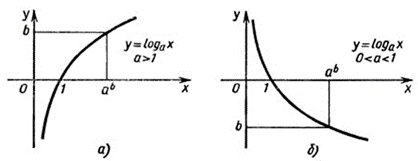
Определение логарифма, свойства логарифмов

Определение логарифма числа, основное логарифмическое тождество. Свойства логарифмов. Обозначение десятичного и натурального логарифма;

ознакомиться с таблицей Брадиса. Десятичные и натуральные логарифмы .

Логарифмическая функция и ее график

Вид логарифмической функции, её основные свойства. Построение графика логарифмической функции с данным основанием.

Логарифмические уравнения

Виды логарифмических уравнений, основные приёмы решения

логарифмических уравнений

Логарифмические неравенства

Виды логарифмических неравенств, основные приёмы решения

логарифмических неравенств

Основные сведения из теории

2.1. Основные свойства логарифма

Определение: Логарифмом числа х по основанию а, где а>0, а≠1, называется показатель степени, в которую надо возвести число а, чтобы получить число х.

Определение: Действие нахождения логарифма числа называют логарифмированием.

Обозначение: log_ах (логарифм числа х по основанию а)

а - основание логарифма

log_ах=в, то х=а^в

Основные свойства:

1) log_аа =1

2) log_а1=0

3) а ^logах=х (х>0,a>0, а≠1, основное логарифмическое тождество)

Теорема: Пусть а>0, а≠1, х>0, х₁>0, х₂>0, р- любое действительное число. Тогда справедливы формулы:

4) log_ах₁+ log_ах₂= log_а(х₁·х₂)

5) log_ах₁-log_ах₂= log_а( )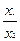

6) log_ах^р=р·log_ах

Логарифмическая функция,

Её свойства и график

Определение: Функцию у= log_ах, где а>0, а≠1, называют логарифмической функцией.

Свойство 1: Область определения логарифмической функции – множество всех положительных чисел.

Свойство 2: Множество значений логарифмической функции – множество всех R действительных чисел.

Свойство 3: Логарифмическая функция является возрастающей, если а>1, и убывающей если 0<a<1.
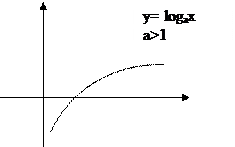
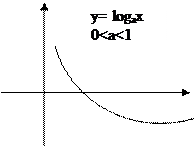