Опытные данные и подбор параметров линейной функции
Необходимое условие существования аппроксимирующих функций по методу трех выбранных точек.
| № | 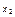 | 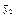 | Вид функции |
 (среднее арифметическое) (среднее арифметическое) |  (среднее арифметическое) (среднее арифметическое) | 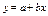 (линейная функция) (линейная функция) | |
 .(среднее геометрическое) .(среднее геометрическое) |  .(среднее геометрическое) .(среднее геометрическое) | 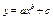 (степенная функция) (степенная функция) | |
 (среднее арифметическое) (среднее арифметическое) |  .(среднее геометрическое) .(среднее геометрическое) | 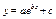 , (показательная функция) , (показательная функция) | |
 (среднее гармоническое) (среднее гармоническое) |  (среднее арифметическое) (среднее арифметическое) | 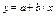 (гиперболическая функция) (гиперболическая функция) | |
 (среднее арифметическое) (среднее арифметическое) |  (среднее гармоническое) (среднее гармоническое) |  (дробно - линейная функция) (дробно - линейная функция) | |
 (среднее гармоническое) (среднее гармоническое) |  (среднее гармоническое) (среднее гармоническое) |  (дробно-рациональная функция) (дробно-рациональная функция) | |
 .(среднее геометрическое) .(среднее геометрическое) |  (среднее арифметическое) (среднее арифметическое) | 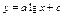 (логарифмическая функция) (логарифмическая функция) |
Для проверки пригодности той или иной аппроксимирующей опытные данные функции по методу трех выбранных точек рекомендуется использовать следующий алгоритм:
1. Выбираем из опытных данных крайние точки: начальную 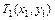 и конечную
и конечную 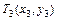 .
.
2. Вычисляем по формулам второго столбца таблицы 9 значения  для нескольких формул, которыми предполагается аппроксимировать опытные данные.
для нескольких формул, которыми предполагается аппроксимировать опытные данные.
3. Используя сглаженный график, построенный по опытным данным, определяем опытное значение  , соответствующее значению
, соответствующее значению  определенному по п.2.
определенному по п.2.
4. Вычисляем по формулам третьего столбца таблицы 9 значения  , соответствующие значениям
, соответствующие значениям  , для формул, которыми предполагается аппроксимировать опытные данные.
, для формул, которыми предполагается аппроксимировать опытные данные.
5. Вычисляем разность между опытным и вычисленным по п.4 значениями  .
.
6. Предпочтение отдается той формуле, для которой расхождение между опытным и вычисленным значением -  наименьшее.
наименьшее.
П р и м е р 9. Определить вид эмпирической формулы по методу трех выбранных точек для исходных данных, представленных в таблице 10.
Таблица 10
Исходные данные зависимости 
 | |||||
 | 1,343 | 1,360 | 1,370 | 1,377 | 1,381 |
Р е ш е н и е. Будем искать аппроксимирующую зависимость среди функций, представленных в таблице 9. Для этого берем две крайние точки  (1500;1,343) и
(1500;1,343) и  (3500;1,381). Вычисляем значения
(3500;1,381). Вычисляем значения  :
:
среднее арифметическое  = (1500 + 3500)/2 = 2500;
= (1500 + 3500)/2 = 2500;
среднее геометрическое  =
= 
 = 2291;
= 2291;
среднее гармоническое  =
=  = 2100.
= 2100.
По данным таблицы 10 строим график (рис. 10.)

По графику опытной зависимости (рис. 10) измеряем опытное значение функции  для найденных значений аргумента
для найденных значений аргумента  :
:
 = 2500,
= 2500,  = 1,370;
= 1,370;
 = 2291,
= 2291,  = 1,363;
= 1,363;
 = 2100,
= 2100,  = 1,362.
= 1,362.
Вычисляем значение  как:
как:
среднее арифметическое:  = (1,343 + 1,381)/2 = 1,3624;
= (1,343 + 1,381)/2 = 1,3624;
среднее геометрическое:  =
=  =
=  = 1,3622;
= 1,3622;
среднее гармоническое:  = 1, 631
= 1, 631
Результаты расчетов сводим в таблицу 11.
Таблица 11.
Определение коэффициентов эмпирической формулы (98)
Методом наименьших квадратов
 |  |  |  |  |
 | 0,075 0,225 0,400 0,600 0,750  |  | 0,005625 0,050625 0,16 0,56 0,5625  | 5,775 16,425 26,0 34,8 39,0  |
Используя данные таблицы 17 и выражения (88), получим систему нормальных уравнений в виде
 ;
;
 ,
,
решая которые находим коэффициенты 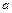 и
и 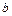
 ;
;
 .
.
Следовательно, искомая эмпирическая формула будет иметь вид
 . (99)
. (99)
Оценка точности полученной формулы приведена в таблице 18.
Таблица 18
Опытные данные и подбор параметров линейной функции
 | |||||
| Опытные данные |  | ||||
 | 3,0 | 5,9 | 7,0 | 9,6 | |
| Расчет (графический метод) |  | 3,24 | 5,48 | 7,72 | 9,96 |
 | -0,24 | 0,42 | -0,72 | -0,36 | |
| Расчет (метод парных точек) |  | 3,53 | 5,45 | 7,83 | 9,30 |
 | -0,53 | 0,45 | -0,38 | 0,3 |
отрезку  , отсекаемому на оси ординат при нулевом значении аргумента.
, отсекаемому на оси ординат при нулевом значении аргумента. 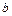 - определяется по выражению (12). В нашем случае
- определяется по выражению (12). В нашем случае 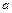 = 1,0,
= 1,0, 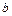 = (10 – 1,0)/8 = 1,12.
= (10 – 1,0)/8 = 1,12.
Принимаем аппроксимирующую функцию в виде
 (18)
(18)
Соответствие подобранной эмпирической функции (18) опытным значениям проверяем по выражению (9), для чего определяются значения  (таблица 1).
(таблица 1).
 .
.
|

Рис. 5. Вид эмпирической функции
Подбор параметров аппроксимирующего уравнения можно произвести по методу парных точек. Для этого берем две пары точек 1-3 и 2-4. Параметры 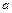 и
и 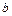 линейного уравнения определяем по (17)
линейного уравнения определяем по (17)
Для первой пары точек
 ;
;  .
.
Для второй пары точек
 ;
;  .
.
Среднее значение параметров равно
 ;
;  .
.
Эмпирическая формула имеет вид
 . (20)
. (20)
Подбор параметров аппроксимирующей функции аналитическим методом парных точек не зависит от воли исследователя, проведенная им сглаживающая линия лишь указывает на вид аппроксимирующей функции, а ее параметры определяются по опытным данным.
Данные для оценки степени совпадения расчетных значений с опытными приведены в таблице 1.

Метод парных точек, обычно, дает более точное значение параметров эмпирической формулы по сравнению с графическим методом. Дело в том, что вид функции (наклон прямой) при графическим методе определения параметров полностью зависит от того, как исследователь проведет сглаживающую линию, на сколько она будет соответствовать опытным точкам.
Вопросы для контроля.
1. Какого правила следует придерживаться при подборе аппроксимирующей функции?
2. Какими методами можно определить параметры линейной аппроксимирующей функции?
3. Изложите суть графического метода определения параметров линейного уравнения.
4. В каких случаях удобнее использовать метод двух точек для определения параметров линейного уравнения?
5. Какие преимущества дает метод парных точек подбора параметров линейного уравнения по сравнению с методом двух точек?
4. ЛИНЕАЛИЗАЦИЯ ГРАФИКОВ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ
Простейшим аппроксимирующим выражением является уравнение прямой линии. Если опытные данные не укладываются вблизи прямой линии, необходимо провести линеализацию сглаживающей кривой. Суть метода сводится к следующему. Для преобразования некоторой кривой  в прямую линию вводят новые переменные
в прямую линию вводят новые переменные  и
и  , которые должны быть связаны между собой линейной зависимостью
, которые должны быть связаны между собой линейной зависимостью
 , (21)
, (21)
Функции преобразования координат  и
и  зависят от вида выбранной аппроксимирующей функции.
зависят от вида выбранной аппроксимирующей функции.
Если экспериментальный график  проходит через начало координат и имеет вид, изображенный на рис. 2в, то экспериментальные данные описываются степенной функцией вида
проходит через начало координат и имеет вид, изображенный на рис. 2в, то экспериментальные данные описываются степенной функцией вида
 (22)
(22)
Прологарифмировав (22) получим
 . (23)
. (23)
Заменяя в (23)  ,
,  ,
,  ,
,  , получим линейную функцию
, получим линейную функцию
 (24)
(24)
Таким образом степенная функция (22) превращается в прямую линию в логарифмической системе координат  ,
,  . Параметры
. Параметры 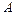 и
и 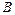 функции (24) определяются известными методами.
функции (24) определяются известными методами.
Переход к параметрам степенной функции (22) делается следующим образом:
 , отсюда
, отсюда  ,
,  . (25)
. (25)
П р и м е р 3. Подобрать эмпирическую формулу по исходным данным, представленным в таблице 2.
Таблица 2

