И построения структуры АСОИУ

Пусть G – построенный информационно-логический граф, а G^* - граф, называемый конденсацией графа G, который определяется следующим образом: каждая его вершина 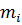соответствует множеству вершин некоторой сильной компоненте 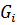графа G, то есть 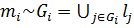(разным сильным компонентам из графа G отвечают разные вершины в конденсации G^*); дуга 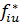существует в конденсации G^* тогда и только тогда, когда в графе G имеется такая дуга 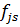, что вершина 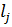принадлежит сильной компоненте 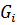, соответствующей вершине 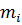в конденсации G^*, а вершина 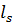принадлежит сильной компоненте 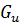, соответствующей вершине 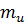в конденсации G^*, то есть справедливы следующие соотношения: 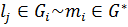, а .

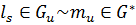Сильными компонентами графа 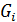будем считать максимальные подграфы графа G, обладающие заданным свойством. Поскольку в данном случае в качестве такого свойства выступает сильная связность вершин графа G, его сильные компоненты будут представлять собой подмножества (порожденные подграфы) взаимно связных вершин.

Требуется найти его сильные компоненты и построить конденсацию графа G, то есть построить граф G^*.

Эта процедура реализуется при использовании матриц достижимости R_G и контрдостижимости Q_G графа G.

Матрица достижимости R_G=||r_js|| определяется следующим образом:

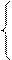1, если вершина ℓ_s достижима из вершины ℓ_j (т.е. ℓ_j→ℓ_s)

r_js=

0, в противном случае.

Вершина ℓ_s считается достижимой из вершины ℓ_j, если существует путь от вершины ℓ_j к вершине ℓ_s.

Полагают, что все диагональные элементы матрицы R_G равны 1, т.к. каждая вершина достижима из самой себя путем длиной 0. В качестве алгоритма построения матрицы достижимости R_G можно предложить следующий:

Вход: Матрица A_G смежности графа G, состоящая из строк A₁, A₂,…, A_j,…, A_k; A_j=(a_j1,…, a_js,…, a_jk)

Выход: Матрица достижимости R_G, состоящая из строк R₁, R₂,..., R_j,…, R_k, где

R_j=(r_j1,…, r_js,…, r_jk)

Алгоритм запишем в виде, использующем так называемый псевдоалгол:

Начало

1. для j от 1 до k шаг 1 цикл А

2. сформировать множество S индексов s таких, что a_js=1;

3. R_j := A_j ; k:=0;

4. пока S≠0 цикл В

5. выбрать sєS;

6. R_j:=R_j 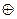A_s;

7. S:=S\{s};

8. K:=K 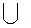{s};

9. Сформировать множество S_s индексов r таких, что a_sr=1;

10. S:=S 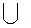(S_s\K);

11. конец цикла В;

12. возврат R_j;

13. конец цикла А;

Конец

Матрица контрдостижимости Q_G=║q_js║ определяется следующим образом:

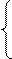1, если из вершины ℓ_s графа G достижима вершина ℓ_j (т.е. ℓ_j←ℓ_s)

q_js=

0, в противном случае.

При этом q_js=1, если j=s. Очевидно, что матрица Q_G есть транспонированная матрица R_G.

На следующем этапе алгоритма выполняется поэлементное умножение матриц R_G и Q_G графа G, в результате чего получаем матрицу (R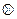_G Q_G).

При этом строка ℓ_j матрицы R_G 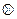Q_G содержит единицы только в тех столбцах ℓ_s , для которых выполняется условие: вершины ℓ_j и ℓ_s взаимно достижимы. В других местах строки стоят нули. Таким образом, две вершины графа G находятся в одной и той же сильной компоненте тогда, когда соответствующие им строки (или столбцы) в матрице R_G 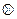Q_G идентичны.

Следующий шаг алгоритма – преобразование матрицы (R_G 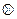Q_G )путем транспонирования ее строк и столбцов в блочно-диагональную матрицу 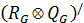, каждая из диагональных подматриц (блоков) которой соответствует сильной компоненте графа G и содержит только единичные элементы, поскольку вершины, которым отвечают строки, имеющие единицу в столбце ℓ_s, образуют множество вершин сильной компоненты, содержащей вершину ℓ_s. Все остальные блоки данной матрицы имеют нули.

Графическое представление полученной диагональной матрицы представляет собой граф искомой структуры, рассматриваемой АСОИУ.

Для инфологического графа G , представленного на рис. 1, его конденсация, то есть граф G^* , полученный путем применением рассмотренного алгоритма, представлен на рис. 2.

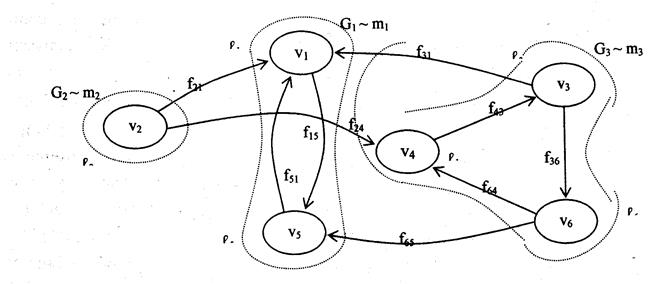
Рис. 1. Пример инфологического графа АСОИУ

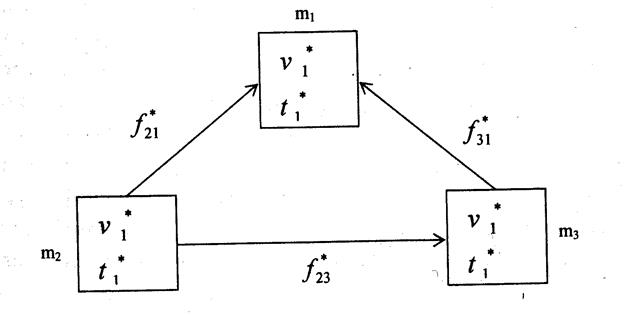
Рис. 2. Граф G^* как структура АСОИУ