Параметры распределения вероятности и выборки

Данные параметры разделяют на характеристики расположения и рассеяния.

Основной характеристикой расположения является среднее значение, которое определяется как среднее арифметическое ( 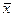) и находится по формуле:

,

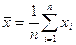где п - число наблюдений;

х - текущее значение данного наблюдения.

Основной мерой рассеяния выборочных значений является дисперсия ( 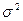), характеризующая степень разброса количественных измерений индивидуальных значений выборки относительно среднего значения для этой выборки. Дисперсия определяется по одной из двух следующих формул:

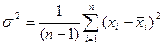или

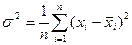
Вторая из них используется для достаточно больших п (п>10).

Среднее квадратичное отклонение ( 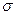) определяется по формулам:

или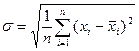

Математическое ожидание (т) представляет собой наиболее вероятное ожидаемое значение. этой величины. Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных ее значений (х) на их вероятности (р):

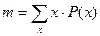
Размах — величина, равная разнице между наибольшим и наименьшим значением выборки :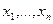

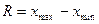
2. Биномиальное распределение

Если партия из большого числа изделий N содержит некоторую долю дефектных изделий р, некоторую долю годных изделий q, то вероятность получения дефектного изделия в отдельном испытании составит р, а вероятность годного изделия будет равна q=1-p.

При применении выборочного метода контроля вероятность того, что в выборке объема n число дефектных изделий в точности равно 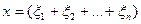определяется по формуле:

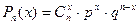
где

р - вероятность появления брака,

q — вероятность появления годного изделия,

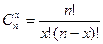- число возможных групп по х элементов в каждой, которые можно составить из п различных элементов, пренебрегая порядком элементов в каждой группе.

При использовании биномиального закона на практике определяют кумулятивную вероятность, т.е. накопленную вероятность F(п,х). Данная величина оценивает накопление дефектных изделий в выборке и находится по формуле:

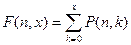
где k - число дефектных изделий, для которых выполняется расчет.

Биномиальный закон применяют для: - определения выборки, позволяющей осуществить приемку по альтернативным признакам (число бракованных изделий); - управления процессом «р» (процент брака).

Контрольное задание № 1

По нижеприведенным данным (таблица 2.1) оценить вероятность появления бракованных изделий и кумулятивную вероятность для данной выборки. Результаты расчетов занести в таблицу 2.2. Построить графики плотности вероятности и кумулятивной вероятности, пример которых показан на рис.2.1.

Таблица 2.1

№ варианта	Число дефектных изделий х, шт	Вероятность получения дефектных изделий р	Вероятность получения годных изделий q	Объем выборки п
	0-10	0,05	0,95
	0-9	0,14	0,86
	0-8	0,03	0,97
	0-7	0,2	0,8
	0-6	0,06	0.94
	0-5	0,07	0,93
	0-11	0,1	0,9
	0-12	0,09	0,91
	0-13	0,17	0,83
	0-14	0,08	0,92

Таблица 2.2 Оценки вероятности обнаружения дефектных изделий

Число дефектных изделий х, шт	Вероятность Рn(х)	Кумулятивная вероятность F(x, n)
…
x

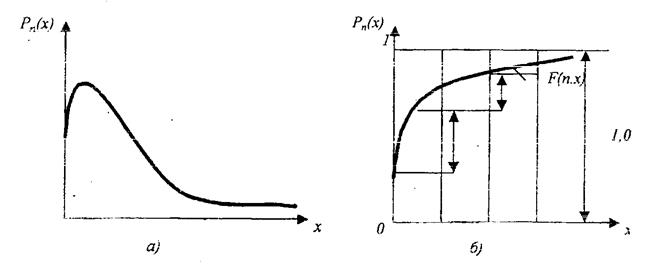
Рис. 2.1. Графики плотности вероятности (а) и кумулятивной вероятности (б)

Распределение Пуассона

Распределение Пуассона относится к тем случаям, когда число случайных событий происходит на определенной длине площади, объеме или времени. Здесь основным определяющим параметром распределения является среднее число событий т. Распределение вероятности для х имеет следующий вид:

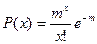, где m=np.

Распределение Пуассона аппроксимирует биномиальные распределения в пределе, когд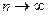а , а 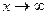так, что среднее пр = т - const.

Таким образом, распределение Пуассона является предельным для биномиального распределения, когда вероятность ( 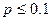) мала, число событий велико, а математическое ожидание появления дефектных изделий является ограниченным числом.

Это распределение иногда называют законом распределения редких событий.

Контрольное задание № 2

По данным таблицы 3.1 оценить вероятность появления бракованных изделий и кумулятивную вероятность для данной выборки. Результаты расчетов занести в таблицу 2.2. Построить графики плотности вероятности и кумулятивной вероятности. Сделать выводы.

Таблица 3.1

№ варианта	Число дефектных изделий х, шт	Вероятность получения дефектных изделий p	Вероятность получения годных изделий q	Объем выборки п
1		3	4	5
	0-10	0,005	0,995
	0-9	0,004	0,996
	0-8	0,003	0,997
	0-7	0,002	0,998
	0-6	0,02	0,'98
	0-5	0,007	0,993
	0-11	0,01	0,99
	0-12	0,02	0,98
	0-13	0,03 | 0,97	0,97
	0-14	0,015 1 0,985	0,985