К расчетно-графической работе

Примеры записи решений заданий

К расчетно-графической работе

Пример 1

Задание:По данным выборки:

1. Составить дискретный вариационный ряд.

2. Построить полигон.

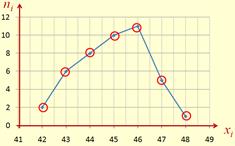
3. Найти средние характеристики:

а) среднее выборочное ;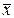

б) моду ;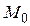

в) медиану .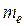

4. Найти характеристики вариации:

а) размах вариации ;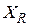

б) дисперсию D;

в) среднее квадратическое отклонение s;

г) коэффициент вариации V;

д) ошибку выборочного среднего .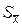

5. Сделать вывод.

Исходные данные:

Число отжиманий в упоре лежа

43 46 45 43 44 45 47 43 44 46

45 44 42 45 47 44 46 46 46 43

46 43 44 47 45 46 42 44 44 46

47 45 46 46 48 45 45 43 45 47

46 44 45

Этапы выполнения:

Cоставим дискретный вариационный ряд.

Все варианты расположим в порядке возрастания в первой строке таблицы, а частоту, с которой они встречаются в данной выборке во второй строке.

xi
ni

Объем выборки n=43.

Построим полигон.

Для построения полигона на оси OX отложим значения вариант x_i, а на оси OY – значения частот n_i.

Вычислим средние характеристики.

а) Определим среднее выборочное :

,

Вычисления оформим в виде таблицы:

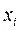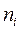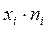		å=1933

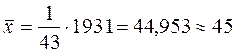
б) Определим моду :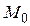

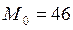
в) Определить медиану :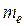

Выборку сначала необходимо проранжировать:

42 42 43 43 43 43 43 43 44 44

44 44 44 44 44 44 45 45 45 45

45 45 45 45 45 45 46 46 46 46

46 46 46 46 46 46 46 47 47 47

47 47 48

Объем выборки n=43 является нечетным числом, следовательно 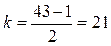, значит, 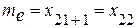, то есть 22-ой по счету вариант в ранжированном ряду и будет медианой: .

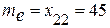Вычислим характеристики вариации.

а) Определим размах вариации :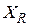

,

.

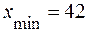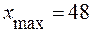
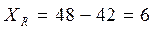б) Определим дисперсию D:

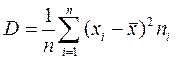, где

Вычисления оформим в виде таблицы:

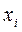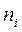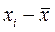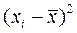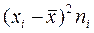		-3
		-2
		-1
				å=90

.

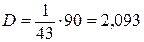в) Определим среднее квадратическое отклонение s:

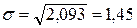(≈1).

г) Определим коэффициент вариации V:

.

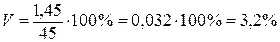д) Определим ошибку выборочного среднего :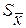

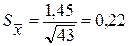(≈0).

5. Вывод. По данным числа отжиманий в упоре лежа 43 испытуемых средний результат составил 45 раз ± 0 раз. Степень рассеяния данных выборки от среднего результата составляет 1 отжимание. Чаще всего встречаемый результат в группе – 46 отжиманий. Одна половина спортсменов показала результаты лучше 45 отжиманий, а другая половина хуже. Отклонение результатов числа отжиманий в упоре лежа внутри группы равно 6 отжиманиям. Результаты исследования имеют малую варьируемость, что говорит об однородности выборки, то есть средний результат типичен для изучаемого признака.

Пример 2

Задание: По данным выборки:

1. Составить интервальный вариационный ряд.

2. Начертить гистограмму.

3. Найти средние характеристики:

а) среднюю выборочную ;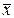

б) моду ;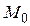

в) медиану .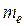

4. Найти характеристики вариации:

а) размах вариации ;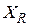

б) дисперсию D;

в) среднее квадратическое отклонение s;

г) коэффициент вариации V;

д) ошибку выборочного среднего .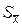

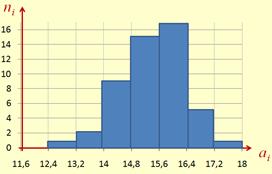
Исходные данные: Бег на 100 м (юноши 9 классов).

16,2 15,5 14,3 16,6 15,8 15,4 14,5 14,8 16,1 15,8

15,3 16,0 13,7 16,1 16,2 15,3 15,5 14,8 14,3 16,2

15,3 15,8 14,2 15,8 14,2 15,4 14,7 12,8 16,9 15,0

16,8 16,0 14,6 15,6 16,1 17,8 15,6 15,0 15,6 15,0

16,2 15,5 13,6 16,4 15,2 15,9 15,0 14,2 16,4 14,2

Этапы выполнения:

Построим гистограмму.

Пример 3

Задание:

1. Проверить гипотезу о нормальном распределении признака в генеральной совокупностис помощью критерия согласия Пирсона c² для уровня значимости a=0,05.

2. Построить нормальную кривую.

3. Сделать вывод.

Исходные данные: Бег 100м: 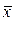=15,4, s = 0,9, h =0,8, n=50.

xi	12,8	13,6	14,4	15,2	16,0	16,8	17,6
ni

Этапы выполнения:

Построим нормальную кривую.

Для построения нормальной кривой на оси OX откладывают значения x_i, а на оси OY – соответствующие значения выравнивающих частот n_i^’.

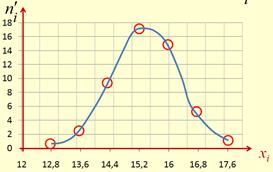
3. Вывод.Выдвинутая гипотеза о нормальном распределении результатов в беге на 100м у данных спортсменов принимается на уровне значимости 0,05, так как расчетное значение критерия согласия c₀²=2,56 меньше критического значения c2=9,49. Средний результат в беге на 100м в 95% случаев у обследуемых спортсменов находится в пределах от 15,2с до 15,6с, а дисперсия с вероятностью 0,95 не выйдет за границы 0,49 – 1,13.

Пример 4

Задание:

1. Сравнить по методу Фишера рассеивание показателей в контрольной и экспериментальной группах на уровне значимости a=0,05.

2. Сделать вывод.

Исходные данные: Гребля на каноэ 500м.

xэ,мин	2,00	1,69	2,12	2,10	2,15	1,78	2,30	1,80
xк,мин	2,20	2,25	2,40	2,20	2,05	2,50	2,40	2,10

Этапы выполнения:

1. Сравним по методу Фишера рассеивание показателей в контрольной и экспериментальной группах на уровне значимости a=0,05.

1). Выдвигаем нулевую гипотезу.

H₀: (D_э=D_к) – дисперсии результатов гребли на каноэ 500м в экспериментальной и контрольной группах не отличаются значимо.

2). Рассчитываем выборочные дисперсии результатов измерений.

Результаты вычислений оформим в виде таблицы:

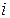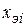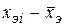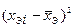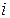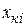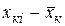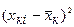	2,00	-0,12	0,01			2,20	-0,06	0,00
	1,69	-0,43	0,18			2,25	-0,01	0,00
	2,12					2,40	0,14	0,02
	2,10	-0,02	0,00			2,20	-0,06	0,00
	2,15	0,03	0,00			2,05	-0,21	0,04
	2,78	0,66	0,44			2,50	0,24	0,06
	2,30	0,18	0,03			2,40	0,14	0,02
	1,80	-0,32	0,10			2,10	-0,16	0,03
	S=16,94		S=0,76			S=18,10		S=0,17

, ,

,.

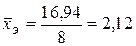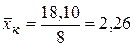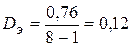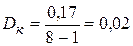3). Вычисляем расчетное значение F-критерия (Фишера).

Так как D_э>D_к Þ .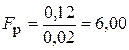

4). Находим число степеней свободы.

n_э=8-1=7, n_к=8-1=7.

5). По таблице (см. приложение 4) находим критическое значение F-критерия для уровня значимости a=0,05 и числа степеней свободы n_э=7, n_к=7:F(0,05;7;7)=3,8.

6). Проверяем гипотезу: сравниваем расчетное значение критерия F_р с табличным значением F (то есть, оцениваем достоверность различий выборочных совокупностей).

F_р > F (6,00>3,8)

Вывод.Таким образом, выдвинутая гипотеза отвергается на уровне значимости a=0,05, то есть с вероятностью 0,95 различие дисперсий существенно, что позволяет говорить о принадлежности дисперсий к разным генеральным совокупностям.

Пример 5

Задание:

1. Установить по методу Стъюдента (для несвязанных выборок) достоверность различия результатов в двух группах, занимающихся по различной методике (a=0,01).

2. Сделать вывод.

Исходные данные:Бег 60м.

x1,м	8,2	7,8	8,2	8,3	7,6	8,4	7,7	8,3
x2,м	9,2	8,9	8,6	9,0	7,9	8,7	8,6	8,8	9,1

Этапы выполнения:

1. Установим по методу Стъюдента (для несвязанных выборок) достоверность различия результатов в двух группах, занимающихся по различной методике (a=0,01).

1). Выдвигаем нулевую гипотезу.

H₀: ( 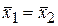) – средние выборочные значения результатов бега на 100м в экспериментальной и контрольной группах не отличаются значимо.

2). Рассчитываем значения выборочных характеристик , , , .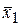

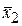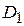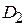Результаты вычислений оформим в виде таблицы:

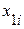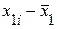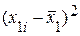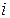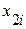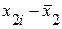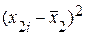	8,2	0,1	0,01			9,2	0,4	0,16
	7,8	-0,3	0,09			8,9	0,1	0,01
	8,2	0,1	0,01			8,6	-0,2	0,04
	8,3	0,2	0,04			9,0	0,2	0,04
	7,6	-0,5	0,25			7,9	-0,9	0,81
	8,4	0,3	0,09			8,7	-0,1	0,01
	7,7	-0,4	0,16			8,6	-0,2	0,04
	8,3	0,2	0,04			8,8
	S=64,5		S=0,69			9,1	0,3	0,09
						S=78,8		S=1,2

, ,

,.

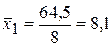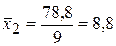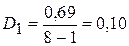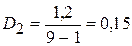3). Вычисляем расчетное значение t-критерия Стъюдента.

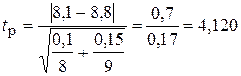
4). Находим число степеней свободы.

n=8+9-2=15.

5). По таблице (см. приложение 5) находим критическое значение t-критерия Стъюдента для уровня значимости a=0,01 и числа степеней свободы n=15:t(0,01;15)=2,947.

6). Проверяем гипотезу: сравниваем расчетное значение критерия t_р с табличным значением t (то есть, оцениваем достоверность различий выборочных совокупностей).

t_р>t (4,120>2,947)

Вывод.Таким образом, выдвинутая гипотеза отвергается на уровне значимости a=0,01, то есть с вероятностью 0,99 по средним результатам группы существенно отличаются, что позволяет говорить об эффективности проводимой во второй группе методике.

Пример 6

Задание: Определить по методу Стъюдента (для связанных выборок) изменилось ли состояние спортсменов по результатам, показанным ими с разрывом в 10 дней на уровне значимости a=0,001.

Исходные данные: Число отжиманий в упоре лежа.

x1, раз
x2, раз

Этапы выполнения:

Выдвигаем нулевую гипотезу.

H₀: ( 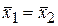) – средние выборочные результатов в отжиманиях в упоре лежа одинаковы, то есть значимо не отличаются.

2. Рассчитываем основные характеристики , :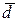

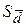Результаты вычислений оформим в виде таблицы:

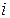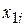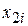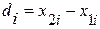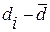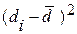				4,3	18,49
				4,3	18,49
				-2,7	7,29
				0,3	0,09
				-0,7	0,49
				-0,7	0,49
				-1,7	2,89
				-3,7	13,69
				0,3	0,09
			S=33		S=62,01

, , .

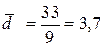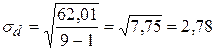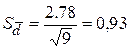Пример 7

Задание:

1. Представить результаты измерений в графической форме (построить корреляционное поле).

2. Установить тесноту взаимосвязи двух исследуемых признаков, применяя метод Бравэ-Пирсона.

3. Оценить достоверность коэффициента корреляции на уровне значимости a=0,05 .

4. Составить уравнение регрессии y(x) и построить линию регрессии y(x).

5. Сделать вывод.

Исходные данные: Десятиборцы, x_i –результаты в прыжках в длину (м),

y_i – результаты в беге на 100 м (с).

xi,м	7,62	7,37	6,93	7,40	7,03	7,15	7,13
yi, с	10,8	10,8	11,1	11,1	11,3	11,4	11,1

Этапы выполнения:

Пример 8

Задание:

1.Определить тесноту взаимосвязи между результатами методом Спирмена.

2. Оценить достоверность коэффициента корреляции на уровне значимости a=0,05.

3. Сделать вывод.

Исходные данные: Легкоатлеты,

x_i –результаты в беге на 100 м,

y_i – место, занятое в соревнованиях по тройному прыжку.

xi, с	10,7	10,6	10,7	10,5	10,9	10,4	10,3	10,7	10,7
yi

Этапы выполнения:

Примеры записи решений заданий

к расчетно-графической работе

Пример 1

Задание:По данным выборки:

1. Составить дискретный вариационный ряд.

2. Построить полигон.

3. Найти средние характеристики:

а) среднее выборочное ;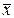

б) моду ;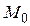

в) медиану .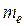

4. Найти характеристики вариации:

а) размах вариации ;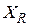

б) дисперсию D;

в) среднее квадратическое отклонение s;

г) коэффициент вариации V;

д) ошибку выборочного среднего .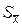

5. Сделать вывод.

Исходные данные:

Число отжиманий в упоре лежа

43 46 45 43 44 45 47 43 44 46

45 44 42 45 47 44 46 46 46 43

46 43 44 47 45 46 42 44 44 46

47 45 46 46 48 45 45 43 45 47

46 44 45

Этапы выполнения: