Вычисление ошибок основных статистических показателей

Между значениями статистических показателей выборочной совокупности и действительными значениями этих показателей в генеральной совокупности всегда будут некоторые расхождения, которые являются случайными ошибками выборки и называются основными ошибками того или иного статистического показателя. Ошибки возникают вследствие неполной репрезентативности (представительности) выборочной совокупности и свойственны только выборочному методу исследования. Они связаны с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность. Величина ошибок зависит от степени изменчивости изучаемого признака и от объема выборки. Ошибки статистических показателей выражают в тех же единицах измерения, что и варьирующий признак и приписывают к соответствующим показателям со знаками .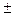

Основные ошибки статистических показателей вычисляют по формулам:

- ошибка выборочной средней

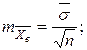(7)

- ошибка среднего квадратичного отклонения

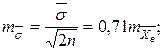(8)

- ошибка коэффициента вариации

m_v= 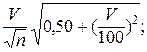(9)

- ошибка коэффициента асимметрии

m_A= 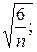(10)

- ошибка эксцесса

m_Е= 2m_A (11)

Ошибки вычисляются с той же точностью, с которой вычислены соответствующие статистические показатели, но с количеством значащих цифр не менее двух.

Кроме абсолютной ошибки выборочной средней (7), часто требуется определить относительную ошибку выборочной средней:

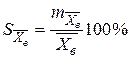(12)

Она показывает, на сколько процентов можно ошибиться, если утверждать, что генеральная средняя равна полученной выборочной средней.

Определение достоверности (надежности) выборочных статистических показателей

После вычисления того или иного статистического показателя требуется проверить степень его достоверности или надежности. Для этой цели вычисляют показатель достоверности (надежности), который представляет собой отношение величины оцениваемого статистического показателя к его ошибке:

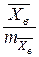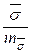t = 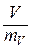; t = ; t 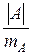= ; t= ; t= 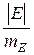. (13)

Принято оценивать достоверность статистических показателей на трех уровнях значимости: с вероятностью 95% (5%-ный уровень значимости), 99% (1%-ный уровень значимости) и 99,9% (0,1%-ный уровень значимости). В обычных исследованиях достаточно использовать 5%-ный уровень значимости. Для определения достоверности статистического показателя на заданном уровне значимости 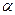полученную величину t сравнивают со стандартной величиной t(k, 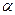), которую определяют на нужном уровне значимости 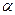по таблице критерия t Стьюдента (Приложение 1) в зависимости от числа степеней свободы k=n-1, где n – число наблюдений (объем выборки). Если t 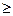t(k, 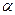), то значение показателя является надежным, достоверным и им можно пользоваться для различных сопоставлений и выводов. Если же t < t(k, 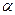), то данный показатель оказывается ненадежным, величина его не достоверна и является лишь в той или иной мере вероятной.