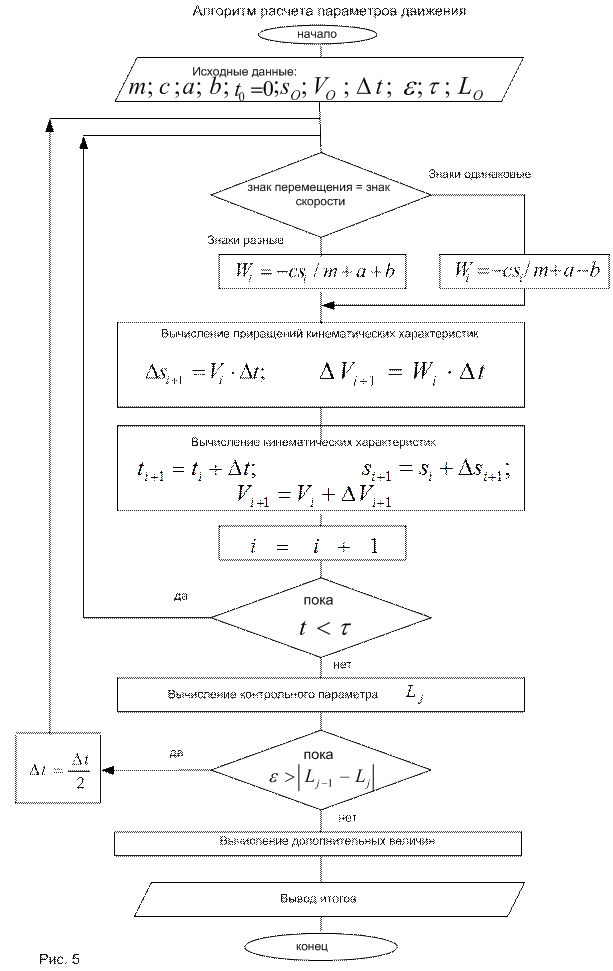
Получение рекуррентных зависимостей для моделирования процесса движения

Перепишем дифференциальное уравнение второго порядка для движения груза механической системы в виде двух дифференциальных уравнений первого порядка, опустив индекс «1»:

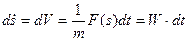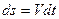; (23)

здесь 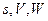- координата, скорость и ускорение груза, 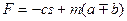- выражение, отражающее действие внешних сил, действующих на тела механической системы.

Уравнения (23) определяют приращения 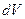и 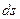величин 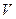и 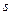за промежуток времени 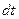, т.е. характеризует изменение во времени параметров состояния движения (положение и скорость) груза под действием усилий, приложенных к телам механической системы. Естественно, что начальные условия 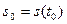и 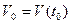должны быть заданы.

Заменив в (23) бесконечно малые приращения 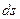, 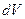и 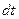на малые, но конечные приращения 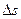, 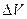и 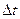, получим соотношения

;

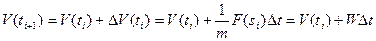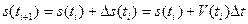; (24)

.

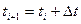Зависимости (24) носят рекуррентный характер и позволяют последовательно находить (разумеется, приближенно) положение, скорость и ускорение точки, идя от ее начального положения.

Точность решения повышается с уменьшением шага 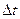по времени. Оценку погрешности рекомендуется выполнить методом двойного пересчета по формуле Рунге

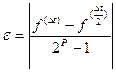
, где 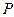- порядок метода (для семейства методов Эйлера ).

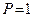Расчет целесообразно повторять с уменьшением шага до тех пор, пока различие результатов двух последовательных расчетов не окажется в пределах требуемой точности.

Для повышения точности расчета преподавателем может быть задано использование иных методов из семейства методов Эйлера (усовершенствованный метод, метод Эйлера Коши, с итерационной обработкой). Рекуррентные зависимости в этом случае необходимо получить самостоятельно (см, например, [2]).

Описание алгоритма расчета

Исходные данные задачи:

- предварительно вычисленные величины: ;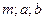

- заданные величины: .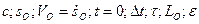

Здесь 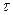- время длительности процесса, 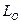- начальное значение контрольного параметр расчета (например – наибольшее отклонение груза от начала отсчета), а 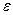- величина погрешности при расчете контрольного параметра.

Сформулируем алгоритм расчета параметров движения (положение, скорость и ускорение) для груза механической системы.

1. Производится сравнение знаков перемещения и скорости для момента времени 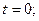выбирается вариант вычисления величины .

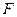2. По заданным начальным условиям вычисляется значение ускорения в начальный момент времени как .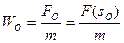

3. Вычисляются значения приращений перемещения и скорости груза как

.

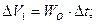
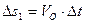4. Вычисляются значения перемещения и скорости груза в момент времени 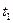как

.

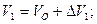
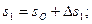
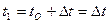5. Вычисленные величины сохраняются в созданной базе данных .

6. Сравнивается вычисленное значение времени 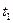с заданным временем расчета процесса .

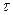Если 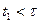расчет продолжается возвратом к первому пункту алгоритма.

При 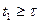происходит переход к анализу погрешности вычислений.

7. Вычисляется (или присваивается) значение контрольного параметра 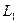. Заданное значение погрешности 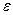позволяет выполнить сравнение величин 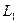и 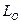. Если отличие не превышает величины 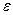, расчет кинематических характеристик заканчивается и происходит переход к расчету дополнительных величин. В противном случае расчет повторяется с уменьшенным вдвое шагом интегрирования по времени ( ).

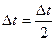8. Вычисляются дополнительные величины, указанные преподавателем (например, реакции внутренних и внешних связей и т.п.). Значения величин сохраняются в созданной базе данных.

Замечание: выполнение такого расчета теперь не вызывает затруднений – для этого в дифференциальные уравнения движения тел механической системы следует подставить найденные значения перемещения, скорости и ускорения для любого момента времени и решить систему алгебраических уравнений относительно неизвестных величин.

9. Сохраненные в базах данных величины (см. п.п. 5 и 8) выводятся на печать.