Теорема об изменении кинетической энергии механической системы
2.4.1. Кинетическая энергия механической системы.Кинетической энергией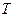 
материальной точки массы 
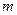, движущейся со скоростью 
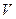, называют величину
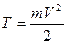. (6)
Кинетической энергией механической системы называют сумму кинетических энергий включенных в эту систему материальных точек:
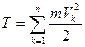. (7)
В тех случаях, когда масса системы распределена непрерывно, суммирование в выражении (7) заменяют интегрированием по области распределения.
Связь между значениями кинетической энергии механической системы в двух системах отсчета, одна из которых неподвижна, а другая движется поступательно со скоростью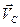 
, где точка С – центр масс механической системы, дает теорема Кенига:
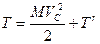. (8)
Здесь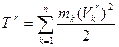 
- кинетическая энергия механической системы в подвижной системе координат.
Использование выражений (6, 7, 8) позволяет записать формулы для вычисления кинетической энергии твердого тела:
- при поступательном движении тела массой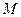 
со скоростью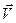 
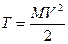; (9)
- при вращении с угловой скоростью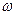 
вокруг неподвижной оси 
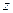тела с моментом инерции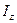 
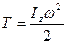; (10)
при плоскопараллельном движении твердого тела с угловой скоростью 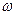при значении центрального момента инерции 
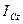относительно оси, перпендикулярной плоскости движения, и значении 
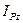момента инерции относительно мгновенной оси вращения
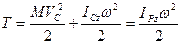. (11)
2.4.2. Энергетические характеристики. К энергетическим характеристикам силы относят ее мощность, работу и потенциальную энергию.
Мощностью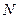 
силы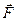 
, точка приложения которой движется со скоростью 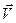, называют величину
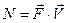. (12)
Работа силы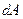 
на элементарном интервале времени 
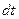и соответствующем этому промежутку времени элементарному смещению 
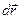точки приложения определяется по правилу
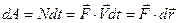. (13)
Работой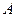 
силы на конечном интервале времени [0; 
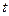] и соответствующем изменении радиуса – вектора точки приложения этой силы от 
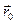до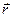 
называют величину
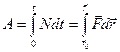. (14)
Работа момента пары сил вычисляется аналогично.
Потенциальная энергия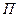 
определена только в тех случаях, когда выражение (13) представляет собой полный дифференциал :
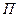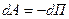. (15)
При выполнении условия (15) говорят, что сила потенциальна. Соотношения, связывающие проекции силы на оси выбранной координатной системы с функцией :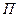
; 
; 
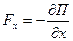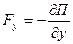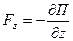. (16)
Если точка приложения силы переместилась из положения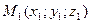 
в положение 
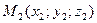, то путем интегрирования (15) можно получить
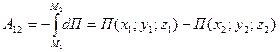. (17)
Замечание: потенциальная энергия определена с точностью до постоянного слагаемого; отмеченная особенность позволяет полагать потенциальную энергию равной нулю в выбираемой нами точке (например, в начале координат).
В том случае, когда для совокупности сил, действующих на механическую систему, можно записать выражение потенциальной энергии 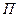, механическую систему называют консервативной. Такие механические системы обладают важными особенностями – работа действующих сил не зависит от вида траектории и закона движения по ней; работа при движении по замкнутому контуру равна нулю.
Условия, при выполнении которых существует функция :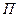
; 
; 
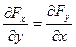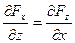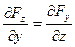. (18)
2.4.3. Теорема об изменении кинетической энергии.Запись теоремы об изменении кинетической энергии механической системы в дифференциальной форме:
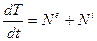. (19)
- производная по времени от кинетической энергии механической системы равна мощности внешних и внутренних сил.
Интегральная форма записи теоремы об изменении кинетической энергии
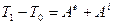, (20)
где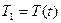 
; 
; 
; 
.
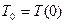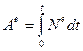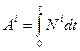В частном случае, когда для совокупности внешних и внутренних сил системы можно записать выражение потенциальной энергии, выполняется закон сохранения полной механической энергии
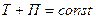, (21)
а сама система оказывается консервативной.
ПРИМЕР 3. Для механической системы, изображенной на рис.2, получить дифференциальное уравнение движения груза.
РЕШЕНИЕ. Воспользуемся теоремой об изменении кинетической энергии в дифференциальной форме (19). Мысленно освободимся от связей, приложив к телам механической системы соответствующие реакции (см.рис.2). Замечание: силы, приложенные в неподвижном центе масс соосного блока не изображены, так как их мощность равна нулю.
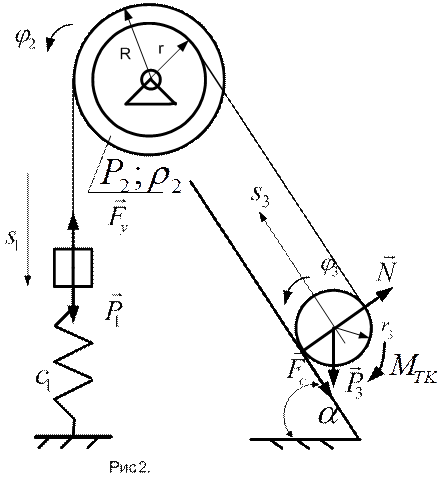
Составим выражение для кинетической энергии механической системы:
.
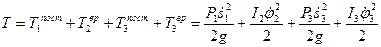Воспользуемся уравнениями кинематических связей для выражения скоростей движения тел механической системы через скорость движения груза:
; 
; 
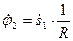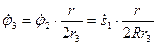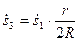
Подставив их в выражение для кинетической энергии, получим:
.
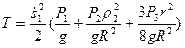При записи результата учтено, что осевой момент инерции для соосных дисков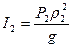 
, а для однородного диска 
.
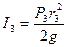Продифференцировав выражение для кинетической энергии по времени, получим левую часть равенства (19):
.
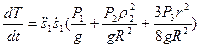Отметим, что в рассматриваемой системе внутренние связи не деформируемы, поэтому мощность внутренних сил должна быть равна нулю. Запишем выражение для мощности внешних сил:
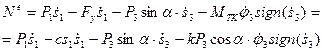
при записи учтено, что сила упругости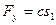 
, мощность силы сцепления и силы нормального давления, приложенных в мгновенном центре скоростей, равна нулю, а 
.
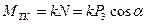В выражение мощности подставим скорость центра и угловую скорость диска, выраженные через скорость первого груза. Тогда
.
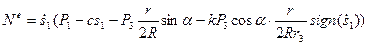Приравняем выражения для левой и правой частей равенства (19); сократим их на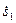 
. Перенесем переменные величины в левую часть равенства и поделим все слагаемые на постоянный коэффициент при ускорении первого груза. Окончательный вид искомого дифференциального уравнения будет
,
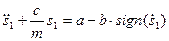где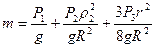 
; 
; 
.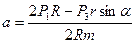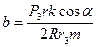