Краткие сведения из курса механики, позволяющие получить математическую модель задачи

ОГЛАВЛЕНИЕ

1. Исходные данные и постановка задачи

1.1. Исходные данные

1.2. Постановка задачи

1.3. Требования к оформлению и содержанию работы

2. Краткие сведения из курса механики, позволяющие получить математическую модель задачи

2.1. Кинематика простейших передач. Кинематика плоско - параллельного движения тела.

2.2. Дифференциальные уравнения поступательного, вращательного и плоско – параллельного движения тела

2.3. Нахождение параметров равновесия (покоя) механической системы

2.4. Теорема об изменении кинетической энергии механической системы

2.5. Нахождение параметров движения при наличии трения скольжения и трения качения

2.6. Выбор контрольного параметра и получение формул для вычисления исследуемых параметров

3. Численное моделирование процесса движения механической системы методом Эйлера

3.1. Краткие сведения о методе Эйлера

3.2. Получение рекуррентных зависимостей для моделирования процесса движения

3.3. Описание алгоритма расчета

3.4. Составление программы расчета

3.5. Результаты расчета и их анализ

4. Список литературы

Исходные данные и постановка задачи

Исходные данные

Исходными данными для каждого из вариантов курсовой работы служат:

1) кинематическая схема механической системы с одной степенью свободы; система состоит из нескольких твердых тел, связанных между собой нерастяжимыми нитями; одно из тел связано с неподвижным основанием пружиной;

2) необходимые геометрические размеры;

3) инерционные характеристики всех твердых тел; жесткость пружины;

4) величины и направления активных усилий, приложенных к твердым телам; коэффициенты трения скольжения и трения качения;

5) начальные условия, определяющие положения и скорости тел в начальный момент времени.

Варианты кинематических схем и числовые данные находятся на стенде «Задание по динамике» кафедры теоретической механики.

Постановка задачи

Для указанного преподавателем варианта курсовой работы студент должен разработать:

- математическую модель для расчета параметров равновесия тел механической системы;

- математическую модель в виде системы дифференциальных и алгебраических уравнений для расчета параметров движения тел механической системы и реакций во внешних и внутренних связях;

- математическую модель для расчета параметров движения одного из тел механической системы в форме дифференциального уравнения второго порядка; для получения уравнения следует воспользоваться теоремой об изменении кинетической энергии;

- комплект формул для расчета контрольного параметра, а так же указанных преподавателем параметров механической системы, для которых необходимо проведение исследования;

- структурированный алгоритм расчета параметров движения одного из тел механической системы, а так же контрольного и исследуемых параметров; решение дифференциального уравнения следует выполнить указанным преподавателем методом численного интегрирования Эйлера;

- закодировать алгоритм средствами языка программирования высокого уровня, указанного преподавателем;

- активизировать программу и выполнить расчеты с заданной точностью;

- сравнить полученные результаты с известным решением;

- выполнить численное исследование влияния начальных условий на исследуемые параметры.

Примечание: для студентов некоторых специальностей проведение численного исследования может быть исключено.

1.3. Требования к оформлению и содержанию работы

В качестве результата необходимо предъявить:

- диск, содержащий файлы разработанной программы;

- пояснительную записку.

Структура пояснительной записки:

1. Титульный лист.

На титульном листе необходимо:

- сверху указать полное название университета,

- посередине указать название курсовой работы «Расчет параметров движения (равновесия) механической системы» и номер ее варианта,

- ниже и правее – указать, кем работа выполнена (номер учебной группы студента, его фамилия и инициалы) и кем должна быть проверена (должность, фамилия и инициалы преподавателя),

- внизу указывается место (Санкт-Петербург) и год выполнения работы.

2. Содержание.

Содержание включает разделы и подразделы курсовой работы с указанием номеров страниц.

3. Задание на курсовую работу.

На странице должна быть изображена кинематическая схема механической системы в масштабе с указанием всех заданных размеров и активных сил. Ниже кратко формулируется условие поставленной задачи с указанием всех заданных величин, а так же и искомых и исследуемых величин и зависимостей.

4. Разработка математических моделей.

Этот раздел следует разделить на несколько подразделов.

В пером из них рекомендуется составить уравнения кинематических связей. При этом для тел механической системы вводятся координаты, определяющие их положение (обычно это линейные и (или) угловые координаты). Вид соотношений между ними зависит от кинематической схемы механической системы, а составляются эти соотношения с учетом следующих физических допущений: нити являются нерастяжимыми и не скользят относительно блоков, блоки не скользят относительно друг друга и поверхностей, по которым осуществляется качение (см. [3], [6]).

Во втором подразделе для расчета параметров движения тел механической системы и реакций во внешних и внутренних связях должна быть получена математическая модель в виде системы дифференциальных и алгебраических уравнений. При этом механической системе задается движение в какую-то сторону (на усмотрение студента); система мысленно разделяется на отдельные тела, для каждого из которых рисуется силовая схема с указанием выбранных координат. Полученные силовые схемы позволяют для каждого из тел написать дифференциальные уравнения движения (по некоторым координатам – уравнения равновесия). Эти уравнения, а так же уравнения кинематических связей, выражения для силы упругости, силы трения скольжения и момента трения качения, должны составить замкнутую систему из дифференциальных и алгебраических уравнений относительно неизвестных параметров движения и реакций внешних и внутренних связей. Решение полученной замкнутой системы уравнений возможно, но в настоящей работе не требуется.

Замечание: наличие в системе силы трения скольжения и (или) момента трения качения приводит, при смене направления скорости движения механической системы, к смене знака у этих слагаемых. Таким образом, дифференциальные уравнения, описывающие движения механической системы с положительной и отрицательной скоростью, будут отличаться своей правой частью (см. учет трения скольжения в [1], [3], [7]).

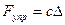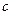В третьем подразделе должна быть получена математическую модель для расчета параметров равновесия тел механической системы. Для расчета параметров равновесия следует в дифференциальных уравнениях движения положить ускорения (линейные и угловые) равными нулю, а силу упругости пружины ; где - коэффициент жесткости пружины при растяжении, а 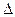- удлинение пружины в положении статического равновесия механической системы. Полученная система алгебраических уравнений позволяет найти удлинение пружины в положении статического равновесия механической системы.

Замечание: наличие в системе силы трения скольжения и (или) момента трения качения приводит, при смене положительного направления осей для тел механической системы, к смене знака у всех слагаемых, кроме вышеуказанных. Таким образом, алгебраические уравнения, описывающие равновесие механической системы в разные стороны, будут отличаться; отмеченная особенность позволит вычислить два значения (наибольшее и наименьшее) величины удлинения пружины. Вывод: рассматриваемая механическая система будет находиться в равновесии при любом удлинении пружины, лежащем в диапазоне .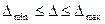

В четвертом подразделе должна быть получена математическая модель для расчета параметров движения одного из тел механической системы в форме дифференциального уравнения второго порядка; для получения уравнения следует воспользоваться теоремой об изменении кинетической энергии.

Замечание: как уже говорилось, должны быть получены два неоднородных дифференциальных уравнения, отличающихся правыми частями.

В пятом подразделе необходимо получить комплект формул для расчета контрольного параметра, а так же указанных преподавателем параметров механической системы, для которых необходимо проведение численного исследования.

5. Разработка структурированного алгоритма.

В этом разделе должен быть разработан структурированный алгоритм расчета параметров движения одного из тел механической системы, контрольного параметра, а так же параметров механической системы, для которых необходимо проведение исследования; решение дифференциального уравнения следует выполнить указанным преподавателем методом численного интегрирования Эйлера.

6. Разработка программы расчета.

В этом разделе необходимо закодировать алгоритм средствами языка программирования высокого уровня, указанного преподавателем. Привести листинг программы.

7. Выполнение расчетов и анализ полученных результатов.

В этом разделе необходимо привести результаты выполненных расчетов и их сравнение с величинами параметров движения, найденных по аналитическим зависимостям из [1], [5].

8. Список использованных источников.

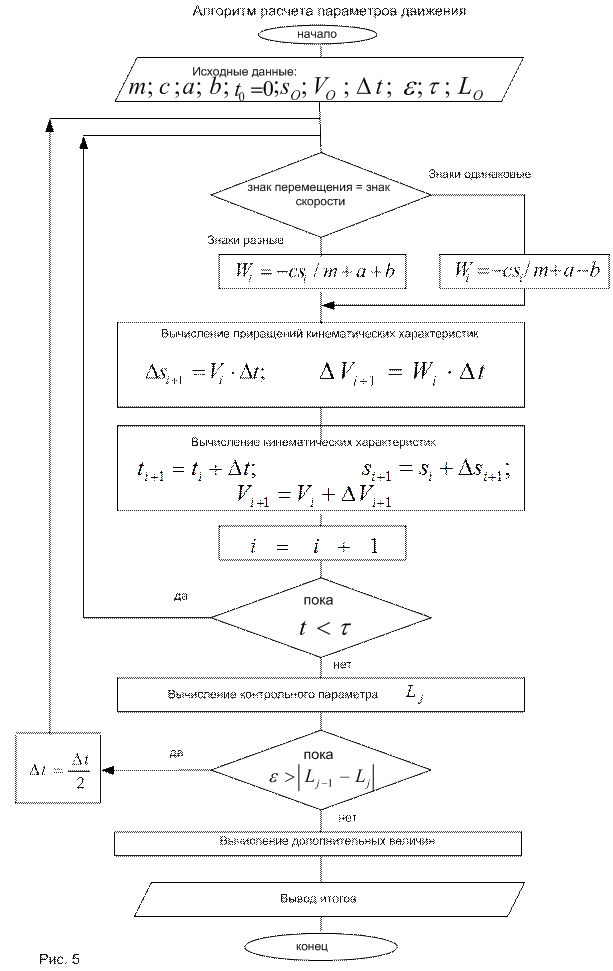
Описание алгоритма расчета

Исходные данные задачи:

- предварительно вычисленные величины: ;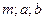

- заданные величины: .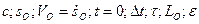

Здесь 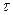- время длительности процесса, 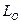- начальное значение контрольного параметр расчета (например – наибольшее отклонение груза от начала отсчета), а 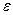- величина погрешности при расчете контрольного параметра.

Сформулируем алгоритм расчета параметров движения (положение, скорость и ускорение) для груза механической системы.

1. Производится сравнение знаков перемещения и скорости для момента времени 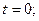выбирается вариант вычисления величины .

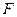2. По заданным начальным условиям вычисляется значение ускорения в начальный момент времени как .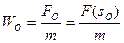

3. Вычисляются значения приращений перемещения и скорости груза как

.

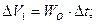
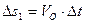4. Вычисляются значения перемещения и скорости груза в момент времени 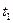как

.

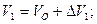
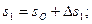
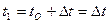5. Вычисленные величины сохраняются в созданной базе данных .

6. Сравнивается вычисленное значение времени 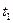с заданным временем расчета процесса .

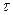Если 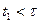расчет продолжается возвратом к первому пункту алгоритма.

При 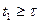происходит переход к анализу погрешности вычислений.

7. Вычисляется (или присваивается) значение контрольного параметра 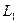. Заданное значение погрешности 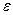позволяет выполнить сравнение величин 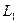и 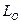. Если отличие не превышает величины 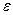, расчет кинематических характеристик заканчивается и происходит переход к расчету дополнительных величин. В противном случае расчет повторяется с уменьшенным вдвое шагом интегрирования по времени ( ).

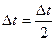8. Вычисляются дополнительные величины, указанные преподавателем (например, реакции внутренних и внешних связей и т.п.). Значения величин сохраняются в созданной базе данных.

Замечание: выполнение такого расчета теперь не вызывает затруднений – для этого в дифференциальные уравнения движения тел механической системы следует подставить найденные значения перемещения, скорости и ускорения для любого момента времени и решить систему алгебраических уравнений относительно неизвестных величин.

9. Сохраненные в базах данных величины (см. п.п. 5 и 8) выводятся на печать.

ОГЛАВЛЕНИЕ

1. Исходные данные и постановка задачи

1.1. Исходные данные

1.2. Постановка задачи

1.3. Требования к оформлению и содержанию работы

2. Краткие сведения из курса механики, позволяющие получить математическую модель задачи

2.1. Кинематика простейших передач. Кинематика плоско - параллельного движения тела.

2.2. Дифференциальные уравнения поступательного, вращательного и плоско – параллельного движения тела

2.3. Нахождение параметров равновесия (покоя) механической системы

2.4. Теорема об изменении кинетической энергии механической системы

2.5. Нахождение параметров движения при наличии трения скольжения и трения качения

2.6. Выбор контрольного параметра и получение формул для вычисления исследуемых параметров

3. Численное моделирование процесса движения механической системы методом Эйлера

3.1. Краткие сведения о методе Эйлера

3.2. Получение рекуррентных зависимостей для моделирования процесса движения

3.3. Описание алгоритма расчета

3.4. Составление программы расчета

3.5. Результаты расчета и их анализ

4. Список литературы

Исходные данные и постановка задачи

Исходные данные

Исходными данными для каждого из вариантов курсовой работы служат:

1) кинематическая схема механической системы с одной степенью свободы; система состоит из нескольких твердых тел, связанных между собой нерастяжимыми нитями; одно из тел связано с неподвижным основанием пружиной;

2) необходимые геометрические размеры;

3) инерционные характеристики всех твердых тел; жесткость пружины;

4) величины и направления активных усилий, приложенных к твердым телам; коэффициенты трения скольжения и трения качения;

5) начальные условия, определяющие положения и скорости тел в начальный момент времени.

Варианты кинематических схем и числовые данные находятся на стенде «Задание по динамике» кафедры теоретической механики.

Постановка задачи

Для указанного преподавателем варианта курсовой работы студент должен разработать:

- математическую модель для расчета параметров равновесия тел механической системы;

- математическую модель в виде системы дифференциальных и алгебраических уравнений для расчета параметров движения тел механической системы и реакций во внешних и внутренних связях;

- математическую модель для расчета параметров движения одного из тел механической системы в форме дифференциального уравнения второго порядка; для получения уравнения следует воспользоваться теоремой об изменении кинетической энергии;

- комплект формул для расчета контрольного параметра, а так же указанных преподавателем параметров механической системы, для которых необходимо проведение исследования;

- структурированный алгоритм расчета параметров движения одного из тел механической системы, а так же контрольного и исследуемых параметров; решение дифференциального уравнения следует выполнить указанным преподавателем методом численного интегрирования Эйлера;

- закодировать алгоритм средствами языка программирования высокого уровня, указанного преподавателем;

- активизировать программу и выполнить расчеты с заданной точностью;

- сравнить полученные результаты с известным решением;

- выполнить численное исследование влияния начальных условий на исследуемые параметры.

Примечание: для студентов некоторых специальностей проведение численного исследования может быть исключено.

1.3. Требования к оформлению и содержанию работы

В качестве результата необходимо предъявить:

- диск, содержащий файлы разработанной программы;

- пояснительную записку.

Структура пояснительной записки:

1. Титульный лист.

На титульном листе необходимо:

- сверху указать полное название университета,

- посередине указать название курсовой работы «Расчет параметров движения (равновесия) механической системы» и номер ее варианта,

- ниже и правее – указать, кем работа выполнена (номер учебной группы студента, его фамилия и инициалы) и кем должна быть проверена (должность, фамилия и инициалы преподавателя),

- внизу указывается место (Санкт-Петербург) и год выполнения работы.

2. Содержание.

Содержание включает разделы и подразделы курсовой работы с указанием номеров страниц.

3. Задание на курсовую работу.

На странице должна быть изображена кинематическая схема механической системы в масштабе с указанием всех заданных размеров и активных сил. Ниже кратко формулируется условие поставленной задачи с указанием всех заданных величин, а так же и искомых и исследуемых величин и зависимостей.

4. Разработка математических моделей.

Этот раздел следует разделить на несколько подразделов.

В пером из них рекомендуется составить уравнения кинематических связей. При этом для тел механической системы вводятся координаты, определяющие их положение (обычно это линейные и (или) угловые координаты). Вид соотношений между ними зависит от кинематической схемы механической системы, а составляются эти соотношения с учетом следующих физических допущений: нити являются нерастяжимыми и не скользят относительно блоков, блоки не скользят относительно друг друга и поверхностей, по которым осуществляется качение (см. [3], [6]).

Во втором подразделе для расчета параметров движения тел механической системы и реакций во внешних и внутренних связях должна быть получена математическая модель в виде системы дифференциальных и алгебраических уравнений. При этом механической системе задается движение в какую-то сторону (на усмотрение студента); система мысленно разделяется на отдельные тела, для каждого из которых рисуется силовая схема с указанием выбранных координат. Полученные силовые схемы позволяют для каждого из тел написать дифференциальные уравнения движения (по некоторым координатам – уравнения равновесия). Эти уравнения, а так же уравнения кинематических связей, выражения для силы упругости, силы трения скольжения и момента трения качения, должны составить замкнутую систему из дифференциальных и алгебраических уравнений относительно неизвестных параметров движения и реакций внешних и внутренних связей. Решение полученной замкнутой системы уравнений возможно, но в настоящей работе не требуется.

Замечание: наличие в системе силы трения скольжения и (или) момента трения качения приводит, при смене направления скорости движения механической системы, к смене знака у этих слагаемых. Таким образом, дифференциальные уравнения, описывающие движения механической системы с положительной и отрицательной скоростью, будут отличаться своей правой частью (см. учет трения скольжения в [1], [3], [7]).

В третьем подразделе должна быть получена математическую модель для расчета параметров равновесия тел механической системы. Для расчета параметров равновесия следует в дифференциальных уравнениях движения положить ускорения (линейные и угловые) равными нулю, а силу упругости пружины 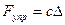; где 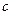- коэффициент жесткости пружины при растяжении, а 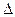- удлинение пружины в положении статического равновесия механической системы. Полученная система алгебраических уравнений позволяет найти удлинение пружины в положении статического равновесия механической системы.

Замечание: наличие в системе силы трения скольжения и (или) момента трения качения приводит, при смене положительного направления осей для тел механической системы, к смене знака у всех слагаемых, кроме вышеуказанных. Таким образом, алгебраические уравнения, описывающие равновесие механической системы в разные стороны, будут отличаться; отмеченная особенность позволит вычислить два значения (наибольшее и наименьшее) величины удлинения пружины. Вывод: рассматриваемая механическая система будет находиться в равновесии при любом удлинении пружины, лежащем в диапазоне .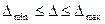

В четвертом подразделе должна быть получена математическая модель для расчета параметров движения одного из тел механической системы в форме дифференциального уравнения второго порядка; для получения уравнения следует воспользоваться теоремой об изменении кинетической энергии.

Замечание: как уже говорилось, должны быть получены два неоднородных дифференциальных уравнения, отличающихся правыми частями.

В пятом подразделе необходимо получить комплект формул для расчета контрольного параметра, а так же указанных преподавателем параметров механической системы, для которых необходимо проведение численного исследования.

5. Разработка структурированного алгоритма.

В этом разделе должен быть разработан структурированный алгоритм расчета параметров движения одного из тел механической системы, контрольного параметра, а так же параметров механической системы, для которых необходимо проведение исследования; решение дифференциального уравнения следует выполнить указанным преподавателем методом численного интегрирования Эйлера.

6. Разработка программы расчета.

В этом разделе необходимо закодировать алгоритм средствами языка программирования высокого уровня, указанного преподавателем. Привести листинг программы.

7. Выполнение расчетов и анализ полученных результатов.

В этом разделе необходимо привести результаты выполненных расчетов и их сравнение с величинами параметров движения, найденных по аналитическим зависимостям из [1], [5].

8. Список использованных источников.

Краткие сведения из курса механики, позволяющие получить математическую модель задачи