Шкала оценивания знаний, навыков умений (владений) опыта деятельности
Учебным планом по учебной дисциплине «Методика преподавания математики в начальной школе» предусмотрен экзамен. Оценка знаний, навыков, умений (владений) опыта деятельности осуществляется по четырехбалльной шкале оценивания «отлично», «хорошо», «удовлетворительно», «неудовлетворительно».
7.4.2 Шкала оценивания уровня (этапа) сформированности компетенции
Компетенция сформирована на базовом уровне:
на «отлично», если не менее 65% показателей оценены не ниже отлично на базовом и повышенном уровне, а остальные не ниже «хорошо».
на «хорошо», если не менее 65% показателей оценены не ниже «хорошо» на базовом и повышенном уровне, а остальные не ниже «удовлетворительно».
на «удовлетворительно», если не менее 65% показателей оценены не ниже «удовлетворительно» на базовом и повышенном уровне.
Компетенция сформирована на повышенном уровне:
на «отлично», если не менее 65% показателей оценены не ниже отлично на повышенном уровне, а остальные не ниже «хорошо» на повышенном и базовом уровне.
на «хорошо», если не менее 65% показателей оценены не ниже «хорошо» на повышенном уровне, а остальные не ниже «удовлетворительно» на базовом и повышенном уровне.
на «удовлетворительно», если не менее 65% показателей оценены не ниже «удовлетворительно» на повышенном уровне.
7.5. Типовые контрольные задания или иные материалы, необходимые для оценки знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций в процессе освоения образовательной программы
7.5 Типовые контрольные задания или иные материалы, необходимые для оценки знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования компетенций в процессе освоения образовательной программы
7.5.1. Схема соответствия типовых контрольных заданий и оцениваемых знаний, умений, навыков и (или) опыта деятельности, характеризующих этапы формирования
| № | Формируемая компетенция | Показатели сформированности компетенции | Номер типового контрольного задания |
| 1.. | готовность реализовывать образовательные программы по учебному предмету в соответствии с требованиями образовательных стандартов(ПК-1) | ПК-П–В1ПК-Б–В1 | Анализ и оценка результатов выполнения заданий ПК-Б–В16.3.1, 6.3.2, ПК-П–В1 6.3.1, 6.3.2 |
| ПК-П–В2ПК-Б–В2 | Анализ и оценка результатов выполнения заданий ПК-П–В2 6.3.3,6.3.4, ПК-Б–В2 6.3.3,6.3.4 | ||
| ПК--П–В3ПК--Б–В3 | Анализ и оценка результатов выполнения заданий ПК--Б–В3 6.3.5, 6.3.6, ПК--П–В36.3.5, 6.3.6, | ||
| ПК-П–В4ПК--Б–В4 | Анализ и оценка результатов выполнения заданий ПК--Б–В4 6.3.7, 6.3.8, ПК-П–В4 6.3.7, 6.3.8, | ||
| ПК-П–В5ПК--Б–В5 | Анализ и оценка результатов выполнения заданий ПК--Б–В5 6.3.9, 6.3.10, ПК-П–В56.3.9, 6.3.10, | ||
| ПК-П–В6ПК--Б–В6 | Анализ и оценка результатов выполнения заданий ПК--Б–В66.3.11, 6.3.12, ПК-П–В66.3.11, 6.3.12, | ||
| ПК-П–В7ПК--Б–В7 | Анализ и оценка результатов выполнения заданий ПК-П–В7 6.3.13,6.3.14, ПК-Б–В7 6.3.13,6.3.14 | ||
| ПК-П–В8ПК--Б–В8 | Анализ и оценка результатов выполнения заданий ПК-П–В8 6.3.15,6.3.16, ПК-Б–В8 6.3.15,6.3.16 | ||
| ПК-П–В9ПК--Б–В9 | Анализ и оценка результатов выполнения заданий ПК-П–В9 6.3.17,6.3.18, ПК-Б–В9 6.3.17,6.3.18 | ||
| ПК-П–В10ПК--Б–В10 | Анализ и оценка результатов выполнения заданий ПК-П–В10 6.3.19,6.3.20, ПК-Б–В10 6.3.19,6.3.20 | ||
| ПК-1-П–У1ПК-1-Б–У1 | Анализ и оценка результатов выполнения заданий ПК-1-П–У16.2.1,6.2.2, ПК-1-Б–У16.2.1,6.2.2, | ||
| ПК-1-П–У2 ПК-1-Б–У2 | Анализ и оценка результатов выполнения заданий ПК-1-П–У2 6.2.3,6.2.4, ПК-1-Б–У26.2.3,6.2.4, | ||
| ПК-1-П–У3 ПК-1-Б–У3 | Анализ и оценка результатов выполнения заданий ПК-1-П–У3 6.2.5,6.2.6, ПК-1-Б–У36.2.5,6.2.6, | ||
| ПК-1-П–У4 ПК-1-Б–У4 | Анализ и оценка результатов выполнения заданий ПК-1-П–У4 6.2.7,6.2.8 ПК-1-Б–У4 6.2.7,6.2.8 | ||
| ПК-1-П–У5 ПК-1-Б–У5 | Анализ и оценка результатов выполнения заданий ПК-1-П–У5 6.2.9,6.2.10, ПК-1-Б–У56.2.9,6.2.10, | ||
| ПК-1-П–У6 ПК-1-Б–У6 | Анализ и оценка результатов выполнения заданий ПК-1-П–У6 6.2.11,6.212, ПК-1-П–У6 6.2.11,6.212, | ||
| ПК-1-П–У7 ПК-1-Б–У7 | Анализ и оценка результатов выполнения заданий ПК-1-П–У7 6.2.13,6.214, ПК-1-П–У7 6.2.13,6.2.14, | ||
| ПК-1-П–У8 ПК-1-Б–У8 | Анализ и оценка результатов выполнения заданий ПК-1-П–У8 6.2.15,6.216, ПК-1-П–У8 6.2.15,6.2.16, | ||
| ПК-1-П–У9 ПК-1-Б–У9 | Анализ и оценка результатов выполнения заданий ПК-1-П–У9 6.2.17,6.218, ПК-1-П–У9 6.2.17,6.218, | ||
| ПК-1-П–У10ПК-1-Б–У10 | Анализ и оценка результатов выполнения заданий ПК-1-П–У10 6.2.19,6.220, ПК-1-П–У10 6.2.19,6.2.20, | ||
| ПК-1-П–З1 ПК-1-Б–З1 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З1 6.1.1,6.1.2., ПК-1-Б–З1 6.1.1,6.1.2., | ||
| ПК-1-П–З2 ПК-1-Б–З2 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З2 6.1.3,6.1.4., , ПК-1-Б–З2 6.1.3,6.1.4., | ||
| ПК-1-П–З3 ПК-1-Б–З3 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З3 6.1.5,6.1.6., ПК-1-Б–З3 6.1.5,6.1.6., | ||
| ПК-1-П–З4 ПК-1-Б–З4 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З4 6.1.7,6.1.8., ПК-1-Б–З4 6.1.7,6.1.8 | ||
| ПК-1-П–З5 ПК-1-Б–З5 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З5 6.1.9,6.1.10 ПК-1-Б–З5 6.1.9,6.1.10 | ||
| ПК-1-П–З6 ПК-1-Б–З6 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З6 6.1.11,6.1.12., ПК-1-Б–З66.1.11,6.1.12 | ||
| ПК-1-П–З7 ПК-1-Б–З7 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З7 6.1.13,6.1.14., ПК-1-Б–З7 6.1.13,6.1.14 | ||
| ПК-1-П–З8 ПК-1-Б–З8 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З8 6.1.15,6.1.16 ПК-1-Б–З8 6.1.15,6.1.16 | ||
| ПК-1-П–З9 ПК-1-Б–З9 | Вопросы к экзамену . Анализ и оценка результатов выполнения заданий ПК-1-П–З9 6.1.18,6.1.17., ПК-1-Б–З9. 6.1.17,6.1.18 | ||
| ПК-1-П–З10 ПК-1-Б–З10 | Анализ и оценка результатов выполнения заданий ПК-1-П–З10 6.1.19,6.1. 20., ПК-1-Б–З10 6.1.19,6.1.20 Вопросы к экзамену . |
Задания для оценки знаний
Примерный перечень вопросов к экзамену
БАЗОВЫЙ УРОВЕНЬ
1. Методика изучения нумерации чисел в пределах десятка.
2. Методика изучения нумерации чисел в пределах сотни.
3. Методика изучения нумерации чисел в пределах тысячи.
4. Методика изучения нумерации чисел в пределах миллиона.
5. Первоначальное ознакомление учащихся с действиями сложения и вычитания.
6. Методика обучения решению простых задач на вычитание.
7. Методика изучения устных приёмов сложения и вычитания многозначных чисел.
8. Методика изучения письменных приёмов сложения и вычитания многозначных чисел.
9. Ознакомление учащихся действиям деления.
10. Методика обучения решению простых задач на умножение.
11. Методика обучения решению простых задач на деление.
12. Методика изучения устных приёмов умножения.
13. Методика изучения устных приёмов деления.
14. Методика формирования письменных приёмов умножения.
15. Методика изучения деления с остатком.
16. Методика формирования письменных приёмов деления.
17. Методика обучения решению составных задач.
18. Ознакомление учащихся со свойствами сложения, их применение при вычислениях.
19. Методика ознакомления с приёмами вычитания, их применение при вычислениях.
20. Методика ознакомления со свойствами умножения, их применение при вычислениях.
21. Методика изучения переместительного свойства умножения. Таблица умножения и соответствующие случаи деления.
22. Методика изучения внетабличных случаев умножения и деления.
23. Методика ознакомления со свойствами деления, их применение при вычислениях.
24. Изучение алгоритма письменного деления многозначного числа на двузначное и трехзначное число.
25. Методика формирования представлений о выражении.
26. Равенства и неравенства в начальном курсе математики.
27. Формирование представлений об уравнении. Методика обучения решению простейших уравнений.
28. Методика ознакомления учащихся с простейшими геометрическими фигурами (точкой, отрезком, ломаной, многоугольником, кругом, углом, прямоугольником).
29. Понятие периметра многоугольников. Формула периметра прямоугольника. Решение задач.
30. Методика ознакомления учащихся с длиной отрезка, с единицами её измерения.
31. Методика ознакомления учащихся с массой, с единицами её измерения.
32. Методика ознакомления учащихся со скоростью, с единицами её измерения.
33. Методика ознакомления учащихся со временем, с единицами его измерения.
34. Методика формирования представлений о площади фигуры.
35. Понятие «текстовая арифметическая задача» в начальном курсе математики.
36. Роль и функции текстовых задач.
37. Подготовительная работа к решению задач.
38. Ознакомление с решением задач.
39. Методика работы над простыми задачами, раскрывающими конкретный смысл арифметических действий сложения и вычитания.
40. Методика работы над простыми задачами, раскрывающими конкретный смысл арифметических действий умножения и деления.
41. Методика работы над простыми задачами, раскрывающими связь между компонентами и результатами арифметических действий
42. Методика работы над простыми задачами, раскрывающими понятия разностного отношения
43. Методика работы над простыми задачами, раскрывающими понятия кратного отношения
44. Способы решения задачи.
45. Обучение проверке решения задачи.
46. Первоначальное знакомство с составной задачей.
47. Методика работы над задачами, связанными с пропорциональными величинами.
48. Ознакомление учащихся со скоростью движения тел. Средняя скорость движения. Взаимосвязь между величинами: скорость, время, расстояние.
49. Методика обучения решению текстовых задач, связанных с движением тел.
50. Решение задач алгебраическим способом.
51. Решение нестандартных задач, как эффективное средство развития познавательных способностей учащихся.
52. Методика обучения решению логических задач
53. Методика обучения решению комбинаторных задач
54. Наглядные средства обучения решению текстовых арифметических задач.
55. Элементарные геометрические построения с использованием линейки, циркуля и чертежного угольника.
56. Особенности устных и письменных вычислений. Общие и частные приемы устных вычислений.
57. Формирование у младших школьников представления о дроби, сравнение дробей.
58. Формирование представлений и понятий о геометрических фигурах, изучаемых в начальной школе
59. Изучение устных приемов деления чисел первой тысячи, многозначных чисел.
60. Изучение письменных приемов умножения чисел первой тысячи, многозначных чисел.
ПОВЫШЕННЫЙ УРОВЕНЬ
1. Анализ различных концепций построения начального курса математики.
2. Сравнительный анализ альтернативных программ по математике в начальных классах (Модель «Начальная школа 21 века» «Школа 2000…» - «Школа 2100» «Гармония», система Л.В. Занкова и система Д.Б. Эльконина – В.В. Давыдова.).
3. Метапредметные и предметные планируемые результаты обучения математики согласно требованиям ФГОС
4. Проблемное обучение на уроках математики
5. Приемы активизации познавательной деятельности на уроках математики
6. Индивидуальный подход к обучению на уроках математики
7. Внеклассная работа по математике.
8. Реализация основных положений теории учебной деятельности в процессе обучения младших школьников математике.
9. Приёмы умственных действий и их формирование у младших школьников при обучении математике
10. Развитие логического и алгоритмического мышления младших школьников.
Тестовые задания
(правильный вариант ответов – вариант «a»)
1. Главное содержание начального курса математики составляет:
а) арифметический материал;
б) алгебраический материал;
в) геометрический материал;
2. В курсе математики начальной школы выделено концентров:
а) 4;
б) 5;
в) 3;
3. В процессе выполнения операций объединения множеств, не имеющих общих элементов, раскрывается:
а) сложение;
б) вычитание;
в) умножение;
4. В процессе выполнения операций удаления части множества (подмножества), раскрывается:
а) вычитание;
б) сложение;
в) умножение;
5. В процессе выполнения операций объединения множеств одинаковой численности, раскрывается:
а) умножение;
б) сложение;
в) вычитание;
6. В процессе выполнения операций разбиения множества на ряд равночисленных множеств, раскрывается:
а) деление;
б) умножение;
в) вычитание;
7. Одним из центральных понятий начального курса математики является понятие:
а) натурального числа;
б) целого числа;
в) положительного числа;
8. Для обозначения отсутствия единиц какого-либо разряда или класса в записи числа используют:
а) цифру нуль;
б) _ ;
в) пропуск клеточки в тетради;
9. Переместительному свойству сложения соответствует формула:
а) a+b = b+a;
б) a · b = b · a;
в) a · (b+c) = a · b+a · c;
10. Переместительному свойству умножения соответствует формула:
а) a · b = b · a;
б) a+b = b+a;
в) a · (b+c) = a · b+a · c;
11. Свойству прибавления числа к сумме соответствует формула:
а) (a+b)+c = a+(b+c);
б) a+b = b+a;
в) a · b = b · a;
12. Свойству умножения произведения на число соответствует формула:
а) (a · b) · c = a · (b · c);
б) (a+b)+c = a+(b+c);
в) a · (b+c) = a · b+a · c;
13. Распределительному свойству умножения соответствует формула:
а) a · (b+c) = a · b+a · c;
б) a+b = b+a;
в) (a · b) · c = a · (b · c);
14. Свойству деления суммы на число соответствует формула:
а) (а + b) : с = а : с + b : с;
б) а : (b : с) = (а : b) · с;
в) a : (b · c) = a : b : c;
15. Свойству деления числа на произведение соответствует формула:
а) a : (b · c) = a : b : c;
б) а · (b : с) = (а · b) : с
в) (а + b) : с = а : с + b : с;
16. Свойству умножения числа на частное соответствует формула:
а) а · (b : с) = (а · b) : с;
б) a : (b · c) = a : b : c;
в) (а + b) : с = а : с + b : с;
17. Свойству деления числа на частное соответствует формула:
а) а : (b : с) = (а : b) · с;
б) а · (b : с) = (а · b) : с;
в) a : (b · c) = a : b : c;
18. Если в качестве приоритетной цели урока выступает формирование знаний, умений и навыков, то учебные задания выстраиваются на уроке обычно в такой последовательности:
а) задания на подражание, тренировочные задания, частично–поисковые или творческие задания;
б) тренировочные задания, задания на подражание, частично–поисковые или творческие задания;
в) тренировочные задания, частично–поисковые или творческие задания, задания на подражание;
19. Наиболее распространённым типом урока математики в начальных классах являются:
а) комбинированные уроки;
б) уроки – лекции;
в) уроки формирования новых знаний;
20. Изучением психического развития ребёнка занимается:
а) психология;
б) методика математики;
в) педагогика;
21. Операция мысленного или реального расчленения целого на составные части, выполняемая в процессе познания или предметно–практической деятельности человека – это:
а) анализ;
б) синтез;
в) суждение;
22. Сходство в каком-либо отношении между предметами, явлениями, понятиями, способами действий – это:
а) аналогия;
б) анализ;
в) синтез;
23. Процесс соединения или объединения ранее разрозненных вещейилипонятийв целое или набор – это:
а) синтез;
б) анализ;
в) логическое мышление;
24. Форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами – это:
а) суждение;
б) умозаключение;
в) логическое мышление;
25. Мыслительный процесс, в ходе которого из одного или нескольких суждений, называемых посылками, выводится новое суждение, называемое заключением, или следствием – это:
а) умозаключение;
б) логическое мышление;
в) сравнение;
26. Элементы информации, связанные между собой и с внешним миром – это:
а) знания;
б) умения;
в) навыки;
27. Владение способами применения усваиваемых знаний на практике – это:
а) умение;
б) знания;
в) навыки;
28. Составной элемент умения, как автоматизированное действие, доведённое до высокой степени совершенства – это:
а) навык;
б) знания;
в) умения;
29. Целенаправленный процесс взаимодействия учителя и учащихся, в ходе которого происходит усвоение знаний, умений и навыков, осуществляется воспитание и развитие учащихся – это:
а) обучение;
б) дрессировка;
в) урок;
30. Вид мыслительного процесса, при котором человек использует логические конструкции и готовые понятия – это:
а) логическое мышление;
б) анализ;
в) синтез;
31. Суждения, в которых что-то утверждается или отрицается относительно одного предмета, называют:
а) единичными;
б) частными;
в) общими;
32. Суждения, в которых что-то утверждается или отрицается относительно некоторой совокупности предметов из данного класса или относительно некоторого подмножества данного множества предметов, называют:
а) частными;
б) единичными;
в) общими;
33. Суждения, в которых что-то утверждается или отрицается относительно всех предметов данной совокупности, называют:
а) общими;
б) частными;
в) единичными;
34. Выберете верный порядок этапов работы над арифметической задачей:
а) Работа над содержанием задачи. Поиск решения задачи. Решение задачи. Формулировка ответа.
б) Поиск решения задачи. Работа над содержанием задачи. Решение задачи. Формулировка ответа.
в) Поиск решения задачи. Решение задачи. Работа над содержанием задачи. Формулировка ответа.
35. Задача «У Маши было 6 шариков. 3 шарика он подарила сестре. Сколько шариков у Маши осталось?» – это задача на:
а) нахождение остатка;
б) нахождение суммы;
в) разностное сравнение;
36. Задача «Дима сорвал 6 слив, а Нина сорвала 4 сливы. Сколько всего слив сорвали Нина и Дима?» – задача на:
а) нахождение суммы;
б) увеличение числа на несколько единиц;
в) разностное сравнение;
37. Задача «У Коли 9 марок. А у Пети 7 марок. На сколько у Коли марок больше, чем у Пети?» – задача на:
а) разностное сравнение;
б) уменьшение числа на несколько единиц;
в) нахождение остатка;
38. Задача «У девочки было несколько шаров. Когда она отдала подруге 3 шара. У неё осталось 5 шаров. Сколько шаров было у девочки?» – задача на:
а) взаимосвязь между компонентами и результатом вычитания;
б) разностное сравнение;
в) нахождение остатка;
39. Задача «Две девочки разделили 6 шаров поровну. Сколько шаров получила каждая?» – задача на:
а) нахождение частного;
б) разностное сравнение;
в) деление;
40. Задача «К кормушке прилетели 8 снегирей и 2 синицы. Во сколько раз снегирей больше, чем синиц?» – задача на:
а) сравнение чисел с помощью операции деления (на кратное сравнение);
б) нахождение частного;
в) деление;
41. Задача «С одной грядки собрали 4 мешка картофеля, а с другой – 6 таких же мешков. Масса всего собранного картофеля – 480 кг. Найди массу картофеля, собранного с каждой грядки.» – задача на:
а) пропорциональное деление;
б) нахождение частного;
в) деление;
42. Задача «С одной грядки собрали 4 мешка картофеля, а с другой – 6 таких же мешков. Масса мешков, собранных со второй грядки, на 96 кг больше массы мешков, собранных с первой грядки. Сколько кг картофеля собрали с первой и со второй грядок в отдельности?» – задача на:
а) нахождение неизвестного по двум разностям;
б) нахождение частного;
в) деление;
43. Задача «Пешеход за 3 часа прошёл 15 км. В каждый час он проходил одинаковое расстояние. Сколько километров пешеход проходил в час?» – задача на:
а) движение;
б) нахождение частного;
в) деление;
44. Выберете верный порядок этапов работы над величинами:
а) Сравнение величин «на глаз», с помощью мускульных усилий. Введение единицы измерения величины и установление отношения между ними и ранее рассмотренными. Преобразование величин: крупные заменяются мелкими, а мелкие – крупными. Сравнение величин путём измерения. Операции над величинами.
б) Введение единицы измерения величины и установление отношения между ними и ранее рассмотренными. Сравнение величин «на глаз», с помощью мускульных усилий. Преобразование величин: крупные заменяются мелкими, а мелкие – крупными. Сравнение величин путём измерения. Операции над величинами.
в) Сравнение величин «на глаз», с помощью мускульных усилий. Введение единицы измерения величины и установление отношения между ними и ранее рассмотренными. Сравнение величин путём измерения. Преобразование величин: крупные заменяются мелкими, а мелкие – крупными. Операции над величинами.
45. Традиционным в начальной школе называют учебник математики авторов:
а) М.А.Бантовой и М.И.Моро;
б) Петерсон Л.Г.;
в) Истоминой Н.Б.;
46. Процесс обучения математике является…………….методики преподавания математики.
а) предметом
б) целью
в) задачей
47. Ядро методической системы обучения математике составляют цели, содержание,........................... обучения.
а) методы.
б) формы
в) приемы
48. Соответствие понятия и компонента содержания начального математического образования «дробные числа»
а) арифметический материал
б) величины
в) элементы геометрии
49. Соответствие понятия и компонента содержания начального математического образования
«площадь»
а) величины
б) элементы комбинаторики
в) элементы геометрии
50. Соответствие понятия и компонента содержания начального математического образования
«угол»
а) элементы геометрии
б) элементы комбинаторики
в) величины
51. Соответствие понятия и компонента содержания начального математического образования
«равенство»
а) элементы алгебры
б) элементы геометрии
в) величины
52. Данное суждение верно:
а) урок – основная форма обучения младших школьников математике;
б) основными методами обучения младших школьников математике являются наблюдение и эксперимент
в) к видам внеклассной работы относятся: домашняя работа учащихся, групповая работа, фронтальная работа;
53. Последовательность этапов урока «открытие» нового знания в структуре технологии деятельностного метода «Школа 2000…» (Л.Г. Петерсон):
А. постановка учебной задачи - Б. «открытие» нового знания - В. самостоятельная работа с самопроверкой - Г. первичное закрепление - Д. актуализация опорных знаний - Е. итог урока (рефлексия); - Ж. самоопределение к учебной деятельности; - З. включение в систему знаний и повторение.
а) ж, д, а, б, г, в, з, е.
б) д, б, а, г, в, е, з , ж.
в) ж, е, в, г, а, б, з, д .
54. Тип и структура урока математики в начальной школе определяются:
а) дидактическими задачами урока;
б) воспитательными задачами урока;
в) индивидуальными особенностями младших школьников;
55. Соответствие между этапом урока «открытия» нового знания и его дидактической целью- «открытие» нового знания
а) проектирование и фиксация нового знания
б) актуализация опорных знаний
в) изучение основного содержания учебной темы, формирование ЗУНов
56. Соответствие между этапом урока «открытия» нового знания и его дидактической целью: итог урока самооценки
а) рефлексия деятельности
б) формирование навыков самоконтроля
в) содержательная и мыслительная подготовка
57. Соответствие между этапом урока «открытия» нового знания и его дидактической целью: организационный момент
а) положительное самоопределение к учебной деятельности
б) рефлексия деятельности
в) формирование ЗУНов
58. Соответствие между этапом урока «открытия» нового знания и его дидактической целью: актуализация опорных знаний
а) содержательная и мыслительная подготовка
б) рефлексия деятельности
в) проектирование и фиксация нового знания
59. Соответствие между этапом урока «открытия» нового знания и его дидактической целью: повторение, создание затруднения в индивидуальной познавательной деятельности
а) включение нового знания в систему знаний
б) формирование навыков самоконтроля
в) рефлексия деятельности
60. Соответствие между этапом урока «открытия» нового знания и его дидактической целью: самостоятельная работа с самопроверкой деятельности
а) формирование навыков самоконтроля и
б) включение нового знания в систему знаний
в) содержательная и мыслительная подготовка,
7.5.3. Задания для оценки умений
БАЗОВЫЙ УРОВЕНЬ ПК-1-БУ
6.2.1.(ПК-1-БУ-1)
Какие ошибки допустил ученик при выполнении заданий в рабочей тетради для 1 класса М.М. Безруких, М.И. Кузнецовой, Е.Э. Кочуровой[5] (рис. 16, рис. 17)? В рабочей тетради для 1 класса В.Н. Рудницкой[6] (рис. 18). В чем причина ошибок? Каковы приемы работы с учеником?
Рис. 16 Рис. 17.

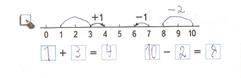
Рис. 18

6.2.2.(ПК-1-БУ-1)
Найдите в учебниках разных авторов задания, которые можно использовать для формирования табличных навыков сложения и соответствующих навыков вычитания в пределах 10, 20. Придумайте свои задания.
6.2.3.(ПК-1-БУ-2)
Найдите в учебниках разных авторов задания, которые можно использовать для формирования умения складывать и вычитать однозначные и двузначные числа без перехода в другой разряд.
6.2.4.(ПК-1-БУ-2)
Найдите в учебниках разных авторов задания, которые можно использовать для формирования умения складывать и вычитать однозначные и двузначные числа с переходом в другой разряд.
6.2.5.(ПК-1-БУ-3)
Проанализируйте приёмы изучения табличного умножения в учебниках разных авторов. Составьте несколько упражнений для формирования навыка табличного умножения и соответствующего навыка деления.
6.2.6.(ПК-1-БУ-3)
Воспроизведите алгоритм письменного сложения на примере задания: Вычисли значение суммы 123746 + 8502.
6.2. 7 . (ПК-1-БУ-4)
Воспроизведите алгоритм письменного вычитания на примере задания: Вычисли значение частного 37418 – 5579.
6.2. 8.(ПК-1-БУ-4)
Воспроизведите алгоритм письменного умножения на примере задания: Вычисли значение произведения 3215 · 740.
6.2. 9. (ПК-1-БУ-5)
Воспроизведите алгоритм письменного деления на примере задания: Вычисли значение частного 2712: 4.
6.2.10.(ПК-1-БУ-5)
Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного сложения.
6.2.11.(ПК-1-БУ-6)
Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного умножения.
6.2.12.(ПК-1-БУ-6)
Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного вычитания.
6.2.13.(ПК-1-БУ-7)
Составьте задания, которые можно предложить младшим школьникам для овладения алгоритмом письменного деления.
6.2.14. (ПК-1-БУ-7)
Придумайте задания, которые можно предложить ученикам для усвоения названий геометрических фигур.
6.2.15. (ПК-1-БУ-8)
Придумайте задания, которые можно предложить ученикам для усвоения сравнения геометрических фигур.
6.2.16. (ПК-1-БУ-8)
Придумайте задания, которые можно предложить ученикам для определения существенных свойств геометрических фигур.
6.2.17. (ПК-1-БУ-9)
Приведите рассуждения учащихся при решении уравнений:
х – 12 = 34 150: х = 50 5 · х – 10 = 290.
6.2.18.(ПК-1-БУ-9)
Рассмотри стр. 12-13 учебника математики для 1 класс Л.В. Занкова, В.В.Занкова. Какие виды заданий на формирование знаний о нумерации чисел первого десятка предлагается выполнить (рис.1).
Рис.1

6.2.19.(ПК-1-БУ-10)
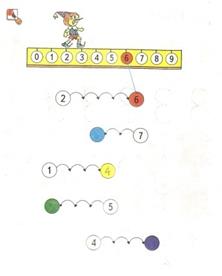
Рассмотри задание №50 на стр. 26 учебника для 1 класса Н.Б. Истоминой (Закрой «лишнюю» картинку в каждом ряду). Какие задачи обучения и развития позволяет реализовать выполнение этого задания? (рис. 2).
Рис.2

6.2.20 (ПК-1-БУ-10)
Какие образовательные задачи можно решить при выполнении задания, представленного на рис.4 из рабочей тетради для 1 класса М.М. Безруких, М.И. Кузнецовой, Е.Э. Кочуровой[7] .
Рис. 4
ПОВЫШЕННЫЙ УРОВЕНЬ ПК-1-ПУ
6.2.1. (ПК-1-ПУ-1)
Сделайте анализ предложенного фрагмента урока. Соответствуют ли предлагаемые на уроке задания задачам урока? Какие подходы используются для формирования знаний? Какими методами формируется знания о разрядных десятках? Какие средства обучения используются?
Фрагмент урока
Тема: Формирование понятия о разрядных десятках.
Задачи: Повторить нумерацию чисел первого десятка, учить считать разрядными десятками от 10 до 100, записывать разрядные десятки, сравнивать разрядные десятки между собой и с однозначными числами, формировать понятие о разряде, закрепить умения выполнять арифметические действия сложение и вычитание с числами первого десятка..
Устный счет:
6) Вставьте пропущенное число:
1, …, 3, 4, …, 6, …, …, 9, …; 10, 9, …, …, …, 5, 4, …, 2, …
7) Сравните числа. Вставьте нужный знак.
6 … 9; 5…2; 7…7
Напишите нужную цифру. Дайте несколько вариантов ответа, если это возможно.
3>…; 7<…; …>…; …= 6; …=….
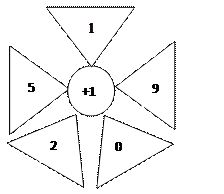
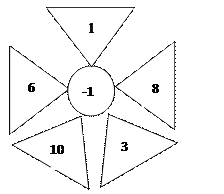
8) Реши (рис. 7)
Рис.7
9) Какие числа пропущены. Поднимите нужную карточку.
5 +…= 10; …+ 6 = 8; 7 - … = 4; … - 6 = 3
10) На катке катались девочки и мальчики. Девочек было 7, а мальчиков на 4 меньше, чем девочек. Сколько детей каталось на катке?
Актуализация знаний. Учитель предлагает положить перед собой на парту одну палочку и карточку с соответствующей цифрой; увеличить количество палочек на 1 и опять положить соответствующую карточку и т.д. до 10. Поясняет, что выполнялся счет единиц. Далее просит взять столько же пучков палочек, напоминает, что в одном пучке десять палочек и значит, будет выполняться счет десятков.
Усвоение новых знаний. Сегодня мы познакомимся с разрядными десятками. Пересчитаем десятки: один десяток, два десятка (и т.д.). Дадим каждому десятку свое название. Один десяток – десять, два десятка – двадцать (и т.д.). Счет десяток ведется так же, как счет единиц. При записи десятков используются такие же цифры, но записываются они на втором месте – в разряде десятков, а на первом месте, в разряде единиц стоит цифра 0. Это двузначные числа, в их записи два знака – цифры. Знак на первом месте, справа, показывает количество единиц, а знак на втором месте, слева, показывает количество десятков.
Оформление доски: (рис.8)
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
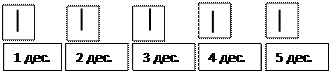 |  | 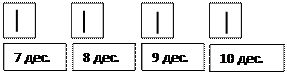 | |||










| | | | | ||||||||||||||||
| | | ||||||||||||||||||
| | | | | ||||||||||||||||
Формирование умений. Как вы думаете, что означает цифра 0 в записи разрядных десятков? Что означает цифра, стоящая на втором месте? Сколько цифр в записи разрядных десятков? Почему? Сколько десятков в числе 30, какая цифра стоит в разряде десятков. Какая цифра стоит в разряде единиц. Сколько в числе 30 единиц.
Работа по учебнику и в тетради. Конец фрагмента.
6.2.2. (ПК-1-ПУ-1)
На основании анализа вышеприведенного фрагмента урока дайте ответ на вопрос: Какие подходы используются для формирования знаний?
6.2.3. (ПК-1-ПУ-2)
На основании анализа вышеприведенного фрагмента урока дайте ответ на вопрос: Какими методами формируется знания о разрядных десятках?
6.2.4. (ПК-1-ПУ-2)
На основании анализа вышеприведенного фрагмента урока дайте ответ на вопрос: Какие средства обучения используются?
6.2. 5. (ПК-1-ПУ-3)
Сделайте сравнительный анализ подходов к изучению нумерации чисел второго десятка представленные в учебнике для 1 класса М.И. Моро и др. (рис.9) и в учебнике для 1 класса Л.В. Занкова, В.В. Занкова (рис. 10).
Рис. 9
. 

Рис. 10

6.2. 6. (ПК-1-ПУ-3)
Сделайте анализ предложенного фрагмента урока. Какие задачи урока реализованы в течение устного счета, какие еще предстоит реализовать?
Фрагмент урока
Тема: Замена числа суммой разрядных слагаемых.
Задачи: Учить раскладывать число на разрядные слагаемые и составлять число из разрядных слагаемых; закрепить умение читать и записывать числа первой тысячи, знания о поместном значении цифр в числе, соотношении разрядных чисел (каждые 10 единиц одного разряда составляет единицу следующего высшего разряда), о месте чисел первой тысячи в натуральном ряду; закрепить умения выполнять сравнение и арифметические действия с числами первой тысячи.
Устный счет:
7) Прочи
