По курсу «математика» (первый семестр)
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ПО КУРСУ «МАТЕМАТИКА» (ПЕРВЫЙ СЕМЕСТР)
Тула 2012
Рассмотрено и утверждено на заседании кафедры математического моделирования механико-математического факультета,
протокол № 11 от "21" июня 2011 г.
Данные методические указания написаны в помощь студентам технических специальностей для самостоятельной работы в первом семестре. Рассмотрены решения типовых задач по аналитической геометрии и линейной алгебре, введению в математический анализ, а также даны необходимые теоретические сведения и ссылки на литературу.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Теоретические сведения.
В прямоугольной декартовой системе координат Oxyz положение любой точки задается тремя числами – координатами : 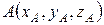 (рисунок 1).
(рисунок 1).
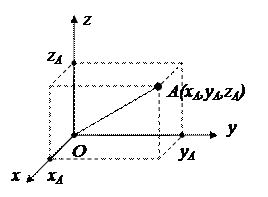
Рисунок 1.
Расстояние между двумя точками 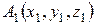 и
и 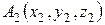 определяется по формуле
определяется по формуле
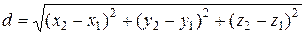 . (1)
. (1)
При решении задач аналитической геометрии на плоскости необходимы следующие сведения о прямой линии:
1) если точка М(x; y) делит отрезок М1М2 (М1(х1; у1) и М2(х2; у2)) в отношении λ, то координаты этой точки выражаются формулами
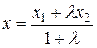 ,
, 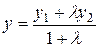 , (2)
, (2)
если же точка М(x; y) - середина отрезка М1М2, то
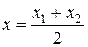 ,
, 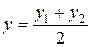 ; (3)
; (3)
2) уравнение прямой, проходящей через точку М1(x1; y1) и имеющей данный угловой коэффициент k, записывается в виде
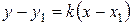 ; (4)
; (4)
3) уравнение прямой, проходящей через две данные точки М1(x1; y1) и М2(x2; y2), имеет вид
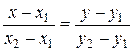 , при этом
, при этом 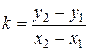 ; (5)
; (5)
4) острый угол между двумя прямыми с угловыми коэффициентами k1 и k2 определяется по формуле
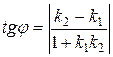 , (6)
, (6)
при этом условие параллельности прямых имеет вид k1=k2, а условие перпендикулярности 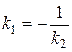 ; (7)
; (7)
5) если прямая на плоскости задана общим уравнением Ах+Ву+С=0, то 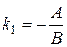 - ее угловой коэффициент;
- ее угловой коэффициент;
6) если в общем уравнении прямой поделить все члены на 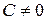 , получим уравнение прямой в отрезках:
, получим уравнение прямой в отрезках:
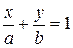 , где
, где 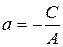 ,
, 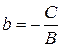 ; (8)
; (8)
7) точка пересечения двух прямых А1х+В1у+С1=0 и А2х+В2у+С2=0 определяется из решения системы уравнений
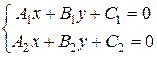 . (9)
. (9)
Уравнение окружности с центром в точке 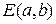 и радиусом R имеет вид
и радиусом R имеет вид
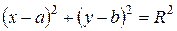 . (10)
. (10)
Пример выполнения задания.
| Даны вершины треугольника АВС: А(– 4;8), В(5; – 4), С(10;6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС в общем виде и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD в общем виде и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр. |
Решение:
1) Расстояние d между двумя точками на плоскости определяется по формуле (1), в которую подставлены значения координат точек А и В (положим 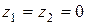 ), тогда
), тогда
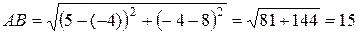 .
.
2) Уравнение прямой, проходящей через две заданные точки имеет вид (5):
Подставив в (5) координаты точек А и В, получим уравнение прямой АВ:
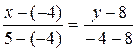 ,
, 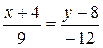 ,
, 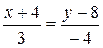 ,
,
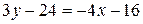 , или
, или 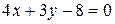 (АВ).
(АВ).
Для нахождения углового коэффициента kAB прямой АВ разрешим полученное уравнение относительно y: 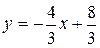 . Отсюда
. Отсюда 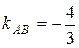 . Подставив в формулу (5) координаты точек А и С, найдем уравнение прямой АС:
. Подставив в формулу (5) координаты точек А и С, найдем уравнение прямой АС: 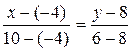 ,
, 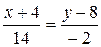 ,
, 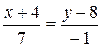 ,
,
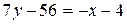 или x + 7y – 52 = 0 (AC).
или x + 7y – 52 = 0 (AC).
Отсюда 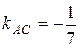 .
.
3) Угол между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле (6). Угол А, образованный прямыми АВ и АС, найдем по формуле (6), подставив в нее 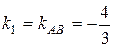 ,
, 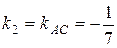 .
.
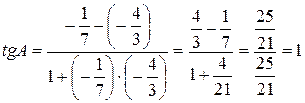 ,
,
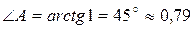 рад.
рад.
4) Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых связаны соотношением (7), поэтому
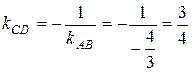 .
.
Уравнение прямой, проходящей через заданную точку в заданном угловым коэффициентом k направлении, имеет вид (4). Подставив в (4) координаты точки С и 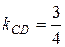 , получим уравнение высоты СD:
, получим уравнение высоты СD:
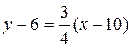 ,
, 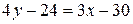 ,
, 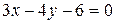 (CD).
(CD).
Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (СD):
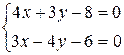 , откуда х = 2, y = 0, то есть D (2;0).
, откуда х = 2, y = 0, то есть D (2;0).
Подставив в формулу (1) координаты точек С и D, находим:
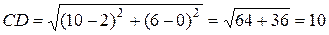 .
.
5) Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулой (3) деления отрезка пополам, получим:
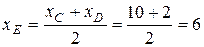 ,
, 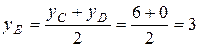 .
.
Следовательно, Е (6; 3) и 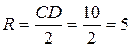 . Используя формулу (10), получаем уравнение искомой окружности: (х – 6)2+( y – 3)2 = 25.
. Используя формулу (10), получаем уравнение искомой окружности: (х – 6)2+( y – 3)2 = 25.
Задача 2.
Теоретические сведения.
Если известны начало вектора 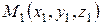 и конец
и конец 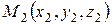 , то координаты вектора
, то координаты вектора 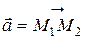 находятся по формулам
находятся по формулам
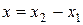 ,
, 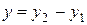 ,
, 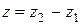 , (11)
, (11)
а его длина определяется выражением
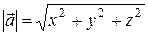 . (12)
. (12)
Вектор 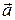 с координатами
с координатами 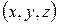 может быть представлен разложением по ортам в виде
может быть представлен разложением по ортам в виде
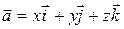 . (13)
. (13)
Если α, β, γ – углы, которые вектор 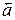 образует с положительными направлениями осей координат, то cosα, cosβ, cosγ называются направляющими косинусами вектора
образует с положительными направлениями осей координат, то cosα, cosβ, cosγ называются направляющими косинусами вектора 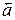 (рисунок 2). Тогда имеют место соотношения
(рисунок 2). Тогда имеют место соотношения
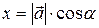 ,
, 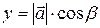 ,
, 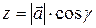 ,
, 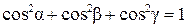 .
.
Для векторов 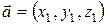 и
и 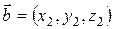 вводятся операции сложения и умножения на число такие, что
вводятся операции сложения и умножения на число такие, что
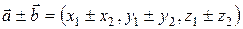 и
и 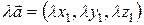 ,
,
где 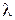 − любое число.
− любое число.
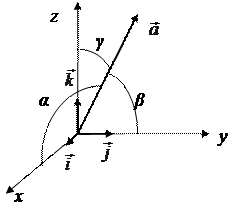
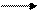 Рисунок 2.
Рисунок 2.
Скалярным произведением двух векторов 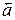 и
и 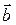
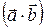 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 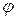 между ними,
между ними, 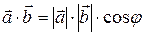 или, если векторы заданы своими координатами, то
или, если векторы заданы своими координатами, то
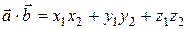 . (14)
. (14)
Векторы, лежащие на одной или параллельных прямых, называют коллинеарными. Признак коллинеарности векторов 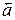 и
и 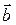 является пропорциональность их координат:
является пропорциональность их координат:
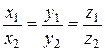 . (15)
. (15)
Если векторы 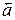 и
и 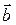 взаимно перпендикулярны, то
взаимно перпендикулярны, то 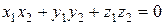 . Угол между векторами
. Угол между векторами 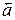 и
и 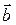 определяется соотношением:
определяется соотношением:
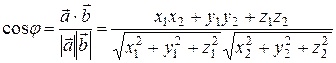 . (16)
. (16)
Уравнение плоскости, проходящей через точку 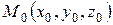 перпендикулярно вектору
перпендикулярно вектору 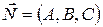 , имеет вид
, имеет вид
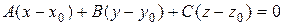 . (17)
. (17)
Пример выполнения задания.
Даны координаты трех точек: А(3; 0; –5), В(6; 2; 1), С(12; –12; 3). Требуется: 1) записать векторы 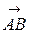 и и 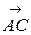 в системе орт и найти модули этих векторов; 2) найти угол между векторами в системе орт и найти модули этих векторов; 2) найти угол между векторами 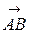 и и 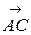 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 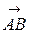 . . |
Решение:
1) Найдем координаты вектора 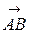 , подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
, подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
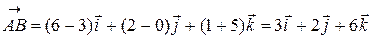 .
.
Подобным образом
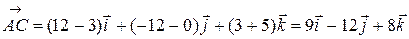 .
.
Модули векторов 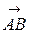 и
и 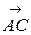 найдем, подставляя их координаты в формулу (12):
найдем, подставляя их координаты в формулу (12):
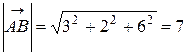 ,
, 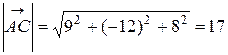 .
.
2) Найдем косинус угла φ между векторами 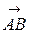 и
и 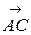 . Для этого вычислим их скалярное произведение по формуле (14):
. Для этого вычислим их скалярное произведение по формуле (14):
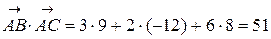 .
.
Тогда по формуле (16)
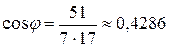 , φ ≈ 64˚37΄ ≈1,13 рад.
, φ ≈ 64˚37΄ ≈1,13 рад.
3) По условию задачи искомая плоскость проходит через точку С(12; –12; 3) перпендикулярно вектору 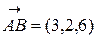 . Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
. Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
3(х – 12) +2 (y + 12) + 6(z – 3) = 0,
или 3х + 2у + 6z – 30 = 0 – искомое уравнение плоскости.
Задача 3.
Теоретические сведения.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Условием компланарности трех векторов 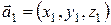 ,
, 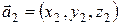 ,
, 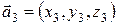 является равенство нулю их смешанного произведения:
является равенство нулю их смешанного произведения:
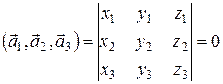 . (18)
. (18)
Три вектора образуют базис в том случае, если они некомпланарны.
Если для векторов 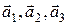 выполняется условие
выполняется условие 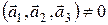 , то они образуют базис, и любой четвертый вектор
, то они образуют базис, и любой четвертый вектор 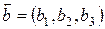 может быть представлен разложением по этому базису в виде
может быть представлен разложением по этому базису в виде
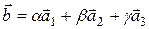 , (19)
, (19)
где α, β, γ – координаты вектора 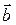 в базисе, образованном векторами
в базисе, образованном векторами 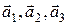 .
.
Координаты α, β, γ находятся из системы уравнений:
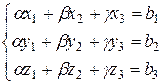 . (20)
. (20)
Пример выполнения задания.
Показать, что векторы 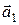 (3; 1; 4), (3; 1; 4), 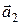 (2; 1; –1), (2; 1; –1), 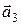 (1; –1; 5) образуют базис трехмерного пространства. Найти координаты вектора (1; –1; 5) образуют базис трехмерного пространства. Найти координаты вектора 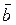 (5; 0; 3) в этом базисе. (5; 0; 3) в этом базисе. |
Решение:
Вычислим смешанное произведение векторов 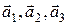 :
:
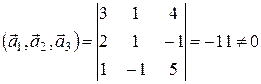 .
.
Так как смешанное произведение отлично от нуля, то векторы некомпланарны и образуют базис. Координаты вектора 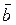 в этом базисе найдем, разложив его по векторам
в этом базисе найдем, разложив его по векторам 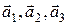 следующим образом:
следующим образом:
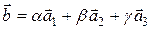 ,
,
а координаты вектора 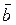 в новом базисе найдем из системы уравнений (20)
в новом базисе найдем из системы уравнений (20)
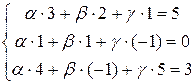 или
или 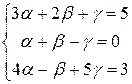
Решим эту систему для заданных векторов методом Гаусса.
Поменяем местами первое и второе уравнения
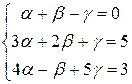 .
.
После этого умножим первое уравнение на (–3) и сложим со вторым. Далее умножим первое уравнение на (–4) и сложим с третьим. Получим:
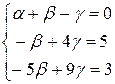 .
.
Затем умножаем второе уравнение на (−5) и складываем с третьим:
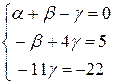 .
.
Из последнего уравнения имеем γ= 2. Подставляем это значение во второе уравнение, получаем β= 3 и, наконец, из первого уравнения находим α= –1.
Таким образом, подставив в уравнение (19) координаты вектора 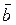 , получим
, получим
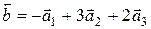 .
.
Задача 4.
Теоретические сведения.
Неоднородная система трех уравнений с тремя неизвестными в общем случае имеет вид
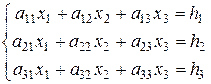
и может быть записана в матричном виде
А·Х = Н, (21)
где 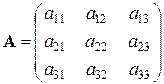 -матрица коэффициентов при неизвестных,
-матрица коэффициентов при неизвестных,
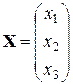 - матрица-столбец неизвестных,
- матрица-столбец неизвестных,
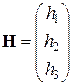 матрица-столбец свободных членов.
матрица-столбец свободных членов.
Если матрица А – невырожденная, то есть имеет определитель, отличный от нуля, то существует матрица А-1, обратная к А, так что А-1·А=Е (Е - единичная матрица). Умножим обе части уравнения (22) на А-1 и получим
А-1·А·Х =А-1· Н,
или
Х =А-1· Н, (23)
поскольку А-1·А·Х=Е·Х=Х.
Равенство (23) является решением системы уравнений (22).
Матрица, обратная к невырожденной матрице А, находится по формуле
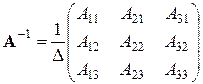 , (24)
, (24)
где Аіј (i = 1, 2, 3; j = 1, 2, 3) – алгебраическое дополнение элемента аij, которое является произведением (-1)i+j на минор (определитель) второго порядка, полученный вычеркиваем i-й строки и j-го столбца в определителе матрицы А; Δ – определитель матрицы А.
Пример выполнения задания.
Данную систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы: 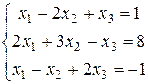 |
Решение:
Выпишем для данной системы уравнений матрицу коэффициентов при неизвестных А и столбец свободных членов Н:
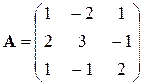 ,
, 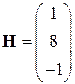 .
.
Вычислим определитель Δ и алгебраические дополнения Аіј элементов матрицы А:
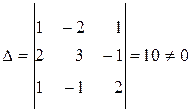 ,
,
следовательно, матрица А имеет обратную матрицу А-1.
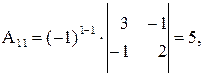
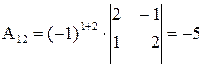 ,
, 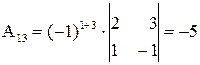 ,
,
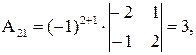
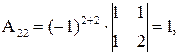
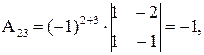
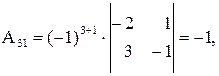
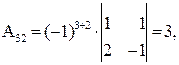
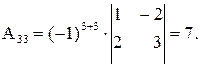
Тогда по формуле (24) обратная матрица равна
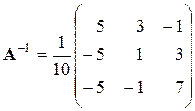 .
.
По формуле (23) находим решение данной системы уравнений в матричной форме:
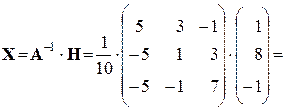
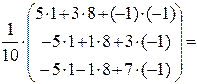
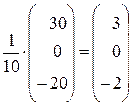 .
.
Отсюда х1= 3, х2= 0, х3= −2.
Задача 5.
Теоретические сведения.
Число A называют пределом функции y=f(x) в точке a , если эта функция определена в некоторой окрестности точки a , за исключением, быть может, самой точки a , и для каждого e>0 найдется такое d>0, что для всех x, удовлетворяющих условию 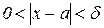 , выполняется неравенство
, выполняется неравенство 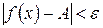 :
:
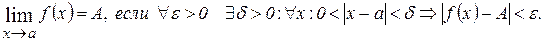
Вычисление пределов арифметических выражений 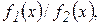
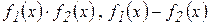 по пределам функций
по пределам функций 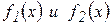 , из которых они составлены, не всегда возможно. В этих случаях говорят, что возникают неопределенности следующих видов:
, из которых они составлены, не всегда возможно. В этих случаях говорят, что возникают неопределенности следующих видов:
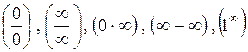 .
.
Для нахождения пределов таких неопределенных выражений нужно
учитывать конкретный вид функции 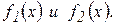 Например,
Например,
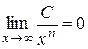 ; (25)
; (25)
предел отношения двух многочленов 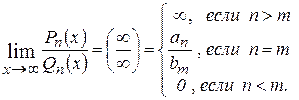 ;
;
первый замечательный предел 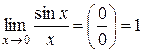 ; (26)
; (26)
второй замечательный предел 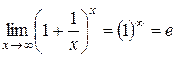 . (27)
. (27)
Величина 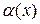 называется бесконечно малой при
называется бесконечно малой при 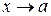 , если
, если 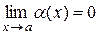 . Две бесконечно малые величины называются эквивалентными, если предел их отношения равен 1, то есть
. Две бесконечно малые величины называются эквивалентными, если предел их отношения равен 1, то есть 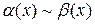 , если
, если 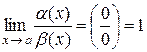 . Под знаком предела любая бесконечно малая величина может быть заменена на эквивалентную ей. Приведем таблицу эквивалентных бесконечно малых при
. Под знаком предела любая бесконечно малая величина может быть заменена на эквивалентную ей. Приведем таблицу эквивалентных бесконечно малых при 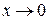 величин:
величин:
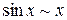 ,
, 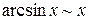 ,
, 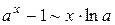
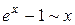 ,
,
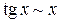 ,
, 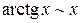 ,
, 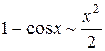 . (28)
. (28)
Пример выполнения задания.
Вычислить пределы: а) 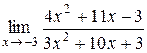 , б) , б) 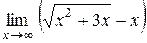 , в) , в) 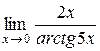 ,г) ,г) 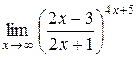 . . |
Решение:
а) Подстановка предельного значения аргумента х=-3 приводит к неопределенному выражению вида 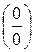 .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при х→ −3:
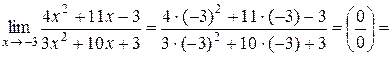
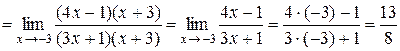 .
.
б) При х→ ∞ выражение 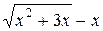 дает неопределенность вида (∞ − ∞). Для ее устранения умножим и разделим это выражение на
дает неопределенность вида (∞ − ∞). Для ее устранения умножим и разделим это выражение на 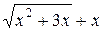 , после чего разделим числитель и знаменатель полученной дроби на х , учитывая формулу (25):
, после чего разделим числитель и знаменатель полученной дроби на х , учитывая формулу (25):
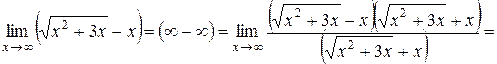
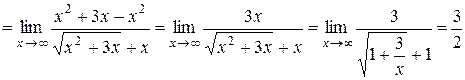 .
.
в) При 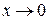 получим неопределенность
получим неопределенность 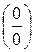 . Обозначим arctg5x = y. Тогда 5х=tgy и y → 0 при х → 0. Применяя свойства пределов и формулу (26), имеем:
. Обозначим arctg5x = y. Тогда 5х=tgy и y → 0 при х → 0. Применяя свойства пределов и формулу (26), имеем:
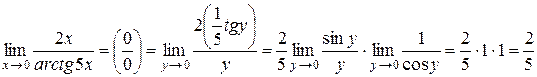 .
.
Эту задачу можно решить, используя эквивалентные замены бесконечно малых величин (28). Поскольку при 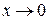 эквивалентны
эквивалентны 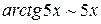 , можно записать
, можно записать
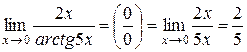 .
.
г) При 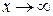 выражение
выражение 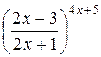 является неопределенностью вида
является неопределенностью вида 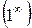 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой (при х → ∞) величины; после чего применим формулу второго замечательного предела (27):
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой (при х → ∞) величины; после чего применим формулу второго замечательного предела (27):
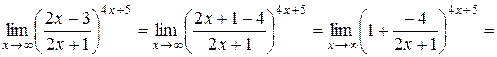
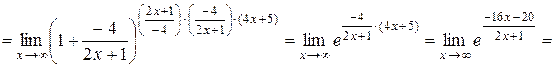
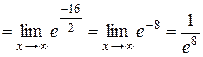 .
.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1 Основная литература
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры : Учебник для вузов / Д.В.Беклемишев .— 9-е изд., испр. — М.: Физматлит, 2002 .— 376с.
2. Ильин В.А., Аналитическая геометрия : учебник для вузов / В.А.Ильин, Э.Г.Позняк .— 6-е изд.,стер. — М. : Физматлит, 2002 .— 240с.
3. Клетеник Д.В. Сборник задач по аналитической геометрии: учебное пособие для втузов / под ред. Н.В.Ефимова .— 17-е изд., стер. — СПб. : Профессия, 2004 .— 200с.
4. Кузнецов Л.А. Сборник заданий по высшей математике: Типовые расчеты : учеб. пособие / Л. А. Кузнецов .— 9-е изд., стер .— СПб. [и др.] : Лань, 2007 .— 240 с.
5. Бермант А.Ф. Краткий курс математического анализа : учеб. пособие для вузов / А. Ф. Бермант, И. Г. Араманович .— 14-е изд., стер. — СПб. ; М. ; Краснодар : Лань, 2008 .— 736 с.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления : учеб. пособие для втузов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ПО КУРСУ «МАТЕМАТИКА» (ПЕРВЫЙ СЕМЕСТР)
Тула 2012
Рассмотрено и утверждено на заседании кафедры математического моделирования механико-математического факультета,
протокол № 11 от "21" июня 2011 г.
Данные методические указания написаны в помощь студентам технических специальностей для самостоятельной работы в первом семестре. Рассмотрены решения типовых задач по аналитической геометрии и линейной алгебре, введению в математический анализ, а также даны необходимые теоретические сведения и ссылки на литературу.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.
Теоретические сведения.
В прямоугольной декартовой системе координат Oxyz положение любой точки задается тремя числами – координатами : 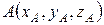 (рисунок 1).
(рисунок 1).
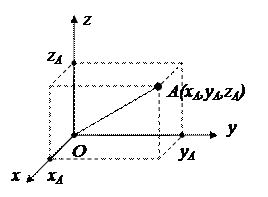
Рисунок 1.
Расстояние между двумя точками 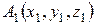 и
и 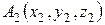 определяется по формуле
определяется по формуле
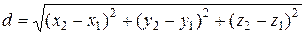 . (1)
. (1)
При решении задач аналитической геометрии на плоскости необходимы следующие сведения о прямой линии:
1) если точка М(x; y) делит отрезок М1М2 (М1(х1; у1) и М2(х2; у2)) в отношении λ, то координаты этой точки выражаются формулами
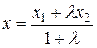 ,
, 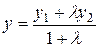 , (2)
, (2)
если же точка М(x; y) - середина отрезка М1М2, то
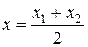 ,
, 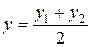 ; (3)
; (3)
2) уравнение прямой, проходящей через точку М1(x1; y1) и имеющей данный угловой коэффициент k, записывается в виде
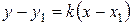 ; (4)
; (4)
3) уравнение прямой, проходящей через две данные точки М1(x1; y1) и М2(x2; y2), имеет вид
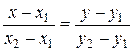 , при этом
, при этом 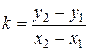 ; (5)
; (5)
4) острый угол между двумя прямыми с угловыми коэффициентами k1 и k2 определяется по формуле
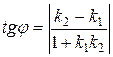 , (6)
, (6)
при этом условие параллельности прямых имеет вид k1=k2, а условие перпендикулярности 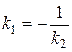 ; (7)
; (7)
5) если прямая на плоскости задана общим уравнением Ах+Ву+С=0, то 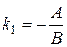 - ее угловой коэффициент;
- ее угловой коэффициент;
6) если в общем уравнении прямой поделить все члены на 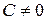 , получим уравнение прямой в отрезках:
, получим уравнение прямой в отрезках:
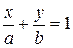 , где
, где 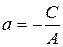 ,
, 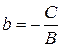 ; (8)
; (8)
7) точка пересечения двух прямых А1х+В1у+С1=0 и А2х+В2у+С2=0 определяется из решения системы уравнений
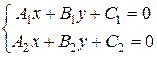 . (9)
. (9)
Уравнение окружности с центром в точке 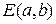 и радиусом R имеет вид
и радиусом R имеет вид
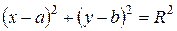 . (10)
. (10)
Пример выполнения задания.
| Даны вершины треугольника АВС: А(– 4;8), В(5; – 4), С(10;6). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС в общем виде и их угловые коэффициенты; 3) внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты СD в общем виде и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр. |
Решение:
1) Расстояние d между двумя точками на плоскости определяется по формуле (1), в которую подставлены значения координат точек А и В (положим 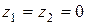 ), тогда
), тогда
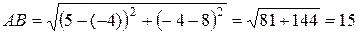 .
.
2) Уравнение прямой, проходящей через две заданные точки имеет вид (5):
Подставив в (5) координаты точек А и В, получим уравнение прямой АВ:
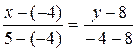 ,
, 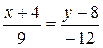 ,
, 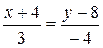 ,
,
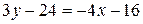 , или
, или 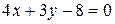 (АВ).
(АВ).
Для нахождения углового коэффициента kAB прямой АВ разрешим полученное уравнение относительно y: 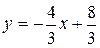 . Отсюда
. Отсюда 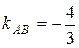 . Подставив в формулу (5) координаты точек А и С, найдем уравнение прямой АС:
. Подставив в формулу (5) координаты точек А и С, найдем уравнение прямой АС: 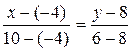 ,
, 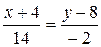 ,
, 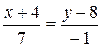 ,
,
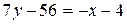 или x + 7y – 52 = 0 (AC).
или x + 7y – 52 = 0 (AC).
Отсюда 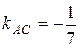 .
.
3) Угол между двумя прямыми, угловые коэффициенты которых равны k1 и k2, определяется по формуле (6). Угол А, образованный прямыми АВ и АС, найдем по формуле (6), подставив в нее 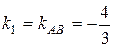 ,
, 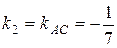 .
.
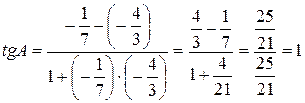 ,
,
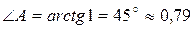 рад.
рад.
4) Так как высота CD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых связаны соотношением (7), поэтому
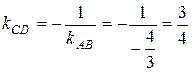 .
.
Уравнение прямой, проходящей через заданную точку в заданном угловым коэффициентом k направлении, имеет вид (4). Подставив в (4) координаты точки С и 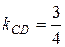 , получим уравнение высоты СD:
, получим уравнение высоты СD:
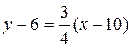 ,
, 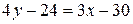 ,
, 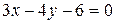 (CD).
(CD).
Для нахождения длины CD определим координаты точки D, решив систему уравнений (АВ) и (СD):
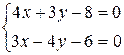 , откуда х = 2, y = 0, то есть D (2;0).
, откуда х = 2, y = 0, то есть D (2;0).
Подставив в формулу (1) координаты точек С и D, находим:
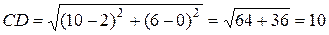 .
.
5) Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулой (3) деления отрезка пополам, получим:
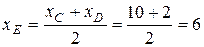 ,
, 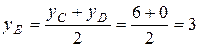 .
.
Следовательно, Е (6; 3) и 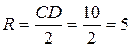 . Используя формулу (10), получаем уравнение искомой окружности: (х – 6)2+( y – 3)2 = 25.
. Используя формулу (10), получаем уравнение искомой окружности: (х – 6)2+( y – 3)2 = 25.
Задача 2.
Теоретические сведения.
Если известны начало вектора 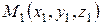 и конец
и конец 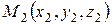 , то координаты вектора
, то координаты вектора 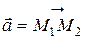 находятся по формулам
находятся по формулам
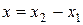 ,
, 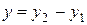 ,
, 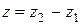 , (11)
, (11)
а его длина определяется выражением
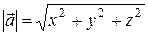 . (12)
. (12)
Вектор 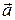 с координатами
с координатами 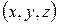 может быть представлен разложением по ортам в виде
может быть представлен разложением по ортам в виде
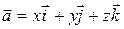 . (13)
. (13)
Если α, β, γ – углы, которые вектор 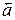 образует с положительными направлениями осей координат, то cosα, cosβ, cosγ называются направляющими косинусами вектора
образует с положительными направлениями осей координат, то cosα, cosβ, cosγ называются направляющими косинусами вектора 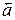 (рисунок 2). Тогда имеют место соотношения
(рисунок 2). Тогда имеют место соотношения
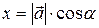 ,
, 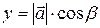 ,
, 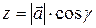 ,
, 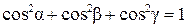 .
.
Для векторов 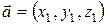 и
и 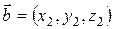 вводятся операции сложения и умножения на число такие, что
вводятся операции сложения и умножения на число такие, что
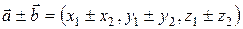 и
и 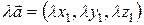 ,
,
где 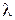 − любое число.
− любое число.

 Рисунок 2.
Рисунок 2.
Скалярным произведением двух векторов 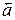 и
и 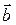
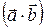 называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла 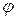 между ними,
между ними, 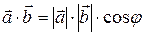 или, если векторы заданы своими координатами, то
или, если векторы заданы своими координатами, то
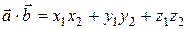 . (14)
. (14)
Векторы, лежащие на одной или параллельных прямых, называют коллинеарными. Признак коллинеарности векторов 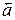 и
и 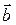 является пропорциональность их координат:
является пропорциональность их координат:
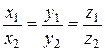 . (15)
. (15)
Если векторы 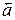 и
и 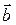 взаимно перпендикулярны, то
взаимно перпендикулярны, то 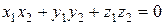 . Угол между векторами
. Угол между векторами 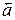 и
и 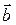 определяется соотношением:
определяется соотношением:
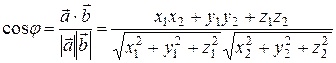 . (16)
. (16)
Уравнение плоскости, проходящей через точку 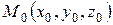 перпендикулярно вектору
перпендикулярно вектору 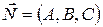 , имеет вид
, имеет вид
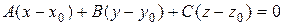 . (17)
. (17)
Пример выполнения задания.
Даны координаты трех точек: А(3; 0; –5), В(6; 2; 1), С(12; –12; 3). Требуется: 1) записать векторы 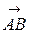 и и 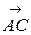 в системе орт и найти модули этих векторов; 2) найти угол между векторами в системе орт и найти модули этих векторов; 2) найти угол между векторами 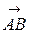 и и 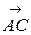 ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору 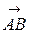 . . |
Решение:
1) Найдем координаты вектора 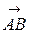 , подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
, подставив в формулу (11) координаты точек А и В, и запишем разложение этого вектора по ортам (13):
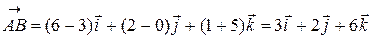 .
.
Подобным образом
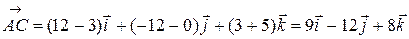 .
.
Модули векторов 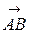 и
и 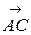 найдем, подставляя их координаты в формулу (12):
найдем, подставляя их координаты в формулу (12):
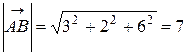 ,
, 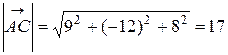 .
.
2) Найдем косинус угла φ между векторами 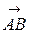 и
и 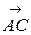 . Для этого вычислим их скалярное произведение по формуле (14):
. Для этого вычислим их скалярное произведение по формуле (14):
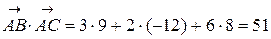 .
.
Тогда по формуле (16)
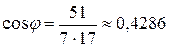 , φ ≈ 64˚37΄ ≈1,13 рад.
, φ ≈ 64˚37΄ ≈1,13 рад.
3) По условию задачи искомая плоскость проходит через точку С(12; –12; 3) перпендикулярно вектору 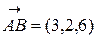 . Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
. Подставляя в (17) А= 3, В= 2, С= 6, х0= 12, у0= −12, z0= 3, получим:
3(х – 12) +2 (y + 12) + 6(z – 3) = 0,
или 3х + 2у + 6z – 30 = 0 – искомое уравнение плоскост
