Основные равносильности булевых формул.
Для любых формул A, B, C справедливы следующие равносильности:
1. Коммутативность.
а) A&B= B&A (для конъюнкции);
б) AÚB = BÚA (для дизъюнкции).
2. Ассоциативность.
а) A&(B&C) = (A&C)&C (для конъюнкции);
б) AÚ (BÚC) = (AÚB) ÚC (для дизъюнкции).
3. Дистрибутивность.
а) A&(BÚC) = A&BÚA&C (для конъюнкции относительно дизъюнкции);
б) AÚ (B&C) = (AÚB)&(AÚC) (для дизъюнкции относительно конъюнкции).
4. Закон де Моргана.
а) ù (A&B)= ù AÚù B (отрицание конъюнкции есть дизъюнкция отрицаний);
б) ù (AÚB)= ù A&ù B (отрицание дизъюнкции есть конъюнкция отрицаний).
5. Идемпотентность.
а) A&A = A (для конъюнкции);
б) AÚA = A (для дизъюнкции).
6. Поглощение.
а) A&(AÚB) = A (1– ый закон поглощения);
б) AÚA&B = A (2– ой закон поглощения).
7. Расщепление (склеивание).
а) A&B Ú A&ù B = A (1–ый закон расщепления);
б) (AÚB) & (AÚù B) = A (2–ой закон расщепления).
8. Двойное отрицание.
ù (ù A) = A.
9. Свойства констант.
а)A&1 = A; б) A&0 = 0; в)AÚ1 = 1; г) AÚ0 = A; д) ù 0= 1; е) ù 1= 0.
10. Закон противоречия.
A&ù A = 0.
11. Закон “исключенного третьего”.
AÚù A = 1.
Каждая из перечисленных равносильностей может быть доказана с помощью таблиц значений функций, составленных для выражений, стоящих слева и справа от символа “=”.
Следующие важные равносильности показывают, что все логические операции могут быть выражены через операции конъюнкции, дизъюнкции и отрицания:
12. A ®B =ù AÚB =ù (A&ù B).
13. A ~ B = (A®B)&(B®A) = (A&B) Ú (ù A&ù B) .
14. A 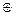 В=(A&ù B) Ú (ù A&B).
В=(A&ù B) Ú (ù A&B).
15. A¯B =ù (AÚB) =ù A&ù B.
16. AïB =ù (A&B) =ù AÚù B.
Двойственность. Принцип двойственности
Символы &, Ú называются двойственными.
Формула А* называется двойственной формуле A, если она получена из A одновременной заменой всех символов &, Ú на двойственные.
Пример 5.3. Для A = xÚ (y&ù z) двойственной будет A* = x & (yÚù z).
Теорема. (Принцип двойственности). Если A =B, то A* = B*.
Принцип двойственности можно использовать для нахождения новых равносильностей.
Пример 5.4. Для 1-го закона поглощения (равносильность 6а) имеем: A&(AÚB) = A. Следуя принципу двойственности, получим новую равносильность: AÚA&B = A (2- ой закон поглощения).
Нормальные формы
Элементарной конъюнкцией называется конъюнкция (возможно одночленная), составленная из переменных или отрицаний переменных.
Пример 5.5. x, y, x&y, ù x1&x2&(ù x3) – элементарные конъюнкции.
xÚy, x1&ù x2 Úù x1&x2 – не элементарные конъюнкции.
Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая вид дизъюнкции элементарных конъюнкций (в вырожденном случае это может быть одна конъюнкция).
Пример 5.6. x, x Ú ù x&(ù y), ù x1&x2& x3 Ú x1&(ù x2)&x3 Ú x1&x2&(ù x3) – ДНФ. (xÚy)& ù x – не ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, каждый конъюнктивный член которой содержит все переменные, либо их отрицания.
Пример 5.7. x&y, x&ù y Ú ù x&y Ú ù x&ù y – СДНФ функции двух переменных. xÚù x&y, xÚy – не СДНФ.
Элементарной дизъюнкцией называется дизъюнкция (возможно одночленная), составленная из переменных или отрицаний переменных.
Пример 5.8. x, y, xÚy, ù x1Úx2Ú (ù x3) – элементарные дизъюнкции.
x&y, (x1Úù x2) & (ù x1Úx2) – не элементарные дизъюнкции.
Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид конъюнкции элементарных дизъюнкций (в вырожденном случае это может быть одна дизъюнкция).
Пример 5.9. x, x&y, x & ù x&(ù y), (ù x1Úx2)&( ù x3)&(x1Úù x2Úx3) – КНФ.
x&y Ú ù x – не КНФ.
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая конъюнктивная нормальная форма, каждый дизъюнктивный член которой содержит все переменные, либо их отрицания.
Пример 5.10. xÚy, (xÚù y) &(ù xÚy) – СКНФ функции двух переменных.
x &(ù xÚy), x&y – не СКНФ.
Приведение некоторой формулы к ДНФ и КНФ не является однозначным. Количество равносильных ДНФ и КНФ, вообще говоря, бесконечно. Однако, совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ и СКНФ) или не существуют или единственны.
Теорема. Каждая формула A, не равная тождественно нулю, может быть приведена к СДНФ, которая является единственной с точностью до перестановки дизъюнктивных членов.
Теорема. Каждая формула A, не равная тождественно единице, может быть приведена к СКНФ, которая является единственной с точностью до перестановки конъюнктивных членов.
Примеры тестовых заданий
ЗАДАНИЕ N 5.1 ( - выберите один вариант ответа)
Необходимым и достаточным условием делимости натурального числа  на 24 является …
на 24 является …
ВАРИАНТЫ ОТВЕТОВ:
1) число a делится на 4 и на 6 2) число а делится на 2, на 3 и на 4
3) число a делится на 2 и на 12 4) число a делится на 3 и на 8
Решение. Необходимое и достаточное условие является равносильностью. Все перечисленные варианты ответов являются необходимыми условиями делимости на 24. Но условиям для 1-го, 2-го и 3-го вариантов удовлетворяет, например, число 36, но оно не делится нацело на 24. в то же время 24=3∙8, при этом 8 не имеет общих делителей с числом 3 , следовательно верный ответ: 4).
ЗАДАНИЕ N 5.2 ( - выберите несколько вариантов ответа)
Обозначим утверждение «четырехугольник является ромбом» через А, утверждение «диагонали четырехугольника перпендикулярны» через В. Тогда в теореме «диагонали ромба перпендикулярны» условие …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | А достаточно для В | 2) | В необходимо для А | |
| 3) | В достаточно для А | 4) | А необходимо для В |
Решение. В терминах алгебры логики рассматриваемое утверждение имеет вид: «если А, то В», это значит, что А достаточно для В и что В необходимо для А (см. п. 5.1). Верные ответы: 1) и 2).
ЗАДАНИЕ N 5.3 (- выберите один вариант ответа)
Укажите правильную таблицу истинности логического высказывания a Ù b…
ВАРИАНТЫ ОТВЕТОВ:
| 1) |
| 2) |
| 3) |
| 4) |
|
Решение. Логическое высказывание a Ù b – конъюнкция a и b, которая истинна (равна 1) тогда и только тогда, когда a и b истинны, т.е. равны 1. Верный ответ: 3).
ЗАДАНИЕ N 5.4 (- выберите один вариант ответа)
Укажите правильную таблицу истинности логического высказывания  Ú b…
Ú b…
ВАРИАНТЫ ОТВЕТОВ:
| 1) |
| 2) |
| 3) |
| 4) |
|
Решение. Логическое высказывание  Ú b – дизъюнкция
Ú b – дизъюнкция  и b, которая ложна (равна 0) тогда и только тогда, когда
и b, которая ложна (равна 0) тогда и только тогда, когда  и b ложны, т.е. а истинно (равно 1) а b ложно (равно 0). Верный ответ: 4).
и b ложны, т.е. а истинно (равно 1) а b ложно (равно 0). Верный ответ: 4).
ЗАДАНИЕ N 5.5 ( - выберите один вариант ответа)
Формула, реализующая функцию двойственную к функции  , имеет вид:
, имеет вид:
ВАРИАНТЫ ОТВЕТОВ:
| 1) |  | 2) |  | |
| 3) |  | 4) |  |
Решение. Заменяя в заданной функции дизъюнкции (Ú) на конъюнкции (Ù), а конъюнкции на дизъюнкции, получаем функцию, двойственную в данной:
g(x)=x Ú (y Ù z).
Учитывая то, что сначала выполняется конъюнкция, а затем дизъюнкция, скобки можно опустить, поэтому g(x)=x Ú y Ù z. Верный ответ 3).
Список литературы
1. Акимов О.Е. Дискретная математика: логика, группы, графы. – М.: Лаборатория Базовых Знаний, 2003. – 376 с.
2. Виленкин Н.Я. Комбинаторика. – М.: Наука, 1969 г., 328 с.
3. Канцедал С.А. Дискретная математика. – М.: «ФОРУМ»: ИНФРА-М; 2007, 224 с.
4. Кузьмин О.В. Перечислительная математика. – М.: Дрофа, 2005. – 110 с.
5. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и задачах. – М.: Логос, 2003. – 240 с.
6. Соболева Т.С., Чечкин А.В. Дискретная математика. - М.: Академия, 2006. - 256 с.
7. Судоплатов С.В., Овчинникова Е.В. Дискретная математика. – М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2009, 256 с.
Содержание
Введение. 3
1. Элементы теории множеств. 4
1.1. Множества и его элементы.. 4
1.2. Операции над множествами. 6
1.3. Декартово произведение множеств. 8
1.4. Алгебра множеств. 9
Примеры тестовых заданий. 11
2. Отображения. Отношения. 13
2.1. Отображение множеств. 13
2.2.Эквивалентность множеств. Мощность множества. 14
2.3. Бинарные отношения. 15
2.4. Свойства отношений. 17
Примеры тестовых заданий. 20
3. Комбинаторика. 22
3.1. Правило суммы. Правило произведения. 22
3.2. Перестановки. 24
3.3. Размещения. 24
3.4. Сочетания. 25
Примеры тестовых заданий. 26
4. Графы.. 27
4.1. Основные характеристики графов. 27
4.2. Матричные способы задания графов. 29
4.3. Изоморфизм графов. 30
4.4. Маршруты, циклы в неориентированном графе. 31
4.5. Пути, контуры в ориентированном графе. 32
4.6. Связность. Матрицы достижимости и связности. 33
4.7. Деревья. 34
Примеры тестовых заданий. 35
5. Алгебра логики. Исчисление высказываний.. 38
5.1. Формулы алгебры логики. 38
5.2. Функции алгебры логики. 40
5.3. Эквивалентность формул. 40
5.4. Двойственность. Принцип двойственности. 42
5.5. Нормальные формы.. 42
Примеры тестовых заданий. 44
Список литературы.. 46
