Связность. матрицы достижимости и связности
Говорят, что вершина w графа (орграфа) G достижима из вершины v, если либо w=v, либо существует маршрут (путь) из v в w.
Граф (орграф) называется связным (сильно связным), если для любых двух его вершин v, w существует маршрут (путь), соединяющий v и w.
Компонентой связности графа (сильной связности орграфа) G называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (ориентированного графа G).
Пусть А=A(G) – матрица смежности псевдографа G=(V,X) (ориентированного или неориентированного).Обозначим через Ak=[a(k)ij] k-ю степень матрицы смежности A.
Элемент a(k)ij матрицы Ak ориентированного псевдографа (псевдографа) G равен числу всех путей (маршрутов) длины k из vi в vj.
Матрица достижимости ориентированного графа G − квадратная матрица T(G)=[tij] порядка n, элементы которой равны:
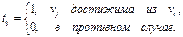
Матрица сильной связности ориентированного графа G − квадратная матрица S(G)=[sij] порядка n, элементы которой равны:
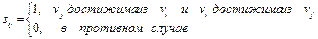
Матрица связности графа G − квадратная матрица S(G)=[sij] порядка n, элементы которой равны
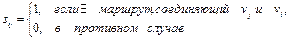
Деревья
Неориентированным деревом(или просто деревом) называется связный граф без циклов. Этому определению эквивалентны следующие определения:
а) дерево есть связный граф, содержащий n вершин и n - 1 ребер;
б) дерево есть граф, любые две вершины которого можно соединить простой цепью.
Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом.
Пример 4.9. Графы, изображенные на рис. 4.5, являются деревьями. Можно интерпретировать рис. 4.5 как лес, состоящий из трех деревьев.
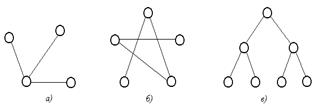
Рис. 4.5
Остовным деревомсвязного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.
Пример 4.10. Для графа, изображенного на рис. 4.6 а), графы на рис. 4.6 б) и 4.6 в) являются остовными деревьями.
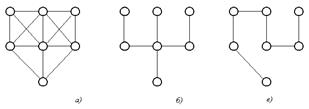
Рис. 4.6
Пусть граф G имеет n вершин и m ребер Так как всякое дерево с n вершинами по определению имеет n – 1 ребер, то любое остовное дерево графа G получается из этого графа в результате удаления m –(n – 1) = m – n + 1 ребер. Число g = m – n + 1 называется цикломатическим числомграфа.
Примеры тестовых заданий
ЗАДАНИЕ N 4.1 ( - выберите один вариант ответа)
Реализацией графа с множеством вершин V={1,2,3,4} и списком дуг Е={(1;4),(1;3),(2;2),(2;4),(3;1)} является…
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 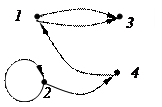 | 2) | 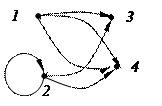 | |
| 3) | 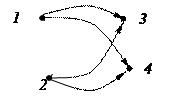 | 4) | 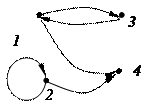 |
Решение. По условию из 1-й вершины выходит две дуги: (1;4) и (1;3), поэтому 1-й и 2-й варианты неверны. Петля, соответствующая дуге (2, 2) отсутствует в 3-ем варианте, она есть в 4-м варианте. Сопоставив список дуг с рисунком для 4-го варианта, получим, что верный ответ 4).
ЗАДАНИЕ N 4.2 (- выберите один вариант ответа)
Матрица  является матрицей смежности ориентированного графа. Тогда списком ребер ориентированного графа является …
является матрицей смежности ориентированного графа. Тогда списком ребер ориентированного графа является …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 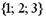 | 2) | 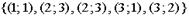 | |
| 3) | 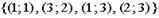 | 4) | 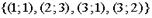 |
Решение. Поскольку в матрице смежности а11=а31=а32=1, то граф содержит дуги (ориентированные ребра) (1,1), (3,1), (3,2), а поскольку а23 =2, то дуга (2, 3) имеет кратность 2. Верный ответ: 2).
ЗАДАНИЕ N 4.3 ( - выберите один вариант ответа)
Матрица смежности ориентированного графа
равна …
ВАРИАНТЫ ОТВЕТОВ:
| 1) |  | 2) |  | 3) |  | 4) |  |
Решение. Из рисунка видно, что дугами графа являются (1, 2), (1, 3), (2 ,3), (3, 4), (4, 1), поэтому соответствующие элементы матрицы смежности а12, а13, а23, а34, а41 равны единице, остальные элементы равны нулю. Верный ответ: 4).
ЗАДАНИЕ N 4.4 (  - выберите варианты согласно тексту задания)
- выберите варианты согласно тексту задания)
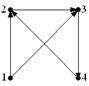
Неориентированные графы имеют множество вершин 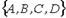 . Множества их ребер заданы отношением инцидентности: каждое ребро представлено как пара вершин. Поставьте в соответствие каждому графу его графическое изображение.
. Множества их ребер заданы отношением инцидентности: каждое ребро представлено как пара вершин. Поставьте в соответствие каждому графу его графическое изображение.
1. 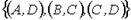
2. 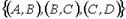
3. 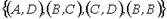
ВАРИАНТЫ ОТВЕТОВ:
A) 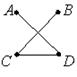 B)
B) 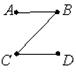 C)
C) 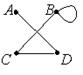 D)
D) 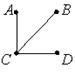 E)
E) 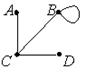
Решение. 1-й и 2-й списки содержат по три дуги, из рисунков A), B), D) дуга (A,D) имеется лишь у графа А), дуга (А,В) – у графа В). Третий список содержит четыре дуги, как и на рис. С), Е), причем дуга (A,D) есть лишь у графа С). Сопоставив остальные дуги графов, убеждаемся, что веерный ответ: 1 – А); 2 – В); 3 – С).
 |
ЗАДАНИЕ N 4.5 ( - выберите один вариант ответа)
Для ориентированного графа, изображенного на рисунке
полный путь может иметь вид …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 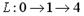 | 2) | 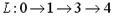 | |
| 3) | 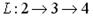 | 4) | 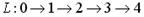 |
Решение. Обычно в теории графов под полным путем понимается Гамильтонов путь, т.е. проходящий через все вершины графа. Для заданного графа такого пути не существует. Из предложенных вариантов 4-й путь содержит все вершины, но дуги (1, 2) нет в графе. Поскольку в графе есть исток: вершина 1 не имеет входящих дуг, и сток: вершина 4 не имеет исходящих дуг, то здесь под полным путем понимается путь, из истока (вершины 1) в сток (вершину 4), т.е путь 0 ® 1 ® 4. Верный ответ: 1.
ЗАДАНИЕ N 4.6 ( - выберите один вариант ответа)
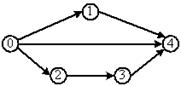
Число полных путей в ориентированном графе, представленном матрицей смежности
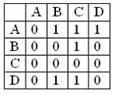
равно …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 2) | 3) | 4) |
 Решение. По заданной матрице смежности построим граф. Из рис. видно, что вершина А является истоком, т.к. не имеет входящих дуг (столбец А в матрице смежности не содержит 1); вершина С является стоком, т.к. не имеет исходящих дуг (строка С в матрице смежности не содержит 1). Полные пути – это пути из вершины А в вершину С, т.е. А®С; A®D®C; A®B®C; A®D®B®C. Т.о. число полных путей 4. Верный ответ: 4).
Решение. По заданной матрице смежности построим граф. Из рис. видно, что вершина А является истоком, т.к. не имеет входящих дуг (столбец А в матрице смежности не содержит 1); вершина С является стоком, т.к. не имеет исходящих дуг (строка С в матрице смежности не содержит 1). Полные пути – это пути из вершины А в вершину С, т.е. А®С; A®D®C; A®B®C; A®D®B®C. Т.о. число полных путей 4. Верный ответ: 4).
