Основные тождества алгебры множеств
Для любых множеств A, B, C справедливы следующие тождества:
1. Коммутативность.
а) A È B = B È A (для объединения); б) A Ç B = B Ç A (для пересечения).
2. Ассоциативность.
а) A È (B È C) = (A È C) È C (для объединения);
б) A Ç (B Ç C) = (A Ç B) Ç C (для пересечения).
3. Дистрибутивность.
а) AÈ (BÇC) = (AÈB)Ç(AÈC) (для объединения относительно пересечения);
б) AÇ(BÈC) = (AÇB)È(AÇC) (для пересечения относительно объединения).
4. Закон де Моргана.
а) 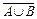 =
= 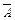 Ç
Ç 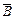 (дополнение к объединению есть пересечение дополнений);
(дополнение к объединению есть пересечение дополнений);
б) 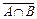 =
= 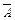 È
È 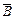 (дополнение к пересечению есть объединение дополнений).
(дополнение к пересечению есть объединение дополнений).
5. Идемпотентность.
а) A È A = A (для объединения);
б) A Ç A = A (для пересечения).
6. Поглощение.
а) A È (A Ç B) = A;
б) A Ç (A È B) = A.
7. Расщепление (склеивание).
а) (A È B) Ç (A È 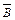 ) = A;
) = A;
б) (A Ç B) È (A Ç 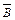 ) = A.
) = A.
8. Двойное дополнение. 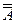 = A.
= A.
9. Закон исключенного третьего.  A È
A È 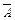 = U.
= U. 
10. Операции с пустым и универсальным множествами.
| а) A È U = U; | г) A Ç Æ = Æ; |
| б) A È Æ = A; | д) 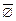 = U; = U; |
в) A Ç U = A;  | е) 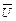 = Æ = Æ |
11. А \ В = A Ç 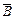 .
.
Основные тождества алгебры множеств можно использовать для доказательства других тождеств.
Пример 1.22. Доказать тождество (AÈB) \ В = A Ç 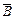 .
.
Преобразуем левую часть тождества, используя тождество 11:
(AÈB) \ В = (AÈB) Ç 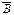 .
.
Затем используем закон дистрибутивности (тождество 3б):
(AÈB) Ç 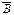 = A Ç
= A Ç 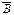 ÈB Ç
ÈB Ç 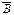 .
.
Используем закон исключенного третьего (тождество 9): B Ç 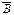 = Æ.
= Æ.
Получим: A Ç 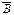 ÈB Ç
ÈB Ç 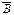 = A Ç
= A Ç 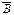 È Æ.
È Æ.
Используем свойство пустого множества (тождество 10б): A Ç 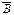 È Æ = A Ç
È Æ = A Ç 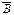 .
.
Тождество доказано.
Доказательство тождеств можно проиллюстрировать с помощью диаграмм Венна.
Пример 1.23. Доказать тождество: A \ (В \ C) = (A \ В)È (A Ç C).
Множества, стоящие в левой и правой частях тождества, изобразим с помощью диаграмм Эйлера – Венна (рис. 1.3).
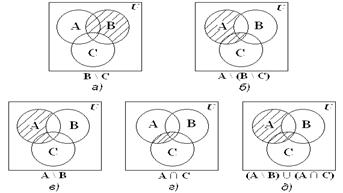
Рис. 1.3
Рис. 1.3б) и рис. 1.3д) иллюстрируют равенство множеств A \ (В \ C) и (A \ В)È(A ÇC).
Примеры тестовых заданий
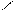
 ЗАДАНИЕ N 1.1 ( - выберите один вариант ответа)
ЗАДАНИЕ N 1.1 ( - выберите один вариант ответа)
Операцией над множествами А и В, результат которой выделен на рисунке,
 |
является…
ВАРИАНТЫ ОТВЕТОВ:
| 1) |  | 2) |  | |
| 3) | 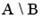 | 4) | 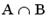 |
Решение следует из определения пересечения множеств и рис. 1.1 в) Верный ответ: 4) 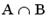
ЗАДАНИЕ N 1.2 ( - выберите один вариант ответа)
Число 2,5 принадлежит множеству…
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 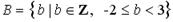 | 2) | 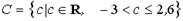 | |
| 3) | 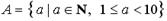 | 4) | 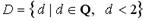 |
Решение. 2,5ÏZ, 2,5ÏN; 2,5ÎQ, но 2,5>2, поэтому 2,5ÏD. 2,5ÎR, неравенство
-3<2,5<2,6 выполняется, поэтому 2,5ÎС. Верный ответ: 2)
ЗАДАНИЕ N 1.3 ( - выберите один вариант ответа)
А и В – множества действительных чисел: 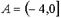 ,
, 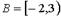 .
.
Тогда множество 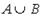 равно
равно
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 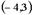 | 2) | 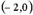 | 3) | 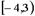 | 4) | 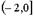 |
Решение. Изобразим множества А и В на числовой прямой:









Рис. 1.3
Из определения объединения множеств 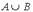 , рис. 1.1 б) и рис. 1.3 следует, что
, рис. 1.1 б) и рис. 1.3 следует, что 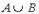 = (-4; 3). Верный ответ 1).
= (-4; 3). Верный ответ 1).
ЗАДАНИЕ N 1.4 ( - выберите один вариант ответа)
Даны множества A={b,y} и B={1,2,3}. Тогда декартовым (прямым) произведением 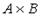 является …
является …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | {(b,y,1),(b,y,2),(b,y,3)} | 2) | {b,y,1,2,3} | |
| 3) | {(1,b),(1,y),(2,b),(2,y),(3,b),(3,y)} | 4) | {(b,1),(b,2),(b,3),(y,1),(y,2),(y,3)} |
Решение. Из определения декартова произведения двух множеств следует, что оно содержит упорядоченные пары из двух элементов (варианты ответов 1, 2 – неверны), порядок следования элементов тот же, что у множеств в произведении, поэтому верный ответ 4).
ЗАДАНИЕ N 1.5 ( - выберите несколько вариантов ответа)
Элементами множества натуральных чисел являются …
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 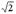 | 2) | 3) | - 5 | 4) | 5) |
Решение. Натуральные числа это целые положительные числа, т.е. 3 и 101. Верный ответ: 4), 5).
ЗАДАНИЕ N 1.6 ( - выберите несколько вариантов ответа)
Даны два множества 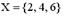 ,
, 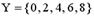 . Из предложенных высказываний верными являются…
. Из предложенных высказываний верными являются…
ВАРИАНТЫ ОТВЕТОВ:
| 1) | 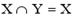 | 2) | 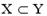 | 3) | 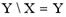 | 4) | 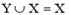 |
Решение. Очевидно, что XÌY; XÇY={2,4,6}=X; Y\X={0, 8}¹Y; YÈX={0,2,4,6,8}=Y¹X. Верный ответ: 1), 2).
Отображения. Отношения
Отображение множеств
Если каждому элементу хÎХ поставлен в соответствие один и только один элемент yÎY, то говорят, что определено отображение f множества X во множество Y. Обозначают y=f(x). Элемент у есть образ элемента х при данном отображении f, х - прообраз элемента у.
Отображение f -1, при котором каждому элементу множества Y ставится его прообраз из множества Х, называется обратным отображением для f.
Частным случаем отображения множества X во множество Y является отображение множества X на множество Y.
Отображение f множества X в Y называется сюръективным (отображением множества X на Y), если каждый элемент yÎY имеет хотя бы один прообраз.
Отображение X в Y называется инъективным, если для каждого элемента yÎY существует не более одного прообраза.
Если отображение f сюръективно и инъективно, оно называется биективным (взаимно-однозначным).
Пример 2.1. Пусть Х={а, b, с, d}, Y={2, 4, 6}, Z={m, n, k, q}. Зададим отображения
f1: Х ® Y; f2: Х ® Y; f3: Y ® Z; f4: X ® Z:
| f1: | a ® 2 | f2: | a ® 6 | f3: | 2 ® n | f4: | a ® m |
| b ® 4 | b ® 4 | 4 ® q | b ® q | ||||
| c ® 4 | c ® 4 | 6 ® k | c ® k | ||||
| d ® 6 | d ® 6 | d ® n |
Отображение f1 X в Y является сюръективным, но не является инъективным (элемент "4" имеет два прообраза). Отображение f2 несюръективно (элемент "2" не имеет прообраза) и неинъективно. Отображение f3 является инъективным, но несюръективно (элемент " m" не имеет прообраза) и неинъективно. Отображение f4 сюръективно и инъективно, т.е. является биективным.
Обратными для рассматриваемых отображений являются:
| f1-1 : | 2® a | f2-1: | 2 ® Æ | f3-1: | m ® Æ | f4-1: | m ® a |
| 4 ® {b, c} | 4 ®{b, c} | n ® 2 | n ® d | ||||
| 6® d | 6® {a, d} | k ® 6 | k ® c | ||||
| q ® 4 | q ® b |
Очевидно, биективное отображение между конечными множествами X и Y возможно только в случае, когда число элементов этих множеств совпадает.
Пример 2.2. Биективным отображением для бесконечных множеств может является, например, отображение f, установленное между множеством натурального ряда чисел А={1, 2, 3, ... n, ...} и множеством четных положительных чисел В={2, 4, 6,...} по типу n « 2n.
Пусть f : X ®Y и g : Y ®Z - некоторые отображения. Суперпозицией этихотображений называется отображение f g : X ®Z, определяемое следующим образом: (f g)(x)=g(f(x)), xÎ X .
Заметим, что суперпозиция определена не для любых пар отображений. Однако суперпозиция двух преобразований одного и того же множества определена всегда.
