Элементы дискретной математики

Е.И. Балабан

Элементы дискретной математики

Учебное пособие

г. Коломна

Введение

Дискретная математика является одним из разделов математики, изучаемым студентами специальностей 220201 – Управление и информатика в технических системах, 230105 – Программное обеспечение вычислительной техники и автоматизированных систем, 140501 - Двигатели внутреннего сгорания и 270102 – Промышленное и гражданское строительство.

Учебное пособие содержит основные определения по теории множеств, комбинаторике, теории графов и математической логике. Приведены многочисленные примеры и иллюстрации, рассмотрены тестовые задачи, предлагавшиеся при проведении Интернет-экзамена в 2006-2008 гг.

Данное учебное пособие может быть использовано как при изучении курса «Дискретная математика», так и для подготовке студентов к Интернет-экзамену. Оно содержит лишь основные понятия дискретной математики, поэтому для более глубокого изучения теоретического материала, а также методов и примеров решения задач решения, требует от студентов обращения к фундаментальным учебным пособиям [1 - 7] и конспекту лекций.

Элементы теории множеств

Множества и его элементы

Понятие множества является аксиоматичным и поэтому формально не может быть определено. Под множеством понимается совокупность каких-либо объектов, обладающим общим для всех характеристическим свойством.

Пример 1.1. Следующие совокупности объектов являются множествами: множество деревьев в лесу, множество целых чисел, множество корней уравнения
sin x = 0,5.

Всякое множество состоит из элементов. Множества обозначают прописными буквами, например А. В, С, а элементы – строчными буквами, например, а, b, c.

Если элемент a принадлежит множеству А, это записывается следующим образом: a Î А. Если элемент a непринадлежит множеству А, то записывают так: a Ï А.

Пример 1.2. Пусть А₁ – множество простых чисел, А₂ – множество целых чисел,
a = 4. Тогда a Î А₂, a Ï А₁.

Множество можно задать перечислением принадлежащих ему элементов или указанием свойств, которым элементы множества должны удовлетворять. Используются следующие обозначения: А = {a₁, a₂, a₃} – множество, состоящее из трех элементов; А = {a₁, a₂, …} – множество, состоящее из бесконечного числа элементов; {хÎА | Р(х)} – множество, состоящее из элементов множества А, обладающих свойством Р, а если из контекста ясно, о каком множестве А идет речь, то {х | Р(х)}.

Множество может состоять из элементов, которые сами являются множествами. Нужно различать элемент a и множество, состоящее из единственного элемента a.

Пример 1.3. Множество А = {1, 2} состоит из двух элементов 1, 2; но множество {А} состоит из одного элемента А.

Принято обозначать: N={1, 2, 3, 4,…} – множество натуральных чисел;
Z={…, -3, -2, -1, 0, 1,2,3,…} – множество целых чисел; Q= 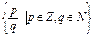- множество рациональных чисел; R – множество действительных (вещественных) чисел, С – множество комплексных чисел.

Если каждый элемент множества А является элементом множества В, говорят, что множество А является подмножеством множества В,и записывают
А Í В или В Ê А. Отметим, что по определению само множество А является своим подмножеством, т.е. А Í А. Если А Í В и А ¹ В, то А есть собственное подмножество В, А Ì В.

Пример 1.4. Пусть А – множество четных чисел, В – множество целых чисел, С –множество нечетных чисел. Тогда А Ì В, С Ì В, А Ë С, В Ë А.

Пример 1.5. Справедливы следующие включения: NÌ Z; Z ÌQ; Q ÌR; RÌ С.

Множества А и В называются равными или совпадающими (обозначается А= В), если они состоят из одних и тех же элементов, т.е. если АÍВ: и В ÍА.

Не надо смешивать отношение принадлежности (Î) и отношение включения (Í).

Пример 1.6. Пусть А = {2} – множество, состоящее из одного элемента,
В = {{2}, {4}} – множество, состоящее из двух элементов, каждое из которых является одноэлементным множеством. Тогда имеют место следующие соотношения: 2 Î {2}; {2} Ì {{2}, {4}}; 2 Ï {{2}, {4}}.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Æ. Принято считать, что пустое множество является подмножеством любого множества, Æ Í А, где А – любое множество. Таким образом, всякое множество содержит в качестве своих подмножеств пустое множество и само себя.

Пример 1.7. Множество корней уравнения sinx = 2 является пустым.

Множество всех подмножеств данного множества А называется множеством-степенью (семейством множеств А или булеаном) и обозначается P(A) (b(А) или 2^А). Если множество А состоит из n элементов, то P (A) состоит из 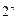элементов.

Существуют следующие способы задания множеств.

1. Перечислением элементов множества.

Пример 1.8. A = {1, 3, 5, 7, 9} – конечное множество; B = {1, 2, …, n, …} – бесконечное множество; D={Æ, {a}, {b}, {a, b}} – булеан множества F={a, b}.

2. Указанием свойств элементов множества. Для этого способа пользуются следующим форматом записи: A = {a çуказание свойства элементов}. Здесь a является элементом множества A, a Î А.

Пример 1.9. A = {a ça – простое число} – множество простых чисел;

B = {b çb² – 1 = 0, b Î R} – множество, состоящее из двух элементов, B = {– 1, 1};

D = 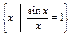– множество, состоящее из одного числа, x = 0.

3. С помощью порождающей процедуры, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть построены с помощью такой процедуры.

Пример 1.10. 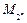- множество всех целых чисел, являющихся степенями двойки может быть задано двумя правилами, называемыми рекурсивными или индуктивными: а) 1Î 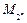; б) если m Î 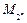, то 2m Î .

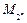Для удобства и краткости записей в дальнейшем будем пользоваться специальными обозначениями – кванторами: слова «любой», «каждый» будем обозначать с помощью квантора " (общности), слова «существует», «найдется» - с помощью квантора $ (существования).

Операции над множествами

Рассмотрим основные операции над множествами.

Объединением множеств А и В называется множество АÈВ, все элементы которого являются элементами хотя бы одного из множеств А или В:

АÈВ = {x ç xÎ А или xÎВ}.

Аналогично определяется объединение нескольких множеств А_i, где индексы i пробегают множество I: 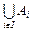={x| $ iÎI: xÎ А_i}.

Пример 1.11. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда АÈВ = {2, 4, 5, 6}.

Пересечением множеств А и В называется множество АÇВ, все элементы которого являются элементами обоих множеств А и В: АÇВ = {x çxÎ А и xÎВ}.

Аналогично определяется пересечение нескольких множеств.

Пример 1.12. Пусть А = {4, 5, 6}, В = {2, 4, 6}. Тогда АÇВ = {4, 6}.

Если множества не имеют ни одного общего элемента, то говорят, что множества не пересекаются или что их пересечение – пустое множество.

Пример 1.13. Пусть А = {1, 2}, В = {2, 3}, C = {3, 4}. Тогда АÇВÇC =Æ.

Разностью множеств В и А (относительным дополнением множества В до множества А) называется множество А \ В, все элементы которого являются элементами множества А, но не являются элементами множества В:

А \ В = {x ç xÎ А и xÏВ}.

Пример 1.14. А = {4, 5, 6}, В = {2, 4, 6}. А \ В = {4, 5}, В \ А= {2}.

Симметрической разностью множеств А и В называется множество
А Å В=А D В=: (А \ В) È (В \ А).

Пример 1.15. А={3,4, 5, 6}, В ={2, 4, 6}. А \ В = {3, 5}, В \ А= {2}, АÅВ = {2, 3, 5}.

Универсальным множеством называется такое множество U, что все рассматриваемые в данной задаче множества являются его подмножествами.

Дополнением множества А называется множество 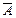всех таких элементов x Î U, которые не принадлежат множеству А: 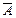= U \ A.

Пример 1.16. Пусть U – множество всех натуральных чисел, а А – множество положительных четных чисел, тогда 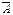– множество положительных нечетных
чисел.

Для наглядного представления множеств и отношений между ними используется диаграммы Венна (иногда их называют кругами Эйлера или диаграммами Эйлера – Венна).

Универсальное множество U изображают в виде прямоугольника, а множества, входящие в универсальное множество, – в виде кругов внутри прямоугольника; элементу множества соответствует точка внутри круга (рис 1.1 а).

С помощью диаграмм Венна удобно иллюстрировать операции над множествами: объединения (рис 1.1 б), пересечения (рис 1.1 в), разности (рис 1.1 г), симметричной разности (рис 1.1 д), дополнения (рис 1.1 е).

АÅВ

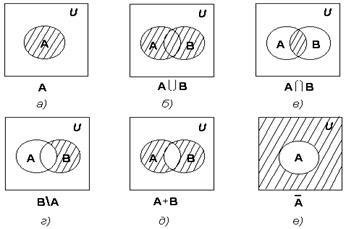
Рис.1.1

Алгебра множеств

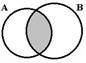
Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, 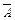Ç (ВÈC), (А \ В) + C – формулы алгебры множеств.

Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если xÎ А, то xÎВ и, во-вторых, если xÎВ, то xÎ А.

Пример 1.21. Докажем таким образом, например, свойство дистрибутивности для объединения (тождество 3а)): AÈ (BÇC) = (AÈB) Ç (AÈC).

1. Сначала предположим, что некоторый элемент x принадлежит левой части тождества, т.е. xÎ AÈ (BÇC), и докажем, что x принадлежит правой части, т.е. xÎ(AÈB) Ç (AÈC).

Действительно, пусть xÎ AÈ (BÇC). Тогда либо xÎ A, либо xÎ BÇC. Рассмотрим каждую из этих возможностей.

Пусть xÎ A. Тогда xÎ A È B и xÎ A ÈC (это верно для любых множеств B и C). Следовательно, xÎ(AÈB) Ç (AÈC).

2. Предположим, что некоторый элемент x принадлежит правой части тождества, т.е. xÎ (AÈB) Ç (AÈC), и докажем, что x принадлежит левой части, т.е. xÎ AÈ (BÇC) .

Действительно, пусть xÎ (AÈB) Ç (AÈC). Тогда xÎAÈB, и одновременно xÎ AÈC. Если xÎ AÈB, то либо xÎ A, либо xÎ B, если .xÎ AÈC, то либо xÎ A, либо xÎ C. Пусть xÎ A, Тогда xÎ AÈ (BÇC) и утверждение доказано. Если xÏ A, то одновременно должны выполняться условия xÎ B и xÎ C, т.е. xÎ BÇC. Но тогда xÎ BÇC и xÎ AÈ (BÇC), что также доказывает наше утверждение.

Примеры тестовых заданий

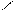
ЗАДАНИЕ N 1.1 ( - выберите один вариант ответа)
Операцией над множествами А и В, результат которой выделен на рисунке,

является…

ВАРИАНТЫ ОТВЕТОВ:

1)			2)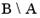
3)		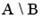	4)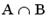

Решение следует из определения пересечения множеств и рис. 1.1 в) Верный ответ: 4)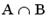

ЗАДАНИЕ N 1.2 ( - выберите один вариант ответа)
Число 2,5 принадлежит множеству…

ВАРИАНТЫ ОТВЕТОВ:

1)		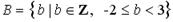	2)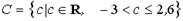
3)		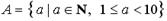	4)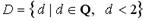

Решение. 2,5ÏZ, 2,5ÏN; 2,5ÎQ, но 2,5>2, поэтому 2,5ÏD. 2,5ÎR, неравенство
-3<2,5<2,6 выполняется, поэтому 2,5ÎС. Верный ответ: 2)

ЗАДАНИЕ N 1.3 ( - выберите один вариант ответа)
А и В – множества действительных чисел: , .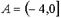
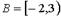Тогда множеств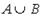о равно

ВАРИАНТЫ ОТВЕТОВ:

1)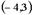

2)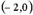

3)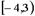

4)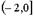

Решение. Изобразим множества А и В на числовой прямой:

Рис. 1.3

Из определения объединения множеств 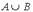, рис. 1.1 б) и рис. 1.3 следует, что 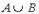= (-4; 3). Верный ответ 1).

ЗАДАНИЕ N 1.4 ( - выберите один вариант ответа)
Даны множества A={b,y} и B={1,2,3}. Тогда декартовым (прямым) произведением 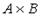является …

ВАРИАНТЫ ОТВЕТОВ:

1)	{(b,y,1),(b,y,2),(b,y,3)}		2)	{b,y,1,2,3}
3)	{(1,b),(1,y),(2,b),(2,y),(3,b),(3,y)}		4)	{(b,1),(b,2),(b,3),(y,1),(y,2),(y,3)}

Решение. Из определения декартова произведения двух множеств следует, что оно содержит упорядоченные пары из двух элементов (варианты ответов 1, 2 – неверны), порядок следования элементов тот же, что у множеств в произведении, поэтому верный ответ 4).

ЗАДАНИЕ N 1.5 ( - выберите несколько вариантов ответа)
Элементами множества натуральных чисел являются …

ВАРИАНТЫ ОТВЕТОВ:

1)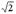

2)

3)

- 5

4)

5)

Решение. Натуральные числа это целые положительные числа, т.е. 3 и 101. Верный ответ: 4), 5).

ЗАДАНИЕ N 1.6 ( - выберите несколько вариантов ответа)
Даны два множества 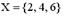, 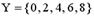. Из предложенных высказываний верными являются…

ВАРИАНТЫ ОТВЕТОВ:

1)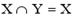

2)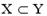

3)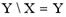

4)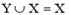

Решение. Очевидно, что XÌY; XÇY={2,4,6}=X; Y\X={0, 8}¹Y; YÈX={0,2,4,6,8}=Y¹X. Верный ответ: 1), 2).

Отображения. Отношения

Отображение множеств

Если каждому элементу хÎХ поставлен в соответствие один и только один элемент yÎY, то говорят, что определено отображение f множества X во множество Y. Обозначают y=f(x). Элемент у есть образ элемента х при данном отображении f, х - прообраз элемента у.

Отображение f ^-1, при котором каждому элементу множества Y ставится его прообраз из множества Х, называется обратным отображением для f.

Частным случаем отображения множества X во множество Y является отображение множества X на множество Y.

Отображение f множества X в Y называется сюръективным (отображением множества X на Y), если каждый элемент yÎY имеет хотя бы один прообраз.

Отображение X в Y называется инъективным, если для каждого элемента yÎY существует не более одного прообраза.

Если отображение f сюръективно и инъективно, оно называется биективным (взаимно-однозначным).

Пример 2.1. Пусть Х={а, b, с, d}, Y={2, 4, 6}, Z={m, n, k, q}. Зададим отображения
f₁: Х ® Y; f₂: Х ® Y; f₃: Y ® Z; f₄: X ® Z:

f1:	a ® 2	f2:	a ® 6	f3:	2 ® n	f4:	a ® m
	b ® 4		b ® 4		4 ® q		b ® q
	c ® 4		c ® 4		6 ® k		c ® k
	d ® 6		d ® 6				d ® n

Отображение f₁ X в Y является сюръективным, но не является инъективным (элемент "4" имеет два прообраза). Отображение f₂ несюръективно (элемент "2" не имеет прообраза) и неинъективно. Отображение f₃ является инъективным, но несюръективно (элемент " m" не имеет прообраза) и неинъективно. Отображение f₄ сюръективно и инъективно, т.е. является биективным.

Обратными для рассматриваемых отображений являются:

f1-1 :	2® a	f2-1:	2 ® Æ	f3-1:	m ® Æ	f4-1:	m ® a
	4 ® {b, c}		4 ®{b, c}		n ® 2		n ® d
	6® d		6® {a, d}		k ® 6		k ® c
					q ® 4		q ® b

Очевидно, биективное отображение между конечными множествами X и Y возможно только в случае, когда число элементов этих множеств совпадает.

Пример 2.2. Биективным отображением для бесконечных множеств может является, например, отображение f, установленное между множеством натурального ряда чисел А={1, 2, 3, ... n, ...} и множеством четных положительных чисел В={2, 4, 6,...} по типу n « 2n.

Пусть f : X ®Y и g : Y ®Z - некоторые отображения. Суперпозицией этихотображений называется отображение f g : X ®Z, определяемое следующим образом: (f g)(x)=g(f(x)), xÎ X .

Заметим, что суперпозиция определена не для любых пар отображений. Однако суперпозиция двух преобразований одного и того же множества определена всегда.

Бинарные отношения

Для непустых множеств X, Yбинарным (или двуместным)отношением S называется множество упорядоченных пар <x, y>ÎS ÍX´Y.

Если пара <x, y> принадлежит S, то это записывается следующим образом: <x, y> Î S или, что то же самое, x S y.

Пример 2.7. S = {<1, 1>, <1, 2>, <2, 3>} или 1 S 1 , 1 S 2, 2 S 3.

Аналогично можно определить n-местное отношение как множество упорядоченных n-ок.

Так как бинарное отношение – множество, то способы задания бинарного отношения такие же, как и способы задания множества (см. разд. 1.1). Бинарное отношение может быть задано перечислением упорядоченных пар или указанием общего свойства упорядоченных пар.

Пример 2.8. S₁ = {<1, 2>, <2, 1>, <2, 3>} – отношение задано перечислением упорядоченных пар; S₂ = {<x, y> çx+ y = 7, x, y – действительные числа} – отношение задано указанием свойства x+ y = 7.

Областью определения бинарного отношения S называется множество

D_S = {x ç$ y: x S y}.

Свойства отношений

Среди бинарных отношений на множествах выделяются некоторые, обладающие общими свойствами.

Отношение S называется рефлексивным на множестве X, если для любого xÎ X выполняется x S x, т.е. ("x),(x, x)Î S.

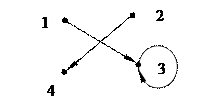а) Граф отношения из примера 2.9	b) Граф отношения из примера 2.10
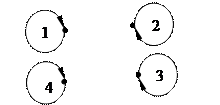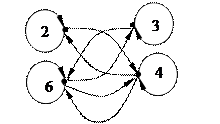с) Граф отношения «быть равными» на множестве {1, 2, 3 ,4}	d) Граф отношения «иметь общий делитель» на множестве {2, 3 ,4, 6}

Рис. 2.1. Графы бинарных отношений

В матрицах рефлексивных отношений на главной диагонали стоят единицы. У графа такого отношения все вершины имеют петли.

Пример 2.13. Рефлексивными являются отношения «быть равными» (рис. 2.1 с), «быть не меньше», «иметь общий делитель» (рис. 2.1 d) на множестве чисел; «быть подмножеством» на множестве множеств, «жить в одном городе» на множестве людей.

Отношение S называется нерефлексивным на множестве X, если ($x),
(x, x)Ï S и антирефлексивным если. ("x),(x, x)Ï S.

Отношение S называется симметричным на множестве X, если для любых x, y Î X из xSy следует yS x.

Матрицы симметричных отношений симметричны (равны транспонированным). У графа такого отношения все дуги имеют встречные.

Пример 2.14. Симметричными являются отношения «быть равными» (рис. 2.1 с), «быть не меньше», «иметь общий делитель» (рис. 2.1 d) на множестве чисел; «быть подмножеством» на множестве множеств, «жить в одном городе» на множестве людей.

Отношение S называется антисимметричным на множестве X, если для любых x, y Î X из x S y и y S x следует x = y.

Отношение S называется асимметричным на множестве X, если ни для одной пары x, y Î X не выполняется одновременно x S y и y S x.

Пример 2.15. а) Пусть X – конечное множество, X = {1, 2, 3} и r = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>, <3, 3>}. Отношение S антисимметрично.

б) Отношение G = {<1, 1>, <1, 2>, <1, 3>, <2, 1>, <2, 3>, <3, 3>} не антисимметрично. Например, <1, 2> ÎG, и <2, 1> ÎG, но 1 ¹2.

в) На множество действительных чисел отношение £ (меньше или равно) антисимметрично.

г) На множество действительных чисел отношение > (больше) асимметрично.

Отношение S называется транзитивным на множестве X, если для любых
x, y, z Î X из xSy и yS z следует xSz.

Одновременное выполнение условий xSy, yS z, xS z означает, что пара
<x, z> принадлежит композиции S 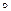S. Поэтому для транзитивности S необходимо и достаточно, чтобы множество S 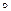S являлось подмножеством S, т. е. S 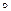S Í S.

Пример 2.16. а) Пусть X – конечное множество, X= {1, 2, 3} и S = {<1,1>,
<1 2>,<2,3>, <1, 3>}. Отношение S транзитивно, т. к. наряду с парами <x, y>и <y, z>имеется пара<x, z>. Например, наряду с парами <1,2>, и <2,3> имеется пара <1,3>.

б) На множестве действительных чисел отношение £ (меньше или равно) транзитивно, т.к. если x£ y и y£ z , то x£ z.

в) Пусть X – множество людей, отношение "быть старше" транзитивно, т.к. если x старше y и y старше z , то x старше z.

Отношение S называется отношением эквивалентности на множестве X, если оно рефлексивно, симметрично и транзитивно на множестве X.

Пример 2.17. Отношениями эквивалентности являются отношение равенства на множестве чисел, отношение "учиться в одной группе" на множестве студентов.

Пусть S – отношение эквивалентности на множестве X и xÎ X. Классом эквивалентности, порожденным элементом x, называется подмножество множества X, состоящее из тех элементов y Î X, для которых xSy. Класс эквивалентности, порожденный элементом x, обозначается через [x].

Классы эквивалентности образуют разбиение множества X, т. е. систему непустых попарно непересекающихся его подмножеств, объединение которых совпадает со всем множеством X.

Пример 2.18. а) Отношение равенства на множестве целых чисел порождает следующие классы эквивалентности: для любого элемента x из этого множества [x] = {x}, т.е. каждый класс эквивалентности состоит из одного элемента.

б) Класс эквивалентности, порожденный парой <x, y> определяется соотношением: [<x, y>] = 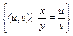. Каждый класс эквивалентности, порожденный парой <x, y>, определяет одно рациональное число.

в) Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы.

Отношение S называется отношением толерантности на множестве X, если оно рефлексивно, симметрично на множестве X.

Отношение S называется отношением частичного порядка (или просто частичным порядком) на множестве X, если оно рефлексивно, антисимметрично и транзитивно на множестве X. Множество X в этом случае называют частично упорядоченным и указанное отношение принято обозначать символом 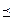, а, если это не приводит к недоразумениям, то £.

Пример 2.19. а) Пусть X = {1, 2, 3} и S = {<1, 1>, <1, 2>, <1, 3>, <2, 2>, <2, 3>,
<3, 3>}. Отношение S есть отношение частичного порядка.

б) Отношение А Í В на множестве подмножеств некоторого множества U есть отношение частичного порядка.

d) Отношение делимости на множестве натуральных чисел есть отношение частичного порядка.

Примеры тестовых заданий

ЗАДАНИЕ N 2.1 ( - введите ответ)
Отображение f множества всех целых чисел в себя определяется формулой 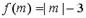. Тогда число элементов образа множества 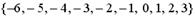при этом отображении равно …

ВАРИАНТЫ ОТВЕТОВ:

Решение. Найдем образы всех элементов исходного множества:

f(-6)=|-6|-3=3, f(-5)=|-5|-3=2, f(-4)=|-4|-3=1, f(-3)=|-3|-3=0, f(-2)=|-2|-3=-1,
f(-1)=|-1|-3= -2, f(0)=|0|-3= -3, f(1)=|1|-3= -2, f(2)=|2|-3= -1, f(0)=|3|-3= 0.

Т.о. образом заданного множества будет множество {-3, -2, -1, 0, 1, 2, 3}, которое состоит из семи элементов.

Заметим, что можно было учесть четность функции, задающей отображение, и из числа элементов исходного множества (10) вычесть число симметричных относительно нуля элементов в прообразе (-3 и 3б -2 и 2, -1 и 1): 10-3=7.

ЗАДАНИЕ N 2.2 ( - выберите один вариант ответа)
Образом отрезка 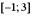при отображении 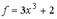является…

ВАРИАНТЫ ОТВЕТОВ:

1)	(– 1; 83)		2)	(5; 83)
3)	[– 1; 83]		4)	[9; 81]

Решение. Поскольку f`(x)=(3x<sup>3</sup>+2)`= 6x²≥0, то функция монотонна на области определения, в т.ч. на [-1; 3]. Из ее непрерывности вытекает, что образом отрезка является отрезок, конца которого являются образами концов заданного отрезка:
f`(-1)=3∙ (-1)<sup>3</sup>+2=-3+2= -1 ; f`(3)=3∙(3)³+2=81+2= 83. Образом отрезка [-1; 3] является отрезок [-1; 83]. Верный ответ 3).

ЗАДАНИЕ N 2.3 ( - выберите несколько вариантов ответа)
Бинарная алгебраическая операция 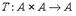на множестве 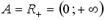не обладает свойством коммутативности, если …

ВАРИАНТЫ ОТВЕТОВ:

1)		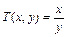	2)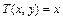
3)		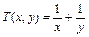	4)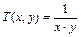

Решение. Коммутативность бинарной операции по определению состоит в выполнении равенства T(x,y)=T(y,x) для всех x, y из области определения. Проверим выполнение этого равенства для заданных операций:

; ; ; ;

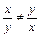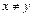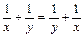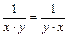Т.о. 1-я и 2-я из операция не обладает свойством коммутативности, а 3-я и4-я обладают. Верный ответ 1) 2).

ЗАДАНИЕ N 2.4 ( - выберите один вариант ответа)
Свойством транзитивности облает бинарное отношение…

ВАРИАНТЫ ОТВЕТОВ:

1)	«иметь разный рост»		2)	«быть перпендикулярными»
3)	«быть параллельными		4)	«быть отцом»

Решение. Проверим обладают ли свойством транзитивности заданные отношения.

1) Если А и В имеют разный рост (например, 179 и 175 см) и В и С имеют разный рост, то в случае, когда рост С 179 см, А и С имеют одинаковый рост. Т.о. отношение 1 нетранзитивно.

2) Рассмотрим прямые L₁, L₂ , L₃ на плоскости. Если L₁┴L₂, а L₂┴L₃, то L₁||L₃. Т.о. отношение 2 нетранзитивно.

3) Рассмотрим прямые L₁, L₂ , L₃ на плоскости или в пространстве. Если L₁ ||L₂, а
L₂ ||L₃, то L₁||L₃. Т.о. отношение 3 транзитивно.

4) Если А отец В, а В отец С, то А -дед С, но не отец. Т.о. отношение 4 нетранзитивно.

Верный ответ 3).

ЗАДАНИЕ N 2.5 ( - выберите один вариант ответа)
Бинарное отношение , обладает свойствами …

ВАРИАНТЫ ОТВЕТОВ:

1)	симметричности и транзитивности	2)	рефлексивности и транзитивности
3)	рефлексивности и симметричности	4)	антирефлексивности и симметричности

Решение. Проверим рефлексивность заданного отношения: 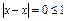, т.е. "хÎR xRx, отношение рефлексивно. Проверим симметричность: если 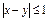, то поскольку 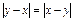получим: 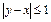, отношение симметрично. Проверим транзитивность: пусть х=4, у=3, z=2. Имеем: 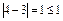, , 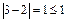, 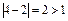т.е. для выбранных значений x, y, z отношение транзитивным не является, т.о. оно нетранзитивно. Верный ответ 3).

ЗАДАНИЕ N 2.6 ( - выберите несколько вариантов ответа)
Отношение «быть меньше» 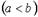на множестве действительных чисел является…

ВАРИАНТЫ ОТВЕТОВ:

1)	симметричным		2)	антирефлексивным
3)	рефлексивным		4)	транзитивным

Решение. Проверим рефлексивность заданного отношения: неравенство x<x неверно "хÎR, отношение антирефлексивно. Проверим симметричность: если x<y, то неравенство y<x неверно "х, yÎR, отношение несимметрично (асимметрично). Проверим транзитивность: пусть x<y, у<z, тогда очевидно, что x<z. Отношение транзитивно. Верный ответ 2) и 4).

Комбинаторика

Перестановки

Перестановками называют комбинации, состоящие из одних и тех же элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок из n элементов обозначается

P_n = n!=1×2×3×…×(n-1)×n

Пример 3.4. Сколькими способами шесть человек могут встать в очередь к кассе?

Решение. Так как каждому способу расстановки в очередь соответствует перестановка из восьми элементов, число способов будет перестановками без повторений. Следовательно: P₆ = 6!=1×2×3×4×5×6= 720.

Если некоторые из имеющихся n элементов повторяются, то в этом случае комбинации с повторениями называют перестановками с повторениями. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

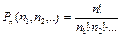, где n₁ + n₂ + … = n.

Пример 3.5. Требуется составить расписание отправления поездов на различные дни недели. При этом необходимо, чтобы: 3 дня отправлялись по 2 поезда в день, 2 дня – по 1 поезду в день, 2 дня – по 3 поезда в день. Сколько можно составить различных расписаний?

Решение. Количество поездов, отправляемых в день (числа 1,2,3), – это три группы одинаковых элементов, из которых должна быть составлена выборка. При этом в расписании на неделю число 1 повторяется 2 раза, число 2 повторяется 3 раза и число 3 повторяется 2 раза. Число различных расписаний равно

P₇(2,3,2)= 7!/(2!∙3!∙2!)=210.

Размещения

Размещением (без повторения) называются такие комбинации элементов, которые отличаются между собой или самими элементами или порядком их расположения в группе. Число всех размещений из n элементов по m обозначается 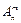и определяется по формуле: .

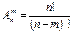Пример 3.6. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан выбор, если каждый член общества может занимать лишь один пост?

Решение. В данном случае надо найти число размещений (без повторений) из 25 элементов по 4. Ведь здесь играет роль и то, кто будет выбран в руководство общества, и то, какие посты займут выбранные. Поэтому ответ дается формулой

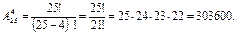
Размещением с повторениями называются такие комбинации элементов, которые отличаются между собой порядком их расположения в группе. Число всех размещен