Приведение сил инерции, приложенных к твердому телу, к простейшему виду

Главный вектор сил инерции равен производной по времени от количества движения 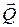с противоположным знаком:

,

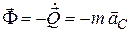где 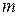- масса тела, 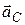- ускорение центра масс.

Главный момент сил инерции относительно неподвижного полюса :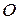

,

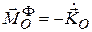где 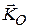- кинетический момент тела относительно полюса .

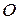(Кинетический момент относительно подвижного полюса определяется с помощью теоремы Кёнига).

Уравнения кинетостатики твердого тела

Для механической системы, состоящей из 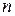материальных точек, можно составить 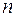уравнений кинетостатики в векторной форме:

, .

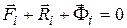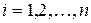Здесь 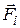- равнодействующая активных сил, приложенных к 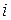- ой точке системы, 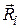- равнодействующая реакций связей, 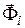- сила инерции. Совершая алгебраические действия над этими уравнениями, можно получить различные следствия из них, например:

а) главный вектор всех сил (задаваемых сил, реакций и сил инерции) равен нулю:

.

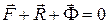б) главный момент всех сил относительно неподвижного полюса 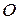равен нулю:

.

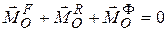Последние два уравнения являются уравнениями кинетостатики твердого тела. Записав их в проекциях на оси декартовой системы координат, получим 6 скалярных уравнений, что соответствует шести степеням свободы твердого тела в общем случае его движения.

3.3.3. Дифференциальные уравнения движения твердого тела можно вывести, например, из теорем об изменении количества движении (теорема о движении центра масс) и кинетического момента.

Поступательное движение тела описывается уравнениями

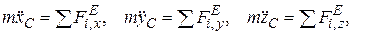
где 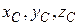- координаты центра масс, 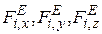- проекции внешних сил (задаваемых сил и реакций связей).

Вращение тела вокруг неподвижной оси описывается уравнением

,

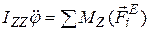где 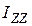- момент инерции тела относительно оси вращения ,

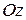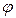- угол поворота тела, согласованный по направлению с осью ,

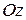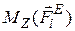- момент внешней силы относительно оси .

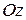Плоскопараллельное движение тела описывается уравнениями

, ,

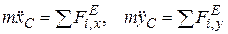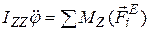где 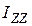- момент инерции тела относительно некоторой оси 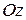, перпендикулярной плоскости движения.

Дифференциальные уравнения сферического движения содержат в своем выражении компоненты тензора инерции и проекции угловой скорости. Эти уравнения могут быть проинтегрированы в квадратурах только в специальных случаях.

Дифференциальные уравнения движения свободного твердого тела составляют обычно как уравнения движения центра масс и уравнения сферического движения вокруг центра масс.

Аналитическая механика

Классификация связей

Рассмотрим связи, заданные аналитически. Связи выражают условия, накладываемые на положения и скорости 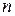точек, составляющих механическую систему.

А) Пусть условия связей (links) заданы как 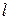неравенств:

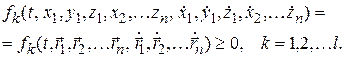
Связи в этом случае называются ограничивающими. Если условия связи заданы в виде равенств – уравнений связей

,

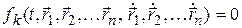то связи называются удерживающими (или напряженными).

Будем далее изучать механические системы, подчиненные удерживающим связям.

Б) Если уравнения связей явно содержат время, то связи называются нестационарными (или реономными – «текучими»). Иначе связи называются стационарными (или склерономными – «жесткими»).

В) Если уравнения связей содержат производные от координат, то связи называются дифференциальными, иначе они называются позиционными.

Если уравнения дифференциальных связей как дифференциальные уравнения относительно координат удается разрешить (проинтегрировать), то дифференциальные связи называются интегрируемыми. Механическая система, подчиненная позиционным или дифференциальным интегрируемым связям, называется голономной ( 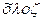– весь, целый; 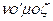– закон).

Г) Если реакции связей совершают нулевую работу при любых виртуальных перемещениях точек механической системы (см. ниже), то связи называются идеальными, иначе – неидеальными.

4.2. Виртуальные перемещения. Обобщенные силы

4.2.1. Виртуальные перемещения - это бесконечно малые перемещения 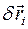точек механической системы, совместимые со связями (удовлетворяющие уравнениям связей), совершаемые в окрестности рассматриваемого положения системы при мгновенно остановленных («замороженных») связях (если они нестационарные). Символ « 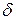» означает изохронную вариацию функции 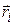(радиус-вектора 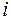- ой точки системы) – бесконечно малое приращение этой функции при фиксированном значении аргумента функции 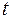. Вариация функции одной или нескольких переменных рассчитывается по тем же правилам, как и ее дифференциал, но при условии 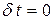. Виртуальные перемещения при стационарных связях называются также возможными.

Сумму элементарных работ задаваемых сил 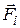на виртуальных (возможных) перемещениях точек механической системы будем называть виртуальной (возможной) работой задаваемых сил:

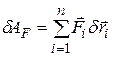. Виртуальная работа реакций связей 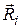есть величина 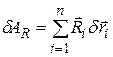, а виртуальная работа даламберовых сил инерции

.

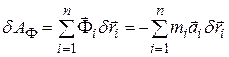Идеальные связи

Идеальными называют связи, реакции которых не совершают работу на виртуальных перемещениях точек системы, т.е. виртуальная работа реакций равна нулю при любом наборе из 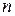векторов 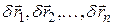(сокращенно обозначим последнее условие как ):

.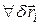
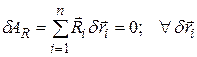